【2016常州一中夏令营Day5】

小 W 拼图
【问题描述】
小 W 和小 M 一起玩拼图游戏啦~
小 M 给小 M 一张 N 个点的图，有 M 条可选无向边，每条边有一个甜蜜值，小 W 要选K 条边，使得任意两点间最多有一条路径，并且选择的 K 条边甜蜜值之和最大。
【输入格式】
第一行三个正整数 N,M,K。
接下来 M 行，每行三个正整数 A,B,C，表示 A、B 两点间有一条甜蜜值为 C 的无向边。
【输出格式】
一行输出最大甜蜜值之和。
【输入输出样例】
carpet.in

5 4 3
1 2 10
1 3 9
2 3 7
4 5 3

carpet.out

22
【数据规模】
对于 20%的数据：K=1
对于 60%的数据：N,M<=1000，原图不含环
对于 100%的数据：N,M<=100000

题解

Kruskal最大生成树 当已添加边数=K时退出即可

#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;

int n,m,k,ans,cnt;
struct hh
{
    int a,b,w;
};
hh e[100005];
int f[100005];
bool cmp(hh a,hh b){return a.w>b.w;}
int find(int x){return f[x]==x?x:f[x]=find(f[x]);}

int main()
{
    int i,j,fx,fy;
    freopen("carpet.in","r",stdin);
    freopen("carpet.out","w",stdout);
    scanf("%d%d%d",&n,&m,&k);
    for(i=1;i<=m;i++) scanf("%d%d%d",&e[i].a,&e[i].b,&e[i].w);
    sort(e+1,e+m+1,cmp);
    for(i=1;i<=n;i++) f[i]=i;
    for(i=1;i<=m;i++)
    {
        fx=find(e[i].a);
        fy=find(e[i].b);
        if(fx!=fy)
        {
            f[fx]=fy;
            ans+=e[i].w;
            cnt++;
        }
        if(cnt==k) break;
    }
    printf("%d",ans);
    fclose(stdin);
    fclose(stdout);
    return 0;
}

小 M 求和
【问题描述】
小 W 顺利地完成了拼图，该他给小 M 出题啦。
小 W 定义“！”运算符：
1、 N!k = N!(k-1) * (N-1)!k (N> 0 aNd k > 0)
2、 N!k = 1 (N = 0)
3、 N!k = N (k = 0)
现在小 W 告诉小 M N 和 k，小 M 需要说出 N!k 的不同约数个数。
为了降低难度，答案对 1000000009 取模就好了。
【输入格式】
第一行两个整数 N,M。
【输出格式】
一行一个整数，为答案。
【输入输出样例】
calc.in
3 1
calc.out
4

calc.in
100 2
calc.out
321266186

【数据规模】
对于 30%的数据：N<=10,k<=10
对于 100%的数据：N<=1000,k<=100

题解

表示 则

易得 其中

规律比较明显，因为指数满足组合数的性质。

然后把分解质因数,将 写成这样的形式

约数个数即为

#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
using namespace std;
long long  f[1005][105][205];
int n,k,cnt;
int p[1005];
bool b[1005];
long long ans;
int work(int i,int k)
{
    int pre=0;
    while(k>=i&&!(k%i))
    {
        pre++;
        k=k/i;
    }
    return pre;
}
int main()
{
    int i,j,k,l;
    freopen("calc.in","r",stdin);
    freopen("calc.out","w",stdout);
       for(i=2;i<=1000;i++)
       {
            if(!b[i])p[++cnt]=i;
         for(j=1;j<=cnt&&i*p[j]<=1000;j++) b[i*p[j]]=true;
       }
    scanf("%d%d",&n,&k);
    for(i=1;i<=n;i++)
          for(j=1;j<=cnt;j++)
               if(i>=p[j]) f[i][0][j]=work(p[j],i);
    for(i=1;i<=n;i++)
          for(j=1;j<=k;j++)
            for (l=1;l<=cnt;l++)
                 f[i][j][l]=(f[i-1][j][l]+f[i][j-1][l])%1000000009;
    ans=1;
    for(i=1;i<=cnt;i++)
          ans=(ans*(long long)(f[n][k][i]+1)%1000000009);
    printf("%lld",ans);
    fclose(stdin);
    fclose(stdout);
    return 0;
}

小 W 旅游
【问题描述】
小 W 和小 M 正在出国旅游中~
他们到的国家共有 n 个城市，由 m 条分别属于 c 家公司的双向路连接。

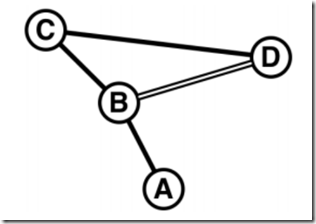
上图是路线图的一个例子。假设要从车站 A 到车站 D，最短的路线显然是 A → B → D。然而，最短的路线并不意味着最便宜的路线。上图中，铁路 A − B, B − C, C − D 属于同一家铁路公司，而铁路 B − D 属于另一家铁路公司，那么此时路线 A → B → C → D 就
可能比路线 A → B → D 便宜。这其中的主要原因，就是连续一段属于同一家铁路公司的路线花费并不与长度成正比，通常长度越长单位长度的花费就越少。那么，最终的路线可以被分为若干段，每段都属于同一家铁路公司，总花费就是每段花费之和。
现在小 W 想知道从 s 城市到 t 城市的最小花费，请问你能帮帮他吗？
【输入格式】

【输出格式】
若存在从 s 到 t 的路线，则第一行包含一个整数，表示最小花费；否则第一行包含一
个整数 −1。
第 5 页 共 5 页
【输入输出样例】

railway.in
4 4 2 1 4
1 2 2 1
2 3 2 1
3 4 5 1
2 4 4 2
3 2
3 6
10 5 3
100
10 9

railway.out
54

【数据规模】
对于 30%的数据：n=2
对于 60%的数据：c=1
对于 100%的数据：2≤n≤100，0≤m≤ 10^4，1≤c≤20，s ≠ t，xi ≠yi，1 ≤zi≤200，1≤pj≤50，1≤qj,k≤10^4，1≤rj,k≤100

题解

先用Floyd暴力跑出对于每个公司地铁 任意点间的最短路 以及花费

用花费暴力建边最后再跑一边最短路即可

#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;

int n,m,c,s,t,num,ans;
int dis[105][105];
int p[105],q[105][105],r[105][105],g[105][105][105];

int work(int d,int x)
{
    int i,j,k,h,hh,pre,y,z,now,t;
    if(d==0) return 0;
    if(d>=9999999) return d;
    pre=p[x];
    for(i=p[x];i>=0;i--)
      if(q[x][i]<d)
      {
          pre=i;
          break;
      }
    now=t=0;
    for(i=1;i<=pre;i++)
    {
        t+=(q[x][i]-now)*r[x][i];
        now=q[x][i];
    }
    t+=(d-now)*r[x][pre+1];
    return t;
}

void floyd()
{
    int i,j,k,x;
    for(x=1;x<=c;x++)
     for(k=1;k<=n;k++)
      for(i=1;i<=n;i++)
       for(j=1;j<=n;j++)
        if(g[x][i][j]>g[x][i][k]+g[x][k][j])
         g[x][i][j]=g[x][i][k]+g[x][k][j];
    return;
}
int main()
{
    int i,j,k,x,y,z,h,d,pre,now;
    freopen("railway.in","r",stdin);
    freopen("railway.out","w",stdout);
    scanf("%d%d%d%d%d",&n,&m,&c,&s,&t);
    for(i=1;i<=n;i++)
     for(j=1;j<=n;j++)
      for(k=1;k<=c;k++)
      if(j!=i) g[k][i][j]=dis[i][j]=9999999;

    for(i=1;i<=m;i++)
    {
        scanf("%d%d%d%d",&x,&y,&z,&h);
        g[h][x][y]=z;
        g[h][y][x]=z;
    }
    for(i=1;i<=c;i++) scanf("%d",&p[i]);
    for(i=1;i<=c;i++)
    {
        for(j=1;j<=p[i]-1;j++) scanf("%d",&q[i][j]); q[i][p[i]]=9999999;
        for(j=1;j<=p[i];j++) scanf("%d",&r[i][j]);
    }
    floyd();
    for(x=1;x<=c;x++)
    {
        for(i=1;i<=n;i++)
         for(j=1;j<=n;j++)
         {
             d=g[x][i][j];
             now=work(d,x);
             if(now<dis[i][j]) dis[i][j]=now;
         }
    }
    for(k=1;k<=n;k++)
     for(i=1;i<=n;i++)
      for(j=1;j<=n;j++)
          if(dis[i][j]>dis[i][k]+dis[k][j]) dis[i][j]=dis[i][k]+dis[k][j];

    printf("%d",dis[s][t]);
    fclose(stdin);
    fclose(stdout);
    return 0;
}