广度优先搜索 BFS算法

---

广度优先搜索算法（Breadth-First-Search，BFS），又称作宽度优先搜索。BFS算法是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。

算法思想

1、首先将根节点放入队列中。

2、从队列中取出第一个节点，并检验它是否为目标。

• 如果找到目标，则结束搜索并回传结果。
• 否则将它所有尚未检验过的直接子节点加入队列中。

3、若队列为空，表示整张图都检查过了——亦即图中没有欲搜索的目标。结束搜索并回传“找不到目标”。

4、重复步骤2。

搜索过程演示

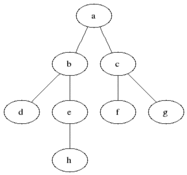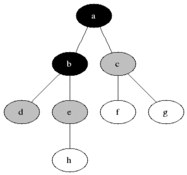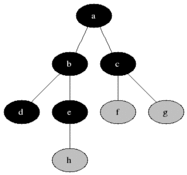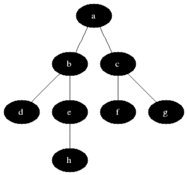
说明

• 灰色的是加入队列中的活动节点，黑色是从活动节点队列中选取的扩展节点。

• 每次将一个活动节点标记为扩展节点后，进行判断，并将该点从活动节点队列中移除，再将该节点所有未检测的子节点加入活动节点队列中去。

• 接下来再从队列中选取新的活动节点作为扩展节点，如此循环下去，直至队列为空为止，说明已经遍历过所有的节点。

复杂度

• 因为所有节点都必须被存储，因此BFS的空间复杂度为 O(|V|+|E|)，其中 |V| 是节点的数目，而 |E| 是图中边的数目。

• 最差情形下，BFS必须查找所有到可能节点的所有路径，因此其时间复杂度为 O(|V|+|E|)。

C++实现

//Given a binary tree, find its minimum depth.
//The minimum depth is the number of nodes along
//the shortest path from the root node down to
//the nearest leaf node.
// 递归方法
class Solution
{
public:
	int run(TreeNode *root)
         {
		if (!root)
		{
			return 0;
		}
		// 若左子树为空，返回右子树深度 + 1
		if (root->left == nullptr)
		{
			return (run(root->right) + 1);
		}
		// 若右子树为空，返回左子树深度 + 1
		if (root->right == nullptr)
		{
			return (run(root->left) + 1);
		}
		// 左右子树都不为空，返回较小值
		int leftDepth = run(root->left);
		int rightDepth = run(root->right);
		return ((leftDepth < rightDepth) ? (leftDepth + 1) : (rightDepth + 1));
	}
};
// BFS方法
#include <vector>
using namespace std;
class Solution
{
public:
	int run(TreeNode *root)
         {
		if (!root)
		{
			return 0;
		}
		vector <TreeNode *> que;
		TreeNode *now = root;  // 当前访问的节点
		TreeNode *last = root;  // 每层最后的一个节点
		que.push_back(root);
		int depth = 1;  // 初始深度
		while (que.size())
		{
			// 取出队列中的第一个节点作为当前节点
			now = que.front();
			que.erase(que.begin());
			// 如果当前节点没有子节点了，直接终止循环，说明是叶子节点，返回最小深度
			if ((now->left == nullptr) && (now->right == nullptr))
			{
				break;
			}
			// 将子节点加入队列中
			if (now->left != nullptr)
			{
				que.push_back(now->left);
			}
			if (now->right != nullptr)
			{
				que.push_back(now->right);
			}
			// 当访问到每层的最后一个节点时，深度+1
			if (now == last)
			{
				depth++;
				last = que.back();  // 将下一层最后一个节点赋给last
			}
		}
		return depth;
	}
};

BFS在迷宫问题的应用

• MTK编程挑战赛决赛《算术迷宫》

---

References

• 深度优先搜索 - 维基百科，自由的百科全书
• 算法入门 广度/宽度优先搜索(BFS) - CSDN博客
• Algorithms: Graph Search, DFS and BFS - YouTube

---