ACM数据结构-并查集

ACM数据结构-并查集

---

 

　　并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中，其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在比赛规定的运行时间（1～3秒）内计算出试题需要的结果，只能用并查集来描述。

　　并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。

主要操作

初始化

把每个点所在集合初始化为其自身。

通常来说，这个步骤在每次使用该数据结构时只需要执行一次，无论何种实现方式，时间复杂度均为O(N)。

查找

查找元素所在的集合，即根节点。

合并

将两个元素所在的集合合并为一个集合。

通常来说，合并之前，应先判断两个元素是否属于同一集合，这可用上面的“查找”操作实现。

---

部分代码如下：

构造并查集初始化

const int MAXSIZE = 100005;

int pre[MAXSIZE];

void makeSet(int size)
{
    for(int i=0;i<size;i++)
        pre[i]=i;
}

接下来find操作

int find(int x)
{
    int r=x;
    while(r!=pre[r])
        r=pre[r];
    return r;
}

void Merge(int x,int y)
{
    int fx=find(x);
    int fy=find(y);
    if(fx!=fy)
        pre[fx]=fy;
}

如果每次都沿着父节点向上查找，那时间复杂度就是树的高度，完全不可能达到常数级。这里需要应用一种非常简单而有效的策略——路径压缩。

路径压缩，就是在每次查找时，令查找路径上的每个节点都直接指向根节点，如图所示：

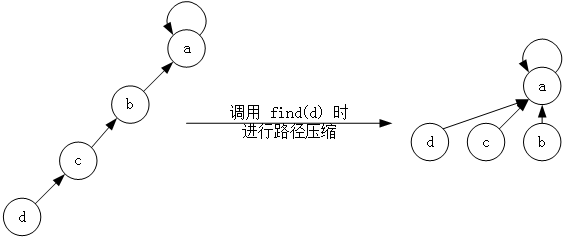
下面是两个版本的find操作：

 int find(int x)
 {
     if(x!=pre[x])
         pre[x]=find(pre[x]);
     return pre[x];
 }

递归版

 int find(int x)
 {
     int r=x , t;
     while(pre[r]!=r)
         r=pre[r];        //返回根节点
     while(r!=x)         //路径压缩
     {
         t=pre[x];
         pre[x]=r;
         x=t;
     }
     return x;
 }

非递归版

最后是合并操作 unionSet，并查集的合并也非常简单，就是将一个集合的树根指向另一个集合的树根，如图 所示。

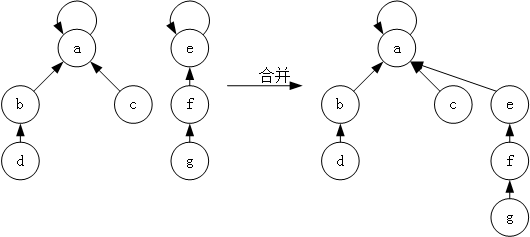
这里也可以应用一个简单的启发式策略——按秩合并。该方法使用秩来表示树高度的上界，在合并时，总是将具有较小秩的树根指向具有较大秩的树根。简单的说，就是总是将比较矮的树作为子树，添加到较高的树中。为了保存秩，需要额外使用一个与 pre 同长度的数组，并将所有元素都初始化为 0。

void unionSet(int x,int y)
{
    int fx=find(x);
    int fy=find(y);
    if(fx==fy)
        return ;
    if(rank[fx]>rank[fy])
        pre[fy]=fx;
    else
    {
        pre[fx]=fy;
        if(rank[fx]==rank[fy])
            rank[fy]++;
    }
}

除了按秩合并，并查集还有一种常见的策略，就是按集合中包含的元素个数（或者说树中的节点数）合并，将包含节点较少的树根，指向包含节点较多的树根。这个策略与按秩合并的策略类似，同样可以提升并查集的运行速度，而且省去了额外的 rank 数组。

这样的并查集具有一个略微不同的定义，即若 uset 的值是正数，则表示该元素的父节点（的索引）；若是负数，则表示该元素是所在集合的代表（即树根），而且值的相反数即为集合中的元素个数。相应的代码如下所示，同样包含递归和非递归的 find 操作：

const int MAXSIZE = 1000005;

int pre[MAXSIZE];

void makeSet(int size)
{
    for(int i = 0;i < size;i++)
        pre[i] = -1;
}

int find(int x)
{
    if (pre[x] < 0)
        return x;
    pre[x] = find(pre[x]);
    return pre[x];
}

int find(int x)
{
    int r = x, t;
    while (pre[r] >= 0)
        r = pre[r];
    while (x != r)
    {
        t = pre[x];
        pre[x] = r;
        x = t;
    }
    return x;
}

void unionSet(int x, int y)
{
    int fx = find(x);
    int fy = find(y);
    if (fx==fy)
        return;
    if (pre[fx] < pre[fy])
    {
        pre[fx] += pre[fy];
        pre[fy] = fx;
    }
    else
    {
        pre[fy] += pre[fx];
        pre[fx] = fy;
    }
}

如果要获取某个元素 x 所在集合包含的元素个数，可以使用 -pre[find(x)] 得到。