洛谷P3620 [APIO/CTSC 2007] 数据备份 [堆，贪心，差分]

　　题目传送门

　　

题目描述

你在一家 IT 公司为大型写字楼或办公楼(offices)的计算机数据做备份。然而数据备份的工作是枯燥乏味的，因此你想设计一个系统让不同的办公楼彼此之间互相备份，而你则坐在家中尽享计算机游戏的乐趣。

已知办公楼都位于同一条街上。你决定给这些办公楼配对(两个一组)。每一对办公楼可以通过在这两个建筑物之间铺设网络电缆使得它们可以互相备份。

然而，网络电缆的费用很高。当地电信公司仅能为你提供 K 条网络电缆，这意味着你仅能为 K 对办公楼(或总计 2K 个办公楼)安排备份。任一个办公楼都属于唯一的配对组(换句话说，这 2K 个办公楼一定是相异的)。

此外，电信公司需按网络电缆的长度(公里数)收费。因而，你需要选择这 K对办公楼使得电缆的总长度尽可能短。换句话说，你需要选择这 K 对办公楼，使得每一对办公楼之间的距离之和(总距离)尽可能小。

下面给出一个示例，假定你有 5 个客户，其办公楼都在一条街上，如下图所示。这 5 个办公楼分别位于距离大街起点 1km, 3km, 4km, 6km 和 12km 处。电信公司仅为你提供 K=2 条电缆。

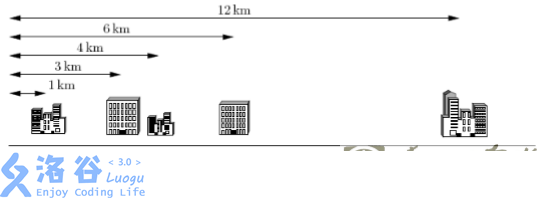
上例中最好的配对方案是将第 1 个和第 2 个办公楼相连，第 3 个和第 4 个办公楼相连。这样可按要求使用 K=2 条电缆。第 1 条电缆的长度是 3km―1km = 2km，第 2 条电缆的长度是 6km―4km = 2 km。这种配对方案需要总长 4km 的网络电缆，满足距离之和最小的要求。

输入输出格式

输入格式：

输入文件的第一行包含整数 n 和 k，其中 n(1≤n≤100 000)表示办公楼的数目，k(1≤k≤n/2)表示可利用的网络电缆的数目。

接下来的 n 行每行仅包含一个整数(0≤s≤1000 000 000), 表示每个办公楼到大街起点处的距离。这些整数将按照从小到大的顺序依次出现。

输出格式：

输出文件应当由一个正整数组成，给出将 2K 个相异的办公楼连成 K 对所需的网络电缆的最小总长度。

输入输出样例

输入样例#1： 复制

5 2
1
3
4
6
12 

输出样例#1： 复制

4

说明

30%的输入数据满足 n≤20。

60%的输入数据满足 n≤10 000

---

　　分析：易证，最优解中配对的大楼一定是相邻的，就可以将每两栋相邻的大楼之间的距离Di求出来，就可以将问题转化为:[有n-1个元素的数列Di，从中取出k个数，使得这k个数的和最小，并且相邻的数不能同时选]。

　　再从简单的情况开始分析：

　　如果k=1，那么直接选最小的元素。

　　如果k=2，那么要么选最小的元素D[i]和除了D[i-1],D[i],D[i+1]以外的最小的元素，要么选择D[i]两边的元素即D[i-1]和D[i+1]

　　那么由第二种情况就可以分析得到，对于当前数列中的元素，要么一定要选最小元素D[i]，要么就一定要选最小元素两边的元素D[i-1],D[i+1]。也就是说，最小元素左右两侧的元素要么同时被选，要么同时不选。。那么就可以先选出D[]中最小的元素D[i]，然后将D[i-1],D[i],D[i+1]从数列中删除，并在原位置插入一个新元素D[i-1]+D[i+1]-D[i]，然后重复操作即可。（因为如果在后面的操作中选择了D[i-1]+D[i+1]-D[i]这个元素，就相当于去掉已选择的结果中的D[i]换上D[i-1]+D[i+1]，如果后面没选该元素，则选择D[i]是一步最优策略）

　　那算法也就可以推导出了：建立一个链表L和一个小根堆H，L中有n-1个元素，每个元素与小根堆中的每一个元素成一一映射关系，它们的元素都是D[i]，也就是每两栋楼之间的距离。取出堆顶，将权值累加到答案上，再将堆顶x删除，同时将x的左右两侧的元素pre[x],nxt[x]删除，在同样的位置插入一个新元素p，p的权值D[p]=D[pre[x]]+D[nxt[x]]-D[x]，再在链表的对应位置中插入对应的节点p。重复k次即可。

　　不过实际操作的时候有很多细节要注意，具体细节看代码吧。

　　Code：

　　

#include<bits/stdc++.h>
#define Fi(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
const int N=2e5+;
int n,k,size,heap[N],fheap[N];
int num[N],nxt[N],pre[N],ans;
inline int read()
{
  char ch=getchar();int num=;bool flag=false;
  while(ch<''||ch>''){if(ch=='-')flag=true;ch=getchar();}
  while(ch>=''&&ch<=''){num=num*+ch-'';ch=getchar();}
  return flag?-num:num;
}
inline void delet(int x)
{
  heap[x]=heap[size--];
  fheap[heap[size+]]=x;
  int ka=x;
  if(num[heap[ka]]>=num[heap[ka>>]]){
    int s=ka<<;
    while(s<=size){
      if(s<size&&num[heap[s+]]<num[heap[s]])s++;
      if(num[heap[ka]]>num[heap[s]]){
    swap(fheap[heap[ka]],fheap[heap[s]]);
    swap(heap[ka],heap[s]);ka=s;s=ka<<;}
      else break;}}
  else{while(ka>){if(num[heap[ka]]<num[heap[ka>>]]){
    swap(fheap[heap[ka]],fheap[heap[ka>>]]);
    swap(heap[ka],heap[ka>>]);ka>>=;}
      else break;}}
}
inline void insert(int x)
{
  heap[++size]=x;fheap[x]=size;int ka=size;
  while(ka>){
    if(num[heap[ka]]<num[heap[ka>>]])
      {swap(fheap[heap[ka]],fheap[heap[ka>>]]);
    swap(heap[ka],heap[ka>>]);ka>>=;}
    else break;}
}
int main()
{
  n=read();k=read();int x1,x2;
  x1=read();Fi(i,,n){
    nxt[i]=i+;pre[i]=i-;x2=read();
    num[i]=x2-x1;x1=x2;insert(i);}
  num[]=1e9+;num[++n]=1e9+;
  insert(),insert(n);
  Fi(i,,k){
    int x=heap[];delet();
    delet(fheap[pre[x]]);delet(fheap[nxt[x]]);
    int x1=num[pre[x]],x2=num[nxt[x]];
    num[++n]=x1+x2-num[x];
    pre[n]=pre[pre[x]];nxt[n]=nxt[nxt[x]];
    pre[nxt[n]]=n;nxt[pre[n]]=n;insert(n);
    ans+=num[x];}cout<<ans;return ;
}