hdu 1533(最小费用最大流)

Going Home

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 4223    Accepted Submission(s): 2178

Problem Description

On
a grid map there are n little men and n houses. In each unit time,
every little man can move one unit step, either horizontally, or
vertically, to an adjacent point. For each little man, you need to pay a
$1 travel fee for every step he moves, until he enters a house. The
task is complicated with the restriction that each house can accommodate
only one little man.

Your task is to compute the minimum amount
of money you need to pay in order to send these n little men into those
n different houses. The input is a map of the scenario, a '.' means an
empty space, an 'H' represents a house on that point, and am 'm'
indicates there is a little man on that point.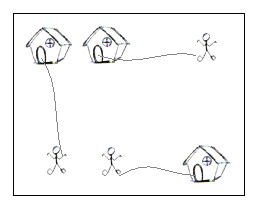

You
can think of each point on the grid map as a quite large square, so it
can hold n little men at the same time; also, it is okay if a little man
steps on a grid with a house without entering that house.

 

Input

There
are one or more test cases in the input. Each case starts with a line
giving two integers N and M, where N is the number of rows of the map,
and M is the number of columns. The rest of the input will be N lines
describing the map. You may assume both N and M are between 2 and 100,
inclusive. There will be the same number of 'H's and 'm's on the map;
and there will be at most 100 houses. Input will terminate with 0 0 for N
and M.

 

Output

For each test case, output one line with the single integer, which is the minimum amount, in dollars, you need to pay.

 

Sample Input

2 2
.m
H.
5 5
HH..m
.....
.....
.....
mm..H
7 8
...H....
...H....
...H....
mmmHmmmm
...H....
...H....
...H....
0 0

 

Sample Output

2
10
28

 

Source

Pacific Northwest 2004

 

题意:在一个n*m的矩阵里面有一些人和一些房屋,这些人都要到其中一个房屋里面去,一个人到一个房屋的费用为两者之间的曼哈顿距离,问所有的人和房子配对所需的最小花费?

题解:最小费用最大流模板题,也可以用KM算法,建图容量就是房屋和人之间的连一条为1的边，花费就是两者之间曼哈顿距离.建立源点和汇点，源点与人之间连一条容量1，费用0的边，房屋与汇点类似，跑一遍最小费用最大流即可。

#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
const int INF = ;
const int N = ; ///most 100 person and house
const int M = N*N*;
struct Edge{
    int u,v,cap,cost,next;
}edge[M];
int head[N],tot,low[N],pre[N];
int total ;
bool vis[N];
void addEdge(int u,int v,int cap,int cost,int &k){
    edge[k].u=u,edge[k].v=v,edge[k].cap = cap,edge[k].cost = cost,edge[k].next = head[u],head[u] = k++;
    edge[k].u=v,edge[k].v=u,edge[k].cap = ,edge[k].cost = -cost,edge[k].next = head[v],head[v] = k++;
}
void init(){
    memset(head,-,sizeof(head));
    tot = ;
}
bool spfa(int s,int t,int n){
    memset(vis,false,sizeof(vis));
    for(int i=;i<=n;i++){
        low[i] = (i==s)?:INF;
        pre[i] = -;
    }
    queue<int> q;
    q.push(s);
    while(!q.empty()){
        int u = q.front();
        q.pop();
        vis[u] = false;
        for(int k=head[u];k!=-;k=edge[k].next){
            int v = edge[k].v;
            if(edge[k].cap>&&low[v]>low[u]+edge[k].cost){
                low[v] = low[u] + edge[k].cost;
                pre[v] = k; ///v为终点对应的边
                if(!vis[v]){
                    vis[v] = true;
                    q.push(v);
                }
            }
        }
    }
    if(pre[t]==-) return false;
    return true;
}
int MCMF(int s,int t,int n){
    int mincost = ,minflow,flow=;
     while(spfa(s,t,n))
    {
        minflow=INF+;
        for(int i=pre[t];i!=-;i=pre[edge[i].u])
            minflow=min(minflow,edge[i].cap);
        flow+=minflow;
        for(int i=pre[t];i!=-;i=pre[edge[i].u])
        {
            edge[i].cap-=minflow;
            edge[i^].cap+=minflow;
        }
        mincost+=low[t]*minflow;
    }
    total=flow;
    return mincost;
}
int n,m,a,b;
char graph[N][N];
struct House{
    int x,y;
}h[N];
struct Person{
    int x,y;
}p[N];
int main()
{
    while(scanf("%d%d",&n,&m)!=EOF,n+m){
        init();
        a=,b=;
        for(int i=;i<n;i++){
            scanf("%s",graph[i]);
            for(int j=;j<m;j++){
                if(graph[i][j]=='H'){
                    h[++a].x = i,h[a].y = j;
                }
                if(graph[i][j]=='m'){
                    p[++b].x = i,p[b].y = j;
                }
            }
        }
        int src = ,des = a+b+;
        for(int i=;i<=a;i++){
            for(int j=;j<=b;j++){
                int D = abs(h[i].x-p[j].x)+abs(h[i].y-p[j].y);
                addEdge(i,j+a,,D,tot);
            }
        }
        for(int i=;i<=a;i++){
            addEdge(src,i,,,tot);
        }
        for(int i=;i<=b;i++){
            addEdge(i+a,des,,,tot);
        }
        int mincost = MCMF(src,des,a+b+);
        printf("%d\n",mincost);
    }
    return ;
}