[BZOJ4244]邮戳拉力赛

Description

IOI铁路是由N+2个站点构成的直线线路。这条线路的车站从某一端的车站开始顺次标号为0...N+1。

这条路线上行驶的电车分为上行电车和下行电车两种，上行电车沿编号增大方向行驶，下行电车沿编号减小方向行驶。乘坐这两种电车的话，移动1站的距离需要T秒。换句话说，乘坐上行电车从车站i走到车站i+1需要T秒，称作下行电车从车站i走到车站i-1也需要T秒。你不能在0号车站乘坐下行电车，或在N+1号车站乘坐上行电车。由于电车发车的频率非常高，你可以无视等待电车消耗的时间。

每个车站设有上行电车的站台和下行电车的站台，连接两个站台的道路上设有邮戳台。

现在，IOI铁路召开了邮戳拉力赛。在拉力赛中，选手需要从0号车站的上行电车站台出发，在1...N号车站各盖一枚邮戳，最终到达N+1号车站的上行电车站台即可完成。

为了在每个车站盖上邮戳，必须从电车上下来，步行走到车站通路上的邮戳台。在i号车站的上行电车站台、邮戳台、下行电车站台之间移动所消耗的时间如下所示：

从车站i的上行电车站台到邮戳台的时间为Ui秒

从车站i的邮戳台到上行电车站台的时间为Vi秒

从车站i的下行电车站台到邮戳台的时间为Di秒

从车站i的邮戳台到下行电车站台的时间为Ei秒

邮戳拉力赛的选手只能访问0号车站与N+1号车站各一次。1...N号车站都可以访问任意多次。

现在给出有邮戳台的车站个数、乘坐电车移动一站的时间、在每个车站的上行电车站台、邮戳台、下行电车站台之间移动所消耗的时间，请你求出完成邮戳拉力赛的最短时间。

这个时间包括从0号车站出发，按下N个邮戳后到达N+1号车站的时间。无视等车的时间和按邮戳的时间。

Input

第一行两个空格分隔的整数N和T，表示有N+2个车站，电车行驶一站的距离需要T秒

接下来N行，第i行有四个空格分隔的整数Ui,Vi,Di,Ei，分别表示：

从车站i的上行电车站台到邮戳台的时间为Ui秒

从车站i的邮戳台到上行电车站台的时间为Vi秒

从车站i的下行电车站台到邮戳台的时间为Di秒

从车站i的邮戳台到下行电车站台的时间为Ei秒

Output

输出一行一个整数，表示完成邮戳拉力赛的最短时间。

Sample Input

4 1
1 1 1 1
1 9 9 1
9 9 1 1
1 9 9 1

Sample Output

HINT

从车站0出发，按照2-1-4-3-1-5的顺序访问车站可以达到最短时间。

1<=N<=3000

1<=T<=10^5

1<=Ui<=10^5(1<=i<=N)

1<=Vi<=10^5(1<=i<=N)

1<=Di<=10^5(1<=i<=N)

1<=Ei<=10^5(1<=i<=N)

好几天没更博客了，最近做了一道很妙的背包题，记录一下

首先我们很容易发现，最后的路线一定是一条上行线走到头外加几个环

然后我们为了盖邮戳，一共有四种搞法：

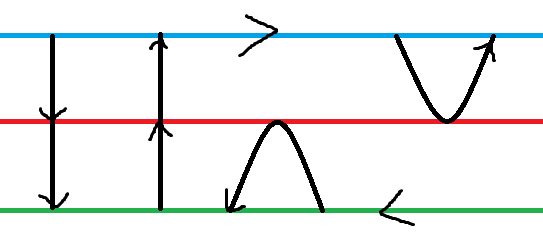
而且因为除了一条直线之外的全是环，所以如果存在$x$种第一种取法，就必定有$x$种第二种取法与之对应

而对于第三种和第四种取法，由于不会改变行走的方向，所以不用单独处理

这就可以对应到括号序列上来，第二种取法是左括号，第一种取法是右括号，这样对应的原因是你可以用二在后一在前来消除影响，但如果一在前就无法消除影响了，具体原因就是线路方向

然后还有需要注意的是，如果我们要用第三种取法，就要保证他之前有第二种取法的影响还未被消掉（你得保证此时的可以到达下行线）

所以我们设$f_{ij}$表示到$i$还剩$j$个左括号的时候最小代价是多少

按照上面四种情况转移即可

代码：

 #include<iostream>

 #include<cstdio>

 #include<cstring>

 using namespace std;

 int n,T;

 int f[][];

 int main() {

     memset(f,,sizeof(f)),f[][]=;

     scanf("%d%d",&n,&T);

     for(int i=;i<=n;i++) {

         int u,v,d,e;scanf("%d%d%d%d",&u,&v,&d,&e);

         for(int j=;j<=n;j++) f[i-][j]+=j*T*;

         //下->中->上

         for(int j=;j<=n;j++) f[i][j]=min(f[i][j],f[i-][j-]+d+v);

         //上->中->下

         for(int j=;j<n;j++) f[i][j]=min(f[i][j],f[i-][j+]+u+e);

         //上->中->上

         for(int j=;j<=n;j++) f[i][j]=min(f[i][j],f[i-][j]+u+v);

         //下->中->下

         for(int j=;j<=n;j++) f[i][j]=min(f[i][j],f[i-][j]+d+e);

         //消除上->中->下的影响

         for(int j=;j<=n;j++) f[i][j]=min(f[i][j],f[i][j-]+d+v);

         //消除下->中->上的影响

         for(int j=n-;j;j--) f[i][j]=min(f[i][j],f[i][j+]+u+e);

     }

     printf("%d\n",f[n][]+(n+)*T);

     return ;

 }