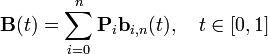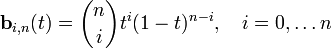贝塞尔曲线.简单推导与用opengl实现动态画出。
在opengl中,我们可以用少许的参数来描述一个曲线,其中贝塞尔曲线算是一种很常见的曲线控制方法,我们先来看维基百科里对贝塞尔曲线的说明:
线性贝塞尔曲线
给定点P0、P1,线性贝塞尔曲线只是一条两点之间的直线。这条线由下式给出:
且其等同于线性插值。
二次方贝塞尔曲线
二次方贝塞尔曲线的路径由给定点P0、P1、P2的函数B(t)追踪:
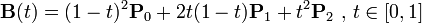 。
。
TrueType字体就运用了以贝塞尔样条组成的二次贝塞尔曲线。
一些关于参数曲线的术语,有
即多项式
又称作n阶的伯恩斯坦基底多项式,定义00 = 1。
点Pi称作贝塞尔曲线的控制点。多边形以带有线的贝塞尔点连接而成,起始于P0并以Pn终止,称作贝塞尔多边形(或控制多边形)。贝塞尔多边形的凸包(convex hull)包含有贝塞尔曲线。
在这里贴这些,是因为让我们有个基本的理解,下面把维基百科里一个动态图放上,让大家有更清晰了解贝塞尔曲线是如何生成的。



然后我们来分析相应数据的产生。最简单的二点,其实就是线段的参数化,大家能简单得到f(t)=p0+(p1-p0)*t=(1-t)p0+t*p1.
二次方贝塞尔曲线话,我直接用下面的图给出相应过程。

对应的三次方贝塞尔曲线,我们会如下图来门简略说明。
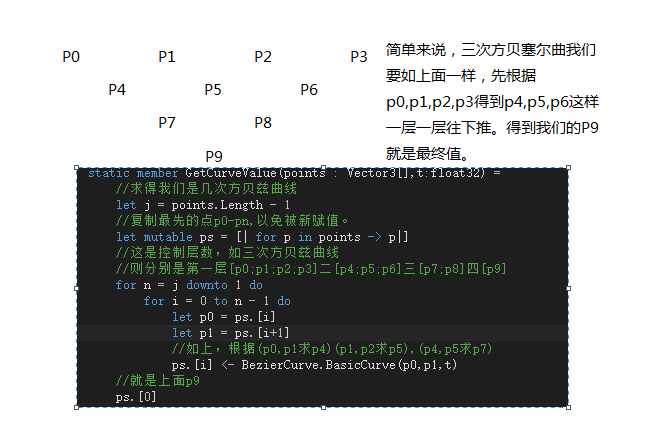
在上面,我们给出用我们推导的过程。下面是根据这个过程生成的主要代码。
type BezierCurve() =
static member BasicCurve (p0:Vector3, p1:Vector3,t) = (.f-t)*p0 + t*p1
static member GetCurveValue(points : Vector3[],t:float32) =
//求得我们是几次方贝兹曲线
let j = points.Length -
//复制最先的点p0-pn,以免被新赋值。
let mutable ps = [| for p in points -> p|]
//这是控制层数,如三次方贝兹曲线
//则分别是第一层[p0;p1;p2;p3]二[p4;p5;p6]三[p7;p8]四[p9]
for n = j downto do
for i = to n - do
let p0 = ps.[i]
let p1 = ps.[i+]
//如上,根据(p0,p1求p4)(p1,p2求p5),(p4,p5求p7)
ps.[i] <- BezierCurve.BasicCurve(p0,p1,t)
//就是上面p9
ps.[]
static member CreateCurve(points : Vector3[],count:int) =
let ps = Array.create count Vector3.Zero
let step = .f/float32 count
let len = count -
for i = to len do
ps.[i] <- BezierCurve.GetCurveValue(points,step * float32 i)
ps
static member GetCurveValueS(points : Vector3[],t:float32) =
let j = points.Length -
let mutable ps = [| for p in points -> p|]
let mutable rs = [||]
for n = j downto do
for i = to n - do
let p0 = ps.[i]
let p1 = ps.[i+]
ps.[i] <- BezierCurve.BasicCurve(p0,p1,t)
rs <- Array.append rs ps.[ .. n-]
ps.[],rs
BasicCurve就是我们线段的参数化,pt=p0+(p1-p0)*t=(1-t)p0+t*p1.
而GetCurveValue就是如上面所示,求多次方贝兹曲线在t(0<t<1)时的值。
而CreateCurve这个就是我们要生成的贝兹曲线在程序里的精度,值越高则画的点越多。看起来越逼真。
那下来,我们来生成如维基百科的那种动态图,也好加深的我们的印象。根据动态图,我们要知道的是,在t点,每一层相邻的二个点走到那了(也就是上面的GetCurveValueS的实现),这里给出主要的代码。
override v.OnRenderFrame(e) =
base.OnRenderFrame e
GL.Clear (ClearBufferMask.ColorBufferBit ||| ClearBufferMask.DepthBufferBit)
let mutable lookat = Matrix4.LookAt(caram.Eye,caram.Target,Vector3.UnitY)
GL.MatrixMode(MatrixMode.Modelview)
GL.LoadMatrix(&lookat) GL.Color3(Color.White)
GL.VertexPointer(,VertexPointerType.Float,,vs)
GL.DrawArrays(BeginMode.LineStrip,,vs.Length)
currentTime <- currentTime + e.Time
if currentTime > totalTime && frame < allFrame then
frame <- frame +
let currentStep =float32 frame/float32 allFrame
let v = BezierCurve.GetCurveValueS(vs,currentStep)
ac <- Array.append ac [|fst v|]
ps <- snd v
currentTime <- currentTime - totalTime
printfn "ac:%A" ps
let mutable step =
for i = vs.Length - downto do
if ps.Length > step + i then
let is = ps.[step .. step + i]
GL.VertexPointer(,VertexPointerType.Float,,is)
GL.DrawArrays(BeginMode.LineStrip,,is.Length)
step <- step + i +
printfn "is:%A" is
GL.Color3(Color.Red)
GL.VertexPointer(,VertexPointerType.Float,,ac)
GL.DrawArrays(BeginMode.LineStrip,,ac.Length)
v.SwapBuffers()
在上面,我们用totalTime控制显示的快慢,用allFrame控制我们要显示的精度。frame表示当前t点的情况。
相关效果图:

下面给出相关源代码的附件
其中EDSF移动镜头,小键盘上的+与-分别控制动画的速度,R键重新开始画曲线过程。
贝塞尔曲面在opengl有比较容易的实现用求值器,下面是根据opengl红皮书的一个例子改的,定义一个数组,排列顺序按v,u,z来,u表示行,v表示每列,z表示是Vector3,Vector4的几个顶点,如:
let vvs = [|
//-1.5;-1.5;4.0; -0.5;-1.5;2.0; 0.5;-1.5;-1.0; 1.5;-1.5;2.0
-1.5;-0.5;1.0; -0.5;-0.5;3.0; 0.5;-0.5;0.0; 1.5;-0.5;-1.0
-1.5;0.5;4.0; -0.5;0.5;0.0; 0.5;0.5;3.0; 1.5;0.5;4.0
-1.5;1.5;-2.0; -0.5;1.5;-2.0; 0.5;1.5;0.0; 1.5;1.5;-1.0
|]
//[3,4,3],组织如上面,三列四行,每行三点就是Vector3
//数组格式[v][u][z] 则GL.Map2(MapTarget.Map2Vertexz,0.,1.,z,u,0.,1.,u*z,v,vvs)
GL.Map2(MapTarget.Map2Vertex3,.,.,,,.,.,,,vvs)
GL.MapGrid2(,.,.,,.,.)
GL.EvalMesh2(MeshMode2.Line,,,,)
这个贝塞尔曲面表示在u方向4个控制点,z方向有3个控制点,u的精细度是10,意思是u方向的线都是由10个点组成,v的精细度是5,精细度越高,线越光滑。效果图如下:

最后向法国工程师皮埃尔·贝塞尔致敬。
贝塞尔曲线.简单推导与用opengl实现动态画出。的更多相关文章
- 利用贝塞尔曲线绘制(UIBezierPath)自定义iOS动态速度表,可以自定义刻度,刻度值,进度条样式
GitHub的Demo下载地址 使用UIBezierPath画图步骤: 创建一个UIBezierPath对象 调用-moveToPoint:设置初始线段的起点 添加线或者曲线去定义一个或者多个子路径 ...
- 贝塞尔曲线:原理、自定义贝塞尔曲线View、使用!!!
一.原理 转自:http://www.2cto.com/kf/201401/275838.html Android动画学习Demo(3) 沿着贝塞尔曲线移动的Property Animation Pr ...
- Android -- 贝塞尔曲线公式的推导和简单使用
1,最近看了几个不错的自定义view,发现里面都会涉及到贝塞尔曲线知识,深刻的了解到贝塞尔曲线是进阶自定义view的一座大山,so,今天先和大家来了解了解. 2,贝塞尔曲线作用十分广泛,简单举几个的栗 ...
- OpenGL超级宝典笔记——贝塞尔曲线和曲面(转)
http://my.oschina.net/sweetdark/blog/183721 参数方程表现形式 在中学的时候,我们都学习过直线的参数方程:y = kx + b;其中k表示斜率,b表示截距(即 ...
- OpenGL 实践之贝塞尔曲线绘制
说到贝塞尔曲线,大家肯定都不陌生,网上有很多关于介绍和理解贝塞尔曲线的优秀文章和动态图. 以下两个是比较经典的动图了. 二阶贝塞尔曲线: 三阶贝塞尔曲线: 由于在工作中经常要和贝塞尔曲线打交道,所以简 ...
- cocos2d-x 贝塞尔曲线的简单运用(CCBezierTo,CCBezierBy)
原文链接:http://blog.csdn.net/we000636/article/details/8616355 一.贝赛尔曲线简单介绍 贝塞尔曲线是应用于二维图形应用程序的数学曲线.曲线的定义有 ...
- Android -- 贝塞尔曲线公式的推导
1,最近看了几个不错的自定义view,发现里面都会涉及到贝塞尔曲线知识,深刻的了解到贝塞尔曲线是进阶自定义view的一座大山,so,今天先和大家来了解了解. 2,贝塞尔曲线作用十分广泛,简单举几个的栗 ...
- 贝塞尔曲线UIBezierPath简单使用
//常用属性 /* 1.CGPath: 将UIBezierPath类转换成CGPath 2.currentPoint: 当前path的位置,可以理解为path的终点 3.lineWidth: 线条宽度 ...
- canvas贝塞尔曲线
贝塞尔曲线 Bézier curve(贝塞尔曲线)是应用于二维图形应用程序的数学曲线. 曲线定义:起始点.终止点.控制点.通过调整控制点,贝塞尔曲线的形状会发生变化. 1962年,法国数学家Pierr ...
随机推荐
- Pycrypto与RSA密码技术笔记
密码与通信 密码技术是一门历史悠久的技术.信息传播离不开加密与解密.密码技术的用途主要源于两个方面,加密/解密和签名/验签 在信息传播中,通常有发送者,接受者和窃听者三个角色.假设发送者Master想 ...
- hdu 1217 Arbitrage (最小生成树)
题目:http://acm.hdu.edu.cn/showproblem.php?pid=1217 /************************************************* ...
- 菜鸟学Java(二十一)——如何更好的进行单元测试——JUnit
测试在软件生命周期中的重要性,不用我多说想必大家也都非常清楚.软件测试有很多分类,从测试的方法上可分为:黑盒测试.白盒测试.静态测试.动态测试等:从软件开发的过程分为:单元测试.集成测试.确认测试.验 ...
- 菜鸟学Java(六)——简单验证码生成(Java版)
验证码大家都知道,它的作用也不用我多说了吧.如果不太清楚请参见百度百科中的解释,一般验证码的生成就是随机产生字符(数字.字母或者汉字等),然后将这些生成的字符绘制成一张图片,再在图片上加上一些干扰元素 ...
- [Windows Azure] Adding Sign-On to Your Web Application Using Windows Azure AD
Adding Sign-On to Your Web Application Using Windows Azure AD 14 out of 19 rated this helpful - Rate ...
- linux Ctrl+z和Ctrl+c的区别
1.Ctrl+z 挂起进程,并不会结束,执行fg命令可以重新启动这个被挂起的命令. 2.Ctrl+c 终止进程
- MonoBehaviour类Invoke, Coroutine
异步函数 在一个方法执行时调用另一个方法.而被调用的方法或者其中的某些语句不是立刻执行,而是过一段时间后才执行. MonoBehaviour提供了两种异步方法 调用(Invoke) 协程(Corout ...
- 李洪强iOS经典面试题
李洪强iOS经典面试题 1. struct和class的区别 swift中,class是引用类型,struct是值类型.值类型在传递和赋值时将进行复制,而引用类型则只会使用引用对象的一个"指 ...
- DIOCP开源项目-DIOCP3直接发送对象,帮你处理粘包问题
该DEMO演示,如何在客户端与服务端之间直接传递TStream对象,让你专注于处理数据逻辑,可以忽略处理网络传输间粘包的问题. 上面由服务端向所有的客户端推送一个消息TMemoryStream对象(该 ...
- 【嵌入式】FS2410非操作系统外围资源测试
在刚接触FS2410时,其实这个测试也没有多大意义,但是对于以后来说,当一个产品做成功时,产品测试还是一个必须经过的一个阶段,所以这个流程还是有必要走一下! 在非操作系统下,主要进行RTC测试,按键测 ...