HDU 1890 - Robotic Sort - [splay][区间反转+删除根节点]

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1890

Time Limit: 6000/2000 MS (Java/Others)　　Memory Limit: 32768/32768 K (Java/Others)

Problem Description

Somewhere deep in the Czech Technical University buildings, there are laboratories for examining mechanical and electrical properties of various materials. In one of yesterday’s presentations, you have seen how was one of the laboratories changed into a new multimedia lab. But there are still others, serving to their original purposes.

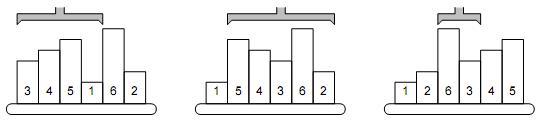
In this task, you are to write software for a robot that handles samples in such a laboratory. Imagine there are material samples lined up on a running belt. The samples have different heights, which may cause troubles to the next processing unit. To eliminate such troubles, we need to sort the samples by their height into the ascending order.

Reordering is done by a mechanical robot arm, which is able to pick up any number of consecutive samples and turn them round, such that their mutual order is reversed. In other words, one robot operation can reverse the order of samples on positions between A and B.

A possible way to sort the samples is to find the position of the smallest one (P1) and reverse the order between positions 1 and P1, which causes the smallest sample to become first. Then we find the second one on position P and reverse the order between 2 and P2. Then the third sample is located etc.

The picture shows a simple example of 6 samples. The smallest one is on the 4th position, therefore, the robot arm reverses the first 4 samples. The second smallest sample is the last one, so the next robot operation will reverse the order of five samples on positions 2–6. The third step will be to reverse the samples 3–4, etc.

Your task is to find the correct sequence of reversal operations that will sort the samples using the above algorithm. If there are more samples with the same height, their mutual order must be preserved: the one that was given first in the initial order must be placed before the others in the final order too.

 

Input

The input consists of several scenarios. Each scenario is described by two lines. The first line contains one integer number N , the number of samples, 1 ≤ N ≤ 100 000. The second line lists exactly N space-separated positive integers, they specify the heights of individual samples and their initial order.

The last scenario is followed by a line containing zero.

 

Output

For each scenario, output one line with exactly N integers P1 , P1 , . . . PN ,separated by a space.
Each Pi must be an integer (1 ≤ Pi ≤ N ) giving the position of the i-th sample just before the i-th reversal operation.

Note that if a sample is already on its correct position Pi , you should output the number Pi anyway, indicating that the “interval between Pi and Pi ” (a single sample) should be reversed.

 

Sample Input

6

3 4 5 1 6 2

4

3 3 2 1

0

 

Sample Output

4 6 4 5 6 6

4 2 4 4

题意：

给出一个n，给出n个样品的高度，

给出一种根据高度排序的算法，其第 i 次操作：找到第 i 小的那个数的位置为Pi，将整个区间[i,Pi]反转，这样一来第 i 小的数就在位置 i 上；从 i 等于 1 到 n 循环这样的操作。

现在要求你给出每次操作的Pi。

题解：

伸展树1~n建树，把每个节点key值等于节点的编号（即key[x] = x），同时使得中序遍历伸展树得到的序列为1~n，

以题目中两个样例为例，建成的树应为如下图：

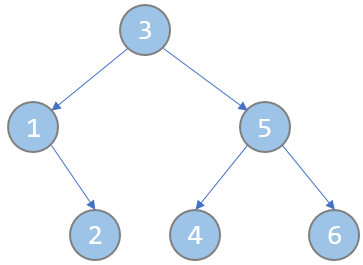
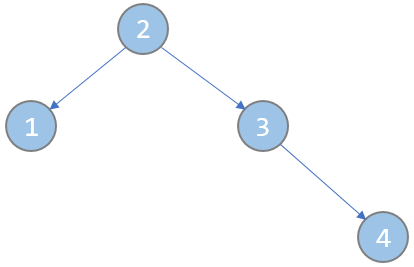　　　（注意，图中节点内的数字，既是节点编号，也是key值，即key[3] = 3，key[1] = 1，key[5] = 5……）

我们此时的伸展树维护的是n个样品的编号（编号为1~n）；

将n个样品按输入顺序编号，再按照first高度second编号进行升序排序，那么新的顺序，就是题目中所描述的排序算法中的每次操作的顺序，

这样，按新的顺序依次枚举n个样品，对于第 i 个样品，其编号为sample[i].id，

我们此时就要去伸展树中寻找某个节点x，其key[x] = sample[i].id；而我们要求的Pi，就是比这个节点小的节点个数加1；

根据上面反复提到的，key[x] = x，所以我们其实就是把节点x = sample[i].id伸展到根，然后求其左子树内节点个数，再加1，

同时，因为需要区间翻转，所以我们可以翻转左子树，并且删除根节点，相当于翻转了[i,Pi]，

由于我们不断的删除节点，因此实际答案就应该是左子树内节点个数 + 1 + (i - 1)。

AC代码：

#include<bits/stdc++.h>
#define Key_value ch[ch[root][1]][0]
using namespace std;
const int maxn=1e5+;

int n;
struct Sample
{
    int h;
    int id;
}sample[maxn];
bool cmp(Sample a,Sample b)
{
    if(a.h==b.h) return a.id<b.id;
    else return a.h<b.h;
}

/******************************** splay - st ********************************/
int root,nodecnt;
int par[maxn],ch[maxn][];
int key[maxn],size[maxn];
bool rev[maxn];
void NewNode(int &x,int p,int k)
{
    x=k;
    par[x]=p;
    ch[x][]=ch[x][]=;
    key[x]=k;
    size[x]=;
    rev[x]=;
}
void Update_Rev(int x)
{
    if(x==) return;
    rev[x]^=1;
}
void Pushup(int x)
{
    size[x]=size[ch[x][]]+size[ch[x][]]+;
}
void Pushdown(int x)
{
    if(rev[x])
    {
        swap(ch[x][],ch[x][]);
        Update_Rev(ch[x][0]);
        Update_Rev(ch[x][1]);
        rev[x]=;
    }
}
void Rotate(int x,int type) //旋转，0为左旋zag，1为右旋zig
{
    int y=par[x];
    Pushdown(y); Pushdown(x); //先把y的标记向下传递,再把x的标记往下传递
    ch[y][!type]=ch[x][type]; par[ch[x][type]]=y;
    if(par[y]) ch[par[y]][(ch[par[y]][]==y)]=x;
    par[x]=par[y];
    ch[x][type]=y; par[y]=x;
    Pushup(y); Pushup(x);
}
void Splay(int x,int goal)
{
    Pushdown(x);
    while(par[x]!=goal)
    {
        if(par[par[x]]==goal)
        {
            Pushdown(par[x]); Pushdown(x);
            Rotate(x,ch[par[x]][]==x); //左孩子zig，有孩子zag
        }
        else
        {
            Pushdown(par[par[x]]); Pushdown(par[x]); Pushdown(x);
            int y=par[x];
            int type=(ch[par[y]][]==y); //type=0，y是右孩子；type=1，y是左孩子
            if(ch[y][type]==x)
            {
                Rotate(x,!type);
                Rotate(x,type);
            }
            else
            {
                Rotate(y,type);
                Rotate(x,type);
            }
        }
    }
    if(goal==) root=x;
}
int Get_Kth(int x,int k) //得到第k个节点
{
    Pushdown(x);
    int t=size[ch[x][]]+;
    if(t==k) return x;
    if(t>k) return Get_Kth(ch[x][],k);
    else return Get_Kth(ch[x][],k-t);
}
int Get_Min(int x)
{
    Pushdown(x);
    while(ch[x][])
    {
        x=ch[x][];
        Pushdown(x);
    }
    return x;
}
int Get_Max(int x)
{
    Pushdown(x);
    while(ch[x][])
    {
        x=ch[x][];
        Pushdown(x);
    }
    return x;
}
void Build(int &x,int l,int r,int par)
{
    if(l>r) return;
    int mid=(l+r)/;
    NewNode(x,par,mid);
    Build(ch[x][],l,mid-,x);
    Build(ch[x][],mid+,r,x);
    Pushup(x);
}
void Init()
{
    root=nodecnt=;
    ch[root][]=ch[root][]=size[root]=key[root]=par[root]=rev[root]=;
    Build(root,,n,);
}
void Del()
{
    if(ch[root][]== && ch[root][]==) root=;
    else if(ch[root][]==)
    {
        par[ch[root][]]=;
        root=ch[root][];
    }
    else if(ch[root][]==)
    {
        par[ch[root][]]=;
        root=ch[root][];
    }
    else
    {
        int pre=Get_Max(ch[root][]);
        int nxt=Get_Min(ch[root][]);
        Splay(pre,); Splay(nxt,root);
        par[Key_value]=;
        Key_value=;
        Pushup(ch[root][]);
        Pushup(root);
    }
}
/******************************** splay - ed ********************************/

int main()
{
    while(scanf("%d",&n) && n!=)
    {
        Init();
        for(int i=;i<=n;i++)
        {
            scanf("%d",&sample[i].h);
            sample[i].id=i;
        }
        sort(sample+,sample+n+,cmp);

        for(int i=;i<n;i++)
        {
            Splay(sample[i].id,);
            printf("%d ",i+size[ch[root][]]);
            Update_Rev(ch[root][]);
            Del();
        }
        printf("%d\n",n);
    }
}