特征值分解，奇异值分解（SVD）

特征值分解和奇异值分解在机器学习领域都是属于满地可见的方法。两者有着很紧密的关系，我在接下来会谈到，特征值分解和奇异值分解的目的都是一样，就是提取出一个矩阵最重要的特征。

1. 特征值：

如果说一个向量v是方阵A的特征向量，将一定可以表示成下面的形式：

写成矩阵形式：

这时候λ就被称为特征向量v对应的特征值，一个矩阵的一组特征向量是一组正交向量。

2. 特征分解：

特征值分解是将一个矩阵分解成下面的形式：

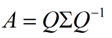
其中Q是这个矩阵A的特征向量组成的矩阵，正交矩阵是可逆的。Σ = diag(λ₁, λ₂, ..., λ_n)是一个对角阵，每一个对角线上的元素就是一个特征值。

首先，要明确的是，一个矩阵其实就是一个线性变换，因为一个矩阵乘以一个向量后得到的向量，其实就相当于将这个向量进行了线性变换。

　　当矩阵是高维的情况下，那么这个矩阵就是高维空间下的一个线性变换，这个线性变化可能没法通过图片来表示，但是可以想象，这个变换也同样有很多的变换方向，我们通过特征值分解得到的前N个特征向量，那么就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向，就可以近似这个矩阵（变换）。也就是之前说的：提取这个矩阵最重要的特征。总结一下，特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么，可以将每一个特征向量理解为一个线性的子空间，我们可以利用这些线性的子空间干很多的事情。

　　不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵。

3. 奇异值分解

　　特征值分解是一个提取矩阵特征很不错的方法，但是它只适用于方阵。而在现实的世界中，我们看到的大部分矩阵都不是方阵，比如说有M个学生，每个学生有N科成绩，这样形成的一个M * N的矩阵就可能不是方阵，我们怎样才能像描述特征值一样描述这样一般矩阵呢的重要特征呢？奇异值分解就是用来干这个事的，奇异值分解是一个能适用于任意的矩阵的一种分解的方法。

奇异值分解是一个能适用于任意的矩阵的一种分解的方法：

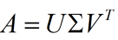    假设A是一个M * N的矩阵，那么得到的U是一个M * M的方阵（里面的向量是正交的，U里面的向量称为左奇异向量），Σ是一个M * N的实数对角矩阵（对角线以外的元素都是0，对角线上的元素称为奇异值），V^T(V的转置)是一个N * N的矩阵，里面的向量也是正交的，V里面的向量称为右奇异向量），从图片来反映几个相乘的矩阵的大小可得下面的图片

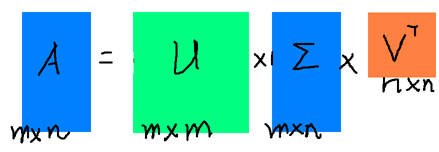
那么奇异值和特征值是怎么对应起来的呢？首先，我们将一个矩阵A的转置 A^T * A，将会得到 A^TA 是一个方阵，我们用这个方阵求特征值可以得到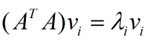：    这里得到的v，就是我们上面的右奇异向量。此外我们还可以得到：

这里的σ_i 就是就是上面说的奇异值，u_i就是上面说的左奇异向量。

常见的做法是将奇异值由大而小排列。如此Σ便能由M唯一确定了。

　　奇异值σ跟特征值类似，在矩阵Σ中也是从大到小排列，而且σ的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前r大的奇异值来近似描述矩阵，这里定义一下部分奇异值分解：

r是一个远小于m、n的数，这样矩阵的乘法看起来像是下面的样子：

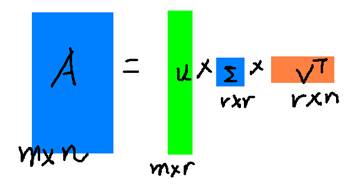
右边的三个矩阵相乘的结果将会是一个接近于A的矩阵，在这儿，r越接近于n，则相乘的结果越接近于A。而这三个矩阵的面积之和（在存储观点来说，矩阵面积越小，存储量就越小）要远远小于原始的矩阵A，我们如果想要压缩空间来表示原矩阵A，我们存下这里的三个矩阵：U、Σ、V就好了。

参考：

机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用