初识prufer序列

前言

\(prufer\)序列应该是一个比较实用的东西。

据\(hl666\)大佬说，一切与度数有关的树上计数问题，都可以用它以及它的性质来解决。

而听说\(ZJOI\)最近特别喜欢出计数题，所以有必要学一学。

转化\(1\)：从无根树到\(prefur\)序列

现在，给你一棵树，我们要考虑如何把它变成\(prefur\)序列。

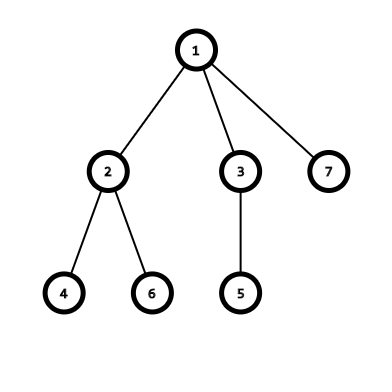
我们需要重复进行以下操作，直至树中只剩下两个点：

• 找到一个度数为\(1\)，且编号最小的点。（其中编号最小保证了后面将会提到的\(prufer\)序列的唯一对应性，同时也方便从\(prufer\)序列转化回无根树）
• 把这个点的父亲节点加入序列，然后把这个点从树中删除。

然后我们就得到了一个长度为\(n-2\)的序列，这就是\(prufer\)序列。

所以它有什么实际意义呢？

我也不知道。

以上面的图为例，我们可以模拟这一过程如下：

• 找到\(4\)号节点，将其父结点加入序列，然后将其删去。此时序列：\(\{2\}\)。
• 找到\(5\)号节点，将其父结点加入序列，然后将其删去。此时序列：\(\{2,3\}\)。
• 找到\(3\)号节点，将其父结点加入序列，然后将其删去。此时序列：\(\{2,3,1\}\)。
• 找到\(6\)号节点，将其父结点加入序列，然后将其删去。此时序列：\(\{2,3,1,2\}\)。
• 找到\(2\)号节点，将其父结点加入序列，然后将其删去。此时序列：\(\{2,3,1,2,1\}\)。

所以，最后得到的\(prufer\)序列就是\(\{2,3,1,2,1\}\)。

转化\(2\)：从\(prufer\)序列到无根树

还是以刚才那棵树为例吧，我们要考虑如何把它的\(prefur\)序列变回它本身。

我们需要重复进行以下操作，直至点集中只剩下两个点：（初始化所有点都在点集中）

• 取出\(prufer\)序列最前面的元素\(x\)。
• 取出在点集中的、且当前不在\(prufer\)序列中的最小元素\(y\)。（这恰好呼应了前面提到过的选取编号最小的节点）
• 在\(x,y\)之间连接一条边。（注意前面的取出相当于删除）

最后，我们在点集中剩下的两个点中连一条边。

显然这有\(n-1\)条边，且绝对不会形成环，因此它是一棵树，且就是原树。

以上面的序列为例，我们可以模拟这一过程如下：

• 取出\(2,4\)连边。此时\(prufer\)序列：\(\{3,1,2,1\}\)，点集：\(\{1,2,3,5,6,7\}\)。
• 取出\(3,5\)连边。此时\(prufer\)序列：\(\{1,2,1\}\)，点集：\(\{1,2,3,6,7\}\)。
• 取出\(1,3\)连边。此时\(prufer\)序列：\(\{2,1\}\)，点集：\(\{1,2,6,7\}\)。
• 取出\(2,6\)连边。此时\(prufer\)序列：\(\{1\}\)，点集：\(\{1,2,7\}\)。
• 取出\(1,2\)连边。此时\(prufer\)序列：\(\{\}\)，点集：\(\{1,7\}\)。

最后再在\(1,7\)间连边，就可以得到原树了。

\(prufer\)序列的性质及相关结论

讲了这么多，我们最关键的还是\(prufer\)序列的一些性质，以及与其有关的一些结论。（毕竟前面也提到过，我也不知道这东西有什么实际意义）

• 重要性质：\(prufer\)序列与无根树一一对应。

  这应该显然吧，通过前面的介绍应该可以直接得出。

  而由这个性质，我们才能推导出后面的结论。

• 度数为\(d_i\)的节点会在\(prufer\)序列中出现\(d_i-1\)次。

  当某个节点度数为\(1\)时，会直接被删掉，否则每少掉一个相邻的节点，它就会在序列中出现\(1\)次。

  因此共出现\(d_i-1\)次。

• 一个\(n\)个节点的完全图的生成树个数为\(n^{n-2}\)。

  对于一个\(n\)个点的无根树，它的\(prufer\)序列长为\(n-2\)，而每个位置有\(n\)种可能性，因此可能的\(prufer\)序列有\(n^{n-2}\)种。

  又由于\(prufer\)序列与无根树一一对应，因此生成树个数应与\(prufer\)序列种树相同，即\(n^{n-2}\)。

• 对于给定度数为\(d_{1\sim n}\)的一棵无根树共有\(\frac{(n-2)!}{\prod_{i=1}^n(d_i-1)!}\)种情况。

  由上面的性质可以知道，度数为\(d_i\)的节点会在\(prufer\)序列中出现\(d_i-1\)次。

  则就是要求出\(d_i-1\)个\(i(1\le i\le n)\)的全排列个数。

  而上面那个式子就是可重全排列公式。（即全排列个数除以重复元素内部的全排列个数）

大致就是这些。

例题

下面有两道例题：【洛谷2290】[HNOI2004] 树的计数和【洛谷2624】[HNOI2008] 明明的烦恼。

实际上，这两道题都只用了由\(prufer\)序列所推导得到的结论，而没有真正构造\(prufer\)序列，应该也不算特别好的例题。。。