（第八场）G Counting regions 【欧拉公式】

题目链接：https://www.nowcoder.com/acm/contest/146/G

G、Counting regions

| 时间限制：1 秒 | 内存限制：128M
Niuniu likes mathematics. He also likes drawing pictures. One day, he was trying to draw a regular polygon with n vertices. He connected every pair of the vertices by a straight line as well. He counted the number of regions inside the polygon after he completed his picture. He was wondering how to calculate the number of regions without the picture. Can you calculate the number of regions modulo 1000000007? It is guaranteed that n is odd.

输入描述:

The only line contains one odd number n(3 ≤ n ≤ 1000000000), which is the number of vertices.

输出描述:

Print a single line with one number, which is the answer modulo 1000000007.

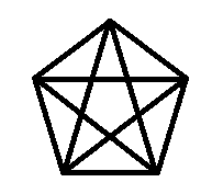
备注: The following picture shows the picture which is drawn by Niuniu when n=5. Note that no more than three diagonals share a point when n is odd.

示例 1

输入

3

输出

1

示例2

输入

5

输出

11

题意概括：

给你一个正n边形，将n个顶点两两连边，问内部有多少个区域。n是奇数。

官方题解：

欧拉公式：F=E-V+2
内部交点个数：C(n,4)
一条线段会被一个交点分成两段，所以x条直线的交点会多分出来x条线段，利用V 可以算出E。

解题思路：

根据欧拉公式：F：面数；E：边数；V：顶点数

当V >= 4时，多边形满足 V-E+F = 2；

因为N是奇数，所以任意选取四个顶点连接，两条对角线相交于一点，交点两两不重合，所以内部交点个数为 C(n, 4)；

而内部边数 = 对角线数 + 内部交点数*2 （即 C(n, 2) + C(n, 4)*2);

最后边数，结点数已知，可求面数。

注意细节：

求组合时数据偏大有取模操作，除法运算要通过逆元转换为乘法，这里求逆元的方法是用费马小定理。

AC code：

 ///欧拉公式+费马小定理求逆元
 #include <cstdio>
 #include <algorithm>
 #include <iostream>
 #include <cmath>
 #include <cstring>
 #define INF 0x3f3f3f3f
 #define ll long long int
 #define mod 1000000007
 using namespace std;

 ll N, V, E;
 ll quick_pow(ll a, ll b)
 {
     ll ans = ;
     while(b)
     {
         if(b&) ans = ans*a%mod;
         a = a*a%mod;
         b>>=;
     }
     return ans;
 }
 int main()
 {
     scanf("%lld", &N);
     V = N*(N-)%mod*(N-)%mod*(N-)%mod*quick_pow(,mod-)%mod;  ///内部交点
     E = (V* + (N*(N-)/)%mod)%mod;    ///边数
     V = (V + N)%mod;  ///顶点数
     ll F = ((E-V+)%mod+mod)%mod;  ///面数
     printf("%lld\n", F);
     return ;
 }