欧拉图 欧拉回路 欧拉通路 Euler的认识 （转）

转：https://www.cnblogs.com/Ash-ly/p/5397702.html

定义：

欧拉回路：图G的一个回路，如果恰通过图G的每一条边，则该回路称为欧拉回路，具有欧拉回路的图称为欧拉图。欧拉图就是从图上的一点出发，经过所有边且只能经过一次，最终回到起点的路径。

欧拉通路：即可以不回到起点，但是必须经过每一条边，且只能一次。也叫"一笔画"问题。

性质：

　　欧拉回路：一个欧拉回路，删掉一个点，仍然是一个欧拉回路。从一个欧拉回路拖走一个小欧拉回路，结果也是一个欧拉回路。

判定（充要）：

　　欧拉回路：1:  图G是连通的，不能有孤立点存在。

　　　　　　　2:  对于无向图来说度数为奇数的点个数为0;对于有向图来说每个点的入度必须等于出度。

　　欧拉通路：1:  图G是连通的，无孤立点存在。

　　　　　　　2:  对于无向图来说，度数为奇数的的点可以有2个或者0个，并且这两个奇点其中一个为起点另外一个为终点。对于有向图来说，可以存在两个点，其入度不等于出度，其中一个入度比出度大1，为路径的起点；另外一个出度比入度大1，为路径的终点。

算法（求欧拉回路）：

Fleury算法:

设图G是一个无向欧拉图，则按照下面算法求欧拉回路:

1:任取G中一个顶点v0,令P0 = v0.

2:假设沿Pi = v0e1v1e2v2……eivi 走到了顶点 vi,按照下面方法从E(i) = E(G) -  {e1, e2, e3,…,ei} 中选e(i ＋　1),选择后删除e(i +１)这条边.

　　a):e(i+1)余vi关联

　　b):除非无别的边可选，否则e(i+1)不应是Gi = G – {e1,e2,…,ei} 中的桥.假若迫不得已选的是桥,除删除这条边之外,还应该再把孤立点从Gi中移除(选择桥边必然会形成孤立的点).

3:当步骤 2 无法继续执行时停止算法.

当算法停止时，所得到的简单回路 Pm = = v0e1v1e2v2e3v3……emvm  (vm = v0) 为图G的一条欧拉回路.

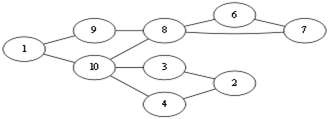
下面用图来描述：

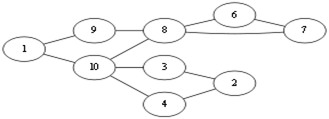
随便选择一个起点 v1。当前处在 v1 点，有两种走法 v1 – v9,v1 – v10，这俩条边都不是桥边，那么随便选择一个，<v1, v10>这条边吧。那么图就会成为这样.Eu = (走过的边集){<v1, v10>}

当前到了 V10 点，有<v10,v4>,<v10,v3>,<v10, v8>，先看<v10,v8>这条边吧，如果选择了这条边那么图就会成为这样：

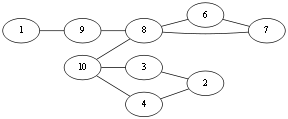
很显然形成了两个图，上下两个图不连通，即<v10, v8>这条边就是所谓的桥边，算法中说除非别无他选，否则不应该选择桥边，那么这条边就不能选择。回到上面，由于<v10,v4>,<v10,v3>都不是桥边，所以随便选择<v10,v4>吧. Eu={<v1, v10>,<v10,v4>}

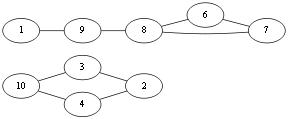
到了 v4 这个点，<v4, v2>这条边是桥边,但是别无选择，只好选择这条边.选择完这条边这时不仅要从原图中删除这条边，由于点4成为了孤点，所以这个点也该从原图删除。Eu={<v1,v10>,<v10,v4>,<v4,v2>}.

同理到达 v2 只好选择<v2,v3>，删除孤点 v2和边. Eu{<v1,v10>,<v10,v4>,<v4,v2><v2,v3>}.

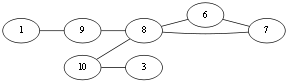
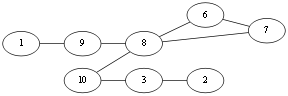
别无他选，<v3,v10>。Eu{<v1,v10>,<v10,v4>,<v4,v2><v2,v3><v3,v10>}.

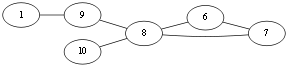
同样,选择<v10, v8>，Eu{<v1,v10>,<v10,v4>,<v4,v2><v2,v3><v3,v10>,<v10,v8>}.

此时到了 v8 同第一次到达v10时的情况，不能选择<v8,v9>这条桥边,选择<v8,v6>,Eu{<v1,v10>,<v10,v4>,<v4,v2><v2,v3><v3,v10>,<v10,v8>,<v8,v6>}.

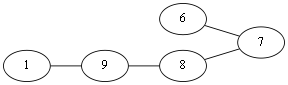
到达v6，选择<v6,v7>,删点删边,Eu{<v1,v10>,<v10,v4>,<v4,v2><v2,v3>,<v3,v10>,<v10,v8>,<v8,v6>,<v6,v7>}.以下就不给图了(逃;

然后接下来的选择都是别无他选,依次选择<v7,v8><v8,v9><v9,v1>，最后得到的欧拉边集Eu{<v1,v10>,<v10,v4>,<v4,v2><v2,v3>,<v3,v10>,<v10,v8>,<v8,v6>,<v6,v7>,<v7,v8><v8,v9><v9,v1>},于是我们就得到了一条欧拉回路.

代码：    

　　个人感觉时间复杂度不如基本法，主要是判断桥边的时间复杂度有点高，达到O(1)才和基本法一样，所以就放弃写了。

基本(套圈)法

　　首先从一个节点(v0)出发，随便往下走(走过的边需要标记一下，下次就别走了)，当走到不能再走的时候，所停止的点必然也是起点(因为所有的点的度数都是偶数，能进去肯定还会出来，再者中间有可能再次经过起点，但是如果起点还能继续走，那么就要继续往下搜索，直到再次回来时不能往下搜索为止)，然后停止时，走过的路径形成了一个圈，但因为是随便走的，所以可能有些边还没走就回来了，那些剩下的边肯定也会形成一个或者多个环，然后可以从刚才终止的节点往前回溯，找到第一个可以向其他方向搜索的节点(vi)，然后再以这个点继续往下搜索，同理还会继续回到该点(vi)，于是这个环加上上次那个环就构成了一个更大的环，即可以想象成形成了一条从 v0 到 vi的路径，再由 vi 走了一个环回到 vi，然后到达v0 的一条更长的路径，如果当前的路径还不是最长的，那么继续按照上面的方法扩展。只需要在回溯时记录下每次回溯的边，最后形成的边的序列就是一条欧拉回路。如果要记录点的顺序的话，那么每访问一个点，就把这个点压入栈中，当某个点不能继续搜索时，即在标记不能走的边是，这个点成为了某种意义上的孤点，然后把这个点输出最后得到的就是一条欧拉回路路径的点的轨迹。

　　总之，求欧拉回路的方法是，使用深度优先搜索，如果某条边被搜索到，则标记这条边为已选择，并且即使回溯也不能将当前边的状态改回未选择，每次回溯时，记录回溯路径。深度优先搜索结束后，记录的路径就是欧拉回路。

下面用图描述一遍：

假设我们选择从v1开始走,由于随便走，所以可能出现以下走法

第一步：v1 -- v9

第二步：v9 -- v8

第三步：v8 -- v10

第四步：v10 -- v1

此时由于走过的边不能再走，那么从 v1 就无法继续向下探索,所以往前回溯,记录边集Eu{<v1, v10>}，此时回溯到 v10 ,发现可以继续走，那么

第五步: v10 -- v3

第六步: v3 -- v2

第七步: v2 -- v4

第八步: v4 – v10

发现已经无路可走，那么继续回溯，记录回溯路径得到Eu{<v1,v10>, <v10, v4>, <v4, v2>, <v2, v3>, <v3, v10>, <v10, v8>}，此时回溯到了 v8.发现可以向其他方向搜索, 那么

第九步：v8 -- v6

第十步：v6 --v7

第十一步：v7-- v8

又无路可走，继续回溯Eu{<v1,v10>, <v10, v4>, <v4, v2>, <v2, v3>, <v3, v10>, <v10, v8>, <v8, v7>, <v7, v6>,<v6,v8>,<v8,v9>,<v9,v1>}，到这里整个DFS就结束了，我们得到的边集Eu就是一条欧拉回路。

具体实现与分析:

使用链式前向星和DFS实现寻找欧拉回路的算法，用链式前向星存无向边时每条边要存储两次。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
#include <queue>
using namespace std;

const int MAXV =  + ;
const int MAXE =  *  + ;
int head[MAXV];
int V, E;

typedef struct EdgeNode
{
    int to;
    int w;
    int next;
}edgeNode;
edgeNode Edges[MAXE];

bool visit[ * MAXE];
stack<int> stv;
queue<int> quv;//点集
queue<int> que;//边集

void EulerDFS(int now)
{
    st.push(now);//每访问一个点，就把该点压入栈
    for(int k = head[now]; k != -; k = Edges[k].next)
    {
        if(!visit[k])
        {
            visit[k] = true;            //有向图每条边保存了两次，也要标记两次
            if(k & )
                visit[k + ] = true;
            else
                visit[k - ] = true;
            EulerDFS(Edges[k].to);
            que.push(k);//回溯时记录边
        }
    }
    quv.push(stv.top());//记录点
    stv.pop();
}

int main()
{
    //freopen("in.txt", "r", stdin);
    scanf("%d%d", &V, &E);
    memset(head, -, sizeof(head));
    for(int i = ; i <= E; i++)
    {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        Edges[ * i - ].to = v;                //双向储存边
        Edges[ * i - ].w = w;
        Edges[ * i - ].next = head[u];
        head[u] =  * i - ;
        Edges[ * i].to = u;
        Edges[ * i].w = w;
        Edges[ * i].next = head[v];
        head[v] =  * i;
    }
    memset(visit, false, sizeof(visit));
    EulerDFS();
    return ;
}