hihoCoder#1121(二分图判定)

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

大家好，我是小Hi和小Ho的小伙伴Nettle，从这个星期开始由我来完成我们的Weekly。

新年回家，又到了一年一度大龄剩男剩女的相亲时间。Nettle去姑姑家玩的时候看到了一张姑姑写的相亲情况表，上面都是姑姑介绍相亲的剩男剩女们。每行有2个名字，表示这两个人有一场相亲。由于姑姑年龄比较大了记性不是太好，加上相亲的人很多，所以姑姑一时也想不起来其中有些人的性别。因此她拜托我检查一下相亲表里面有没有错误的记录，即是否把两个同性安排了相亲。

OK，让我们愉快的暴力搜索吧！

才怪咧。

对于拿到的相亲情况表，我们不妨将其转化成一个图。将每一个人作为一个点(编号1..N)，若两个人之间有一场相亲，则在对应的点之间连接一条无向边。(如下图)

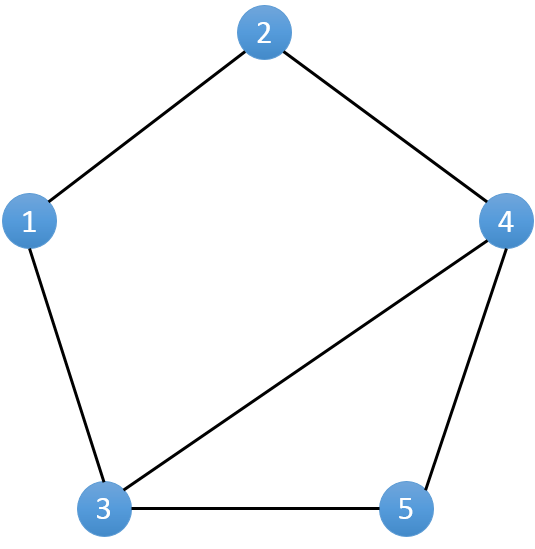
因为相亲总是在男女之间进行的，所以每一条边的两边对应的人总是不同性别。假设表示男性的节点染成白色，女性的节点染色黑色。对于得到的无向图来说，即每一条边的两端一定是一白一黑。如果存在一条边两端同为白色或者黑色，则表示这一条边所表示的记录有误。

由于我们并不知道每个人的性别，我们的问题就转化为判定是否存在一个合理的染色方案，使得我们所建立的无向图满足每一条边两端的顶点颜色都不相同。

那么，我们不妨将所有的点初始为未染色的状态。随机选择一个点，将其染成白色。再以它为起点，将所有相邻的点染成黑色。再以这些黑色的点为起点，将所有与其相邻未染色的点染成白色。不断重复直到整个图都染色完成。(如下图)

在染色的过程中，我们应该怎样发现错误的记录呢？相信你一定发现了吧。对于一个已经染色的点，如果存在一个与它相邻的已染色点和它的颜色相同，那么就一定存在一条错误的记录。(如上图的4，5节点)

到此我们就得到了整个图的算法：

1. 选取一个未染色的点u进行染色
2. 遍历u的相邻节点v：若v未染色，则染色成与u不同的颜色，并对v重复第2步；若v已经染色，如果 u和v颜色相同，判定不可行退出遍历。
3. 若所有节点均已染色，则判定可行。

接下来就动手写写吧！

输入

第1行：1个正整数T(1≤T≤10)

接下来T组数据，每组数据按照以下格式给出：

第1行：2个正整数N,M(1≤N≤10,000，1≤M≤40,000)

第2..M+1行：每行两个整数u,v表示u和v之间有一条边

输出

第1..T行：第i行表示第i组数据是否有误。如果是正确的数据输出”Correct”，否则输出”Wrong”

样例输入

2
5 5
1 2
1 3
3 4
5 2
1 5
5 5
1 2
1 3
3 4
5 2
3 5

样例输出

Wrong
Correct
注意:存在多个连通分量。

#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
const int MAXN=;
int n,m;
vector<int> arc[MAXN];
int color[MAXN];
bool bfs(int src)
{
    queue<int> que;
    que.push(src);
    color[src]=;
    while(!que.empty())
    {
        int u=que.front();que.pop();
        for(int i=;i<arc[u].size();i++)
        {
            int to=arc[u][i];
            if(color[to]==-)
            {
                que.push(to);
                color[to]=(color[u]==)?:;
            }
            else if(color[to]==color[u])    return false;
        }
    }
    return true;
}
bool solve()// 存在多个连通分量
{
    for(int i=;i<=n;i++)
    {
        if(color[i]==-)
        {
            if(!bfs(i))    return false;
        }
    }
    return true;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&m);
        memset(color,-,sizeof(color));
        for(int i=;i<=n;i++)    arc[i].clear();
        for(int i=;i<m;i++)
        {
            int u,v;
            scanf("%d%d",&u,&v);
            arc[u].push_back(v);
            arc[v].push_back(u);
        }
        if(solve())
        {
            printf("Correct\n");
        }
        else
        {
            printf("Wrong\n");
        }
    }
    return ;
}