[洛谷P1390]公约数的和·莫比乌斯反演

公约数的和

传送门

---

放在这么前面的位置当然是给自己看的！！！！！

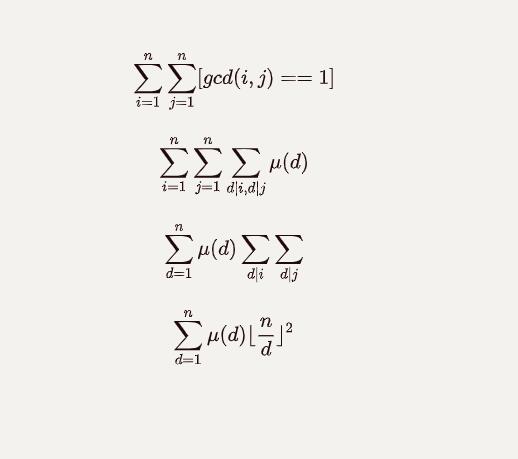
这一步原来是这么推过来的！如果下次再忘了怎么推可以这么搞出来或者直接记结论

---

分析

这道题很显然答案为

\[Ans=\sum_{i=1}^n\sum_{j=i+1}^n (i,j)
\]

//其中\((i,j)\)意味\(gcd(i,j)\)

这样做起来很烦，看起来是\(O(N^2)\)的辣鸡复杂度，我们考虑这个问题的弱化版

求$$\sum_{i=1}^n\sum_{j=1}n(i,j)$$

然后通过一些优美的容斥就可以算出原答案

现在我们设$$f(d)=\sum_{i=1}^n\sum_{j=1}n[(i,j)=d]$$

这个式子表示，在\(i=1..n，j=1..n，gcd(i,j)=d\)的个数，其中\([]\)内成立，返回值为\(1\)，否则为\(0\)

我们令

\[F(n)=\sum_{n|d}f(d)=\lfloor\frac N n\rfloor^2
\]

则有

\[f(n)=\sum_{n|d}\mu(\frac d n)F(d)$$$$=\sum_{n|d}\mu(\frac d n)\lfloor\frac N d\rfloor^2
\]

考虑\(Ans\)

\[Ans=\sum_{i=1}^n\sum_{j=1}^n(i,j)
\]

\[=\sum_{d=1}^n d\sum_{i=1}^n\sum_{j=1}^n[(i,j)=d]
\]

\[=\sum_{d=1}^n d\;f(d)
\]

考虑把\(f(d)\)的式子带入，这时我们不枚举\(d\)的倍数具体是多少，而是枚举倍数（不枚举\(d|n\)的\(n\),而是枚举\(\frac n d\)，比如说我们用\(k\)表示,就有

\[=\sum_{d=1}^N d \sum_{k=1}^N\mu(k)\lfloor\frac{N}{dk}\rfloor^2
\]

这个\(dk\)感觉不是很舒服，我们令\(t=dk，将枚举d改为枚举dk，则有\)

\[=\sum_{t=1}^N\sum_{k|t} k\mu(\frac{t}{k})\lfloor\frac{N}{t}\rfloor^2
\]

观察$$\sum_{k|t} k\mu(\frac{t}{k})$$

我们发现这是在前文提及的狄利克雷卷积

\[\mu\times d=\phi
\]

（忘了的话戳这里）

本篇·莫比乌斯反演

那么原式就优美的化简为

\[\sum_{t=1}^N\phi(t)\lfloor\frac{N}{t}\rfloor^2
\]

这样一个式子已经可以\(O(N)\)地解决了，更优美地也可以进行整除分块，做到计算\(\sqrt{n}\)

关于最前面的容斥，只需要减去\(gcd(i,i)=i\)和\(gcd(i,j)=gcd(j,i)\)的情况就可以

对于\(gcd(i,i)=i\)的情况，考虑在\(\sum_{i=1}^n\sum_{j=1}^n(i,j)\)中，对于每个\(i\)，有且仅有\(1\)个\(j=i\)对应，此时的贡献为\(i\)，所以总贡献为

\(\sum_{i=1}^N i=N(N+1)/2\)

而\(gcd(i,j)=gcd(j,i)\)的情况，去掉情况\(1\)后显然这两个对半分，只要\(/2\)即可

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=2000010;
LL sum[maxn];
int vis[maxn],phi[maxn],pri[maxn];
int cnt=0,n;
inline void getphi(int n){
    memset(vis,0,sizeof(vis));phi[1]=vis[1]=1;
    for (int i=2;i<=n;i++){
        if (!vis[i]){pri[++cnt]=i;phi[i]=i-1;}
        for (int j=1;j<=cnt&&(LL)i*pri[j]<=n;j++){
            vis[i*pri[j]]=1;
            if (i%pri[j]==0){phi[i*pri[j]]=phi[i]*pri[j];break;}
            else phi[i*pri[j]]=phi[i]*(pri[j]-1);
        }
    }
    for (int i=1;i<=n;i++) sum[i]=sum[i-1]+phi[i];
}
int main(){
    scanf("%d",&n);
    getphi(n);
    LL ans=0;
    for (int l=1,r;l<=n;l=r+1){
        r=n/(n/l);
        ans+=(LL)(sum[r]-sum[l-1])*(n/l)*(n/l);
    }
    printf("%lld",(ans-(LL)n*(n+1)/2)/2);
    return 0;
}