BZOJ 5421: 收藏家

传送门

直接搞很复杂，考虑转化问题

题目只要求第1个人最多能获得的物品数量

所以如果一种物品拥有多个和一个是没区别的

那么考虑每种物品对第1个人怎样贡献

显然要经过一些交换最终到达第一个人那里

发现很像一个流，那么考虑建立网络流模型

建一个源点向每个点连一条最大流量为1的边，相当于初始每个点有1个物品

点1向汇点连一条 $a_1$ 的边，因为点1最多能放 $a_1$ 个物品

因为一个点 i 同时最多只能有 $a_i$ 种物品，所以也把其他个点拆成两个，之间连一条流量为 $a_i$ 的边

考虑点与点之间的连接

因为交换是按时间顺序的，所以不可能直接连

同样拆点

把一个点 i 分成 m 个点，表示 i 在 1~m 的时间点上的状态，显然这 m 个点之间的流量为 $a_i$（一个点 i 最多同时有 $a_i$ 种不同的物品）

这样就可以把不同的点连起来了

具体说来就是：如果在时间 i ， a 和 b 发生了交换，那么在 a 拆出来的第 i 个点和 b 拆出来的第 i 个点之间连双向边

显然边权均为 1 （一次只能换一个物品）

可以参照下面的丑图：

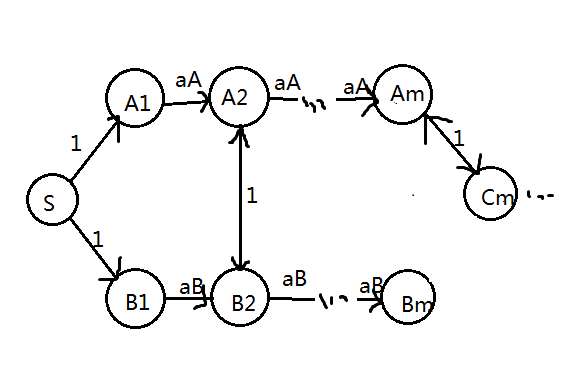
但是这样有$nm$个点，显然不行

但是可以发现只有向其他点连接的点是有用的，即一串 m 个点只有向外面其他点有连接的点是有用的，所以我们动态地加点连边，只有对于需要的点我们才要连边

这样因为边数是 m 所以要加的点数就是 2m

要注意一些细节

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
using namespace std;
typedef long long ll;
inline int read()
{
    int x=,f=; char ch=getchar();
    while(ch<''||ch>'') {if(ch=='-') f=-; ch=getchar(); }
    while(ch>=''&&ch<='') { x=(x<<)+(x<<)+(ch^); ch=getchar(); }
    return x*f;
}
const int N=3e5+,INF=1e9+;
int fir[N],from[N<<],to[N<<],val[N<<],cntt=,Fir[N];
inline void add(int a,int b,int c)
{
    from[++cntt]=fir[a]; fir[a]=cntt;
    to[cntt]=b; val[cntt]=c;
    from[++cntt]=fir[b]; fir[b]=cntt;
    to[cntt]=a; val[cntt]=;
}
queue <int> q;
int n,m,tot,ans;
int S,T,p[N],pre[N],dep[N];
//p是每个点的容量,pre[i]是为了动态加点，存点i的上个时间的点的编号
//以下为Dinic
bool BFS()
{
    memset(dep,,sizeof(dep));
    q.push(S); dep[S]=; int x;
    while(!q.empty())
    {
        x=q.front(); q.pop();
        for(int i=fir[x];i;i=from[i])
        {
            int &v=to[i]; if(dep[v]||!val[i]) continue;
            dep[v]=dep[x]+; q.push(v);
        }
    }
    for(int i=;i<=tot;i++) Fir[i]=fir[i];
    return dep[T] ?  : ;
}
int DFS(int x,int mif)
{
    if(!mif||x==T) return mif;
    int fl=,res=;
    for(int i=Fir[x];i;i=from[i])
    {
        Fir[x]=i; int &v=to[i]; if(dep[v]!=dep[x]+) continue;
        if( res=DFS(v, min(mif,val[i]) ) )
        {
            fl+=res; mif-=res;
            val[i]-=res; val[i^]+=res;
            if(!mif) break;
        }
    }
    return fl;
}
//以上为Dinic
void slove()//处理读入
{
    int a,b; ans=tot=; cntt=;//多组数据记得初始化
    memset(fir,,sizeof(fir));
    n=read(); m=read();
    S=++tot; T=++tot;//建源点和汇点
    for(int i=;i<=n;i++)
    {
        add(S,pre[i]=++tot,);//源点向每个初始点连边
        p[i]=read();
    }
    while(m--)
    {
        a=read(); b=read();
        int na=++tot,nb=++tot;//新的时间的点
        add(pre[a],na,p[a]); add(pre[b],nb,p[b]);//和上一时间的点相连
        add(na,nb,); add(nb,na,);//之间连双向边
        pre[a]=na; pre[b]=nb;//更新pre
    }
    add(pre[],T,p[]);//最后点1连向汇点，容量为p[1]
    while(BFS()) ans+=DFS(S,INF);
    printf("%d\n",ans);
}
int main()
{
    //freopen("collection.in","r",stdin);
    //freopen("collection.out","w",stdout);
    int T=read();
    while(T--) slove();
    return ;
}