nyoj299——如何优雅的写矩阵快速幂

Matrix Power Series

时间限制：1000 ms  |  内存限制：65535 KB

难度：4

 

描述

Given a n × n matrix A and a positive integer k, find the sum S = A + A² + A³ + … + A^k.

 

输入

The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 10^9) and m (m < 10^4). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.

输出

Output the elements of S modulo m in the same way as A is given.

样例输入

2 2 4
0 1
1 1

样例输出

1 2
2 3

#include<bits/stdc++.h>
using namespace std;
typedef long long  ll;
const int maxn = ;
const int moder = ;

const int N=;
int c[N][N],a[N][N],b[N][N],n,mo;
void mult(int x[N][N],int y[N][N])//x = x*y
{
    int i,j,k;
    for (i=;i<=n;i++)
        for (j=;j<=n;j++)
        {
            c[i][j]=;
            for (k=;k<=n;k++) c[i][j]=(c[i][j]+x[i][k]*y[k][j])%mo;
        }
    for (i=;i<=n;i++)
        for (j=;j<=n;j++) x[i][j]=c[i][j];
}

int main()
{
    int m,i,j;
    scanf("%d%d%d",&n,&m,&mo);
    for (i=;i<=n;i++)
    {
        for (j=;j<=n;j++) scanf("%d",&a[i][j]);
        a[i][i+n]=a[i+n][i+n]=b[i][i]=b[i+n][i+n]=; //b单位矩阵，a为所求的基础矩阵
    }
    n*=;
    m++;
    while(m>)
    {
        if (m%) mult(b,a);
        m/=;
        mult(a,a);
    }
    n/=;
    for (i=;i<=n;i++) b[i][i+n]--;
    for (i=;i<=n;i++)
    {
        for (j=;j<n;j++) printf("%d ",b[i][j+n]);
        printf("%d\n",b[i][j+n]);
    }
    return ;
}

网上看了许多快速幂的写法，感觉都很麻烦，只有这个写的很通俗易懂

但题目要求的是 A+A²+...+A^k，而不是单个矩阵的幂

　　那么我们可以构造一个分块的辅助矩阵 S，其中 A 为原矩阵，E 为单位矩阵，O 为0矩阵

　　

　　我们将 S 取幂，会发现一个特性

　　

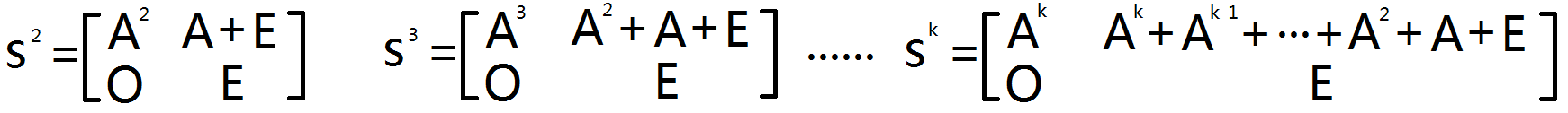
　　S^k 右上角那一块不正是我们要求的 A+A²+...+A^k 吗？

　　于是我们构造出 S 矩阵，然后对它求矩阵快速幂即可，最后别忘了减去一个单位阵

转自 https://www.cnblogs.com/hadilo/p/5903514.html