4. Median of Two Sorted Arrays(2个有序数组的中位数)

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

Example 1:

nums1 = [1, 3]
nums2 = [2]
 
The median is 2.0

Example 2:

nums1 = [1, 2]
nums2 = [3, 4]
 
The median is (2 + 3)/2 = 2.5
 

假设我们要找第 7 小的数字。

我们比较两个数组的第 k / 2 个数字，如果 k 是奇数，向下取整。也就是比较第 3 个数字，上边数组中的 4 和 下边数组中的 3 ，如果哪个小，就表明该数组的前 k / 2 个数字都不是第 k 小数字，所以可以排除。也就是 1，2，3 这三个数字不可能是第 7 小的数字，我们可以把它排除掉。将 1349 和 45678910 两个数组作为新的数组进行比较。

更一般的情况 A [ 1 ]，A [ 2 ]，A [ 3 ]，A [ k / 2] ... ，B[ 1 ]，B [ 2 ]，B [ 3 ]，B[ k / 2] ... ，如果 A [ k / 2 ] < B [ k / 2 ] ，那么 A [ 1 ]，A [ 2 ]，A [ 3 ]，A [ k / 2] 都不可能是第 k 小的数字。

A 数组中比 A [ k / 2 ] 小的数有 k / 2 - 1 个，B 数组中，B [ k / 2 ] 比 A [ k / 2 ] 小，假设 B [ k / 2 ] 前边的数字都比 A [ k / 2 ] 小，也只有 k / 2 - 1 个，所以比 A [ k / 2 ] 小的数字最多有 k / 2 - 1 + k / 2 - 1 = k - 2 个，所以 A [ k / 2 ] 最多是第 k - 1 小的数。而比 A [ k / 2 ] 小的数更不可能是第 k 小的数了，所以可以把它们排除。

橙色的部分表示已经去掉的数字。

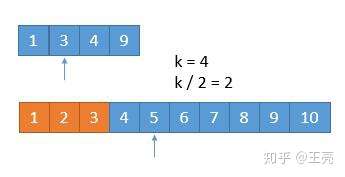
由于我们已经排除掉了 3 个数字，就是这 3 个数字一定在最前边，所以在两个新数组中，我们只需要找第 7 - 3 = 4 小的数字就可以了，也就是 k = 4 。此时两个数组，比较第 2 个数字，3 < 5，所以我们可以把小的那个数组中的 1 ，3 排除掉了。

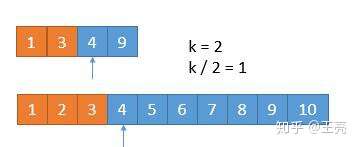
我们又排除掉 2 个数字，所以现在找第 4 - 2 = 2 小的数字就可以了。此时比较两个数组中的第 k / 2 = 1 个数，4 == 4 ，怎么办呢？由于两个数相等，所以我们无论去掉哪个数组中的都行，因为去掉 1 个总会保留 1 个的，所以没有影响。为了统一，我们就假设 4 > 4 吧，所以此时将下边的 4 去掉。

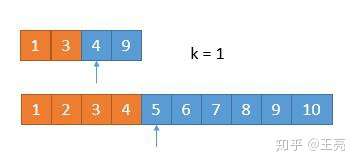
由于又去掉 1 个数字，此时我们要找第 1 小的数字，所以只需判断两个数组中第一个数字哪个小就可以了，也就是 4 。

所以第 7 小的数字是 4 。

我们每次都是取 k / 2 的数进行比较，有时候可能会遇到数组长度小于 k / 2 的时候。

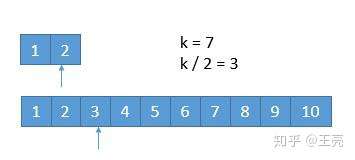
此时 k / 2 等于 3 ，而上边的数组长度是 2 ，我们此时将箭头指向它的末尾就可以了。这样的话，由于 2 < 3 ，所以就会导致上边的数组 1，2 都被排除。造成下边的情况。

由于 2 个元素被排除，所以此时 k = 5 ，又由于上边的数组已经空了，我们只需要返回下边的数组的第 5 个数字就可以了。

从上边可以看到，无论是找第奇数个还是第偶数个数字，对我们的算法并没有影响，而且在算法进行中，k 的值都有可能从奇数变为偶数，最终都会变为 1 或者由于一个数组空了，直接返回结果。

所以我们采用递归的思路，为了防止数组长度小于 k / 2 ，所以每次比较 min ( k / 2，len ( 数组 ) ) 对应的数字，把小的那个对应的数组的数字排除，将两个新数组进入递归，并且 k 要减去排除的数字的个数。递归出口就是当 k = 1 或者其中一个数字长度是 0 了。

对于一个长度为n的已排序数列a，若n为奇数，中位数为a[n / 2 + 1] ,
    若n为偶数，则中位数(a[n / 2] + a[n / 2 + 1]) / 2
    如果我们可以在两个数列中求出第K小的元素，便可以解决该问题
    不妨设数列A元素个数为n，数列B元素个数为m，各自升序排序，求第k小元素(k=m+n)
    取A[k / 2] B[k / 2] 比较，
    如果 A[k / 2] > B[k / 2] 那么，所求的元素必然不在B的前k / 2个元素中(证明反证法)
    反之，必然不在A的前k / 2个元素中，于是我们可以将A或B数列的前k / 2元素删去，求剩下两个数列的
    k - k / 2小元素，于是得到了数据规模变小的同类问题，递归解决
    如果 k / 2 大于某数列个数，所求元素必然不在另一数列的前k / 2个元素中，同上操作就好。
 

需要尝试对两个数组同时进行二分查找，逐步排除掉不可能出现中位数的区间，最后找到所求的中位数。这种解法的主要思想就是： 
如果数组a的中位数小于数组b的中位数，那么整体的中位数只可能出现在a的右区间加上b的左区间之中； 
如果数组a的中位数大于等于数组b的中位数，那么整体的中位数只可能出现在a的左区间加上b的右区间之中。 
关键就是利用分治的思想逐渐缩小a的区间和b的区间来找到中位数。

 class Solution {
     public double findMedianSortedArrays(int[] nums1, int[] nums2) {
         double res = 0.0;
         int n = nums1.length;
         int m = nums2.length;
         if((m+n)%2==1)
             res = (double)kth(nums1,nums2,0,0,(m+n+1)/2);
         else
             res = (double) ( kth(nums1,nums2,0,0,(m+n)/2) +
                             kth(nums1,nums2,0,0,(m+n)/2+1))/2;
         return res;
 
     }
     private int kth(int[] a,int[] b,int alo,int blo,int k){
         if(alo>=a.length) return b[blo+k-1];
         if(blo>=b.length) return a[alo+k-1];
         if(k==1) return Math.min(a[alo],b[blo]);
 
         int aMid = Integer.MAX_VALUE, bMid = Integer.MAX_VALUE;
 
         if(alo+k/2-1<a.length)
             aMid = a[alo+k/2-1];
         if(blo+k/2-1<b.length)
             bMid = b[blo+k/2-1];
 
         if(aMid>bMid)
             return kth(a,b,alo,blo+k/2,k-k/2);
         else
             return kth(a,b,alo+k/2,blo,k-k/2);
     }
 }