BZOJ1407 NOI2002 Savage 【Exgcd】

BZOJ1407 NOI2002 Savage

---

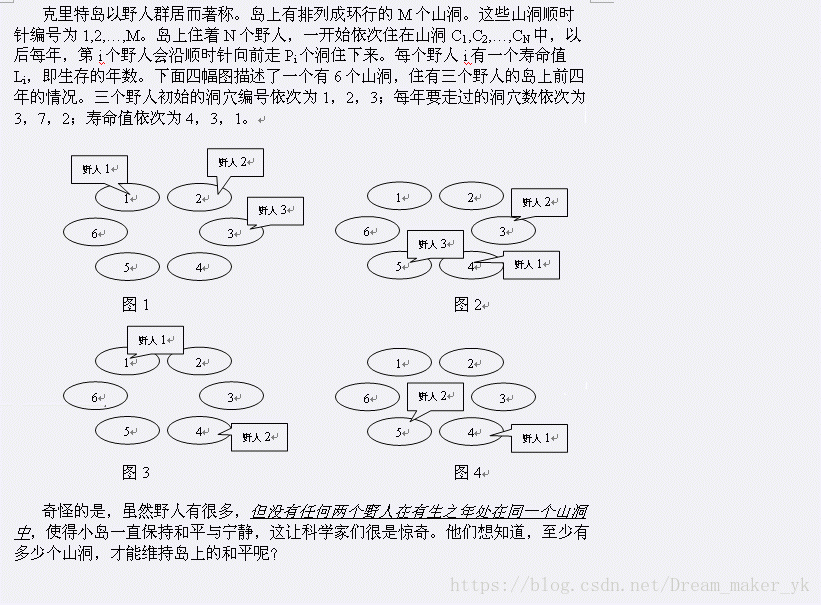
Description

Input

第1行为一个整数N(1<=N<=15)，即野人的数目。

第2行到第N+1每行为三个整数Ci, Pi, Li表示每个野人所住的初始洞穴编号，每年走过的洞穴数及寿命值。

(1<=Ci,Pi<=100, 0<=Li<=10^6 )

Output

仅包含一个数M，即最少可能的山洞数。输入数据保证有解，且M不大于10^6。

Sample Input

3

1 3 4

2 7 3

3 2 1

Sample Output

6

//该样例对应于题目描述中的例子。

---

首先看到了M<=1e6，然后就可以暴力枚举M的值

然后确定了M的值之后，我们对于两个野人i和j可以列出

(Ci+x∗pi)−(Cj+x∗pj)=y∗M" role="presentation">(Ci+x∗pi)−(Cj+x∗pj)=y∗M(Ci+x∗pi)−(Cj+x∗pj)=y∗M

当x≤min(li,lj)" role="presentation">x≤min(li,lj)x≤min(li,lj)的时候就不成立(会相遇)

求出x的最小整数解判断一下就行了

---

#include<bits/stdc++.h>
using namespace std;
#define N 20
#define M 1000000
int n;
int c[N],p[N],l[N];
void exgcd(int a,int b,int &x,int &y){
    if(!b)x=1,y=0;
    else{
        exgcd(b,a%b,y,x);
        y-=(a/b)*x;
    }
}
int gcd(int a,int b){
    if(!b)return a;
    return gcd(b,a%b);
}
bool judge(int i,int j,int s){
    int anow=p[i]-p[j],bnow=s,cnow=c[j]-c[i];
    int x,y,d=gcd(anow,bnow);
    if(cnow%d)return 1;
    exgcd(anow,bnow,x,y);
    int w=abs(s/d);
    x=((x*cnow/d)%w+w)%w;
    if(x<=l[i]&&x<=l[j])return 0;
    return 1;
}
bool check(int s){
    for(int i=1;i<=n;i++)
        for(int j=i+1;j<=n;j++)
            if(!judge(i,j,s))return 0;
    return 1;
}
int main(){
    int down=0;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d%d%d",&c[i],&p[i],&l[i]),down=max(down,c[i]);
    for(int i=down;i<=M;i++)
        if(check(i)){printf("%d",i);return 0;}
    return 0;
}