基于python的数学建模---pulp库

instance

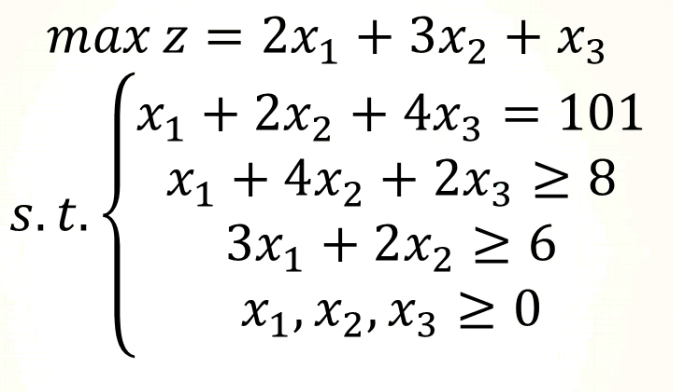
代码：

import pulp

z = [2, 3, 1]
a = [[1, 4, 2], [3, 2, 0]]
b = [8, 6]
aeq = [[1,2,4]]
beq = [101]
#确定最大化最小化问题，最大化只需将Min改成Max即可
m = pulp.LpProblem(sense=pulp.LpMinimize)
# 定义三个变量放到列表中
x = [pulp.LpVariable(f'x{i}', lowBound=0) for i in [1, 2, 3]]
#定义目标函数，lopDot可以将两个列表的对应位相乘再相加
#相当于z[0]*x[0]+....
m += pulp.lpDot(z,x)
#设置不等式约束条件
for i in range(len(a)):
    m += pulp.lpDot(a[i], x) >= b[i]
#设置等式约束条件
for i in range(len(aeq)):
    m += pulp.lpDot(aeq[i],x) == beq[i]
#求解
m.solve()
#输出结果
print(f'优化结果：{pulp.value(m.objective)}')
print(f'参数取值：{[pulp.value(var) for var in x]}')

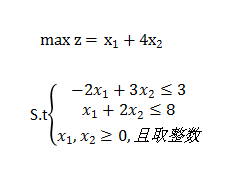
import numpy as np
import pulp as pl

def main():
    ProbLp=pl.LpProblem("ProbLp",sense=pl.LpMaximize)
    print(ProbLp.name)
    x1=pl.LpVariable('x1',lowBound=0,upBound=None,cat='Integer')
    x2=pl.LpVariable('x2',lowBound=0,upBound=2,cat='integer')

    ProbLp+=(x1+4*x2)
    ProbLp+=(-2*x1+3*x2<=3)
    ProbLp+=(x1+2*x2<=8)
    ProbLp.solve()
    print("Shan Status:", pl.LpStatus[ProbLp.status])  # 输出求解状态
    for v in ProbLp.variables():
        print(v.name, "=", v.varValue)  # 输出每个变量的最优值
    print("F(x) =", pl.value(ProbLp.objective))  # 输出最优解的目标函数值

if __name__ =='__main__':
    main()

ProbLp
Shan Status: Optimal
x1 = 4.0
x2 = 2.0
F(x) = 12.0