图解B树及C#实现（2）数据的读取及遍历

目录

• 前言
• 查询数据
  • 算法说明
  • 代码实现
• 查询最值
  • 算法说明
  • 代码实现
• B树的遍历
  • 算法说明
  • 代码实现
• Benchmarks
• 总结
• 参考资料

前言

本文为系列文章

1. B树的定义及数据的插入
2. 数据的读取及遍历（本文）
3. 数据的删除

前一篇文章为大家介绍了 B树 的基本概念及其插入算法。本文将基于前一篇的内容，为大家介绍插入到 B树 中的数据该怎么读取及遍历，

本文的代码基于前一篇文章的代码，已经实现的功能可能会被省略，只介绍新增的功能。

在本文开始前，再次复习下 B树 的顺序特性：

• 每个 节点 中的 Item 按 Key 有序排列（规则可以是自定义的）。
• 升序排序时，每个 Item 左子树 中的 Item 的 Key 均小于当前 Item 的 Key。
• 升序排序时，每个 Item 右子树 中的 Item 的 Key 均大于当前 Item 的 Key。

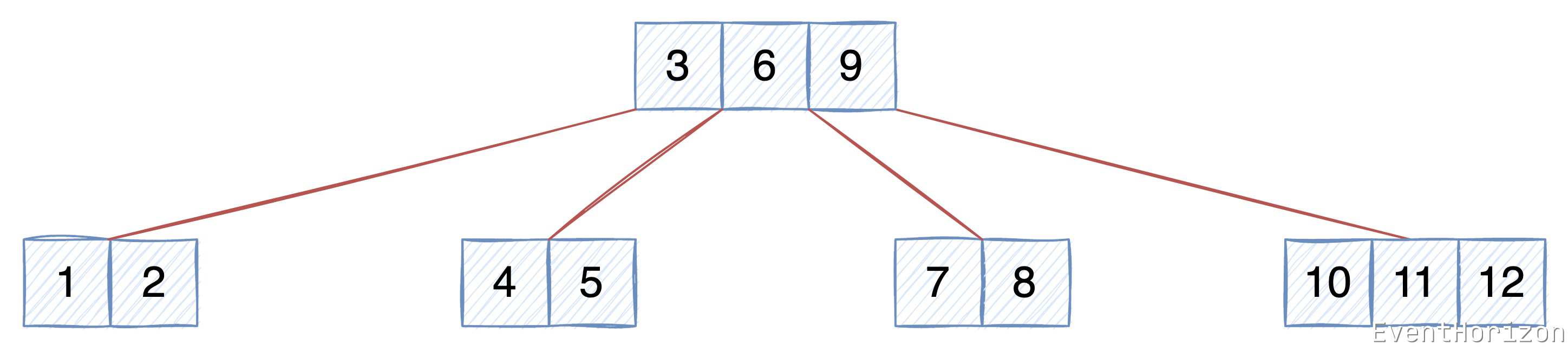
理解数据的顺序性对本文的理解至关重要。

查询数据

算法说明

B树 是基于二分查找算法进行设计的，某些资料中你也会看到用 多路搜索树 来归类 B树。

在 B树 中查找数据时，二分体现在两个方面：

1. 在节点中查找数据时，使用二分查找算法。
2. 当节点中找不到数据时，使用二分查找算法找到下一个节点。

具体的查找过程如下：

1. 从根节点开始，在节点中使用二分查找算法查找数据。
2. 如果没有找到数据，则根据查找的 Key 值与节点中的 Key 值的大小关系，决定下一个节点的位置。
3. 重复步骤 1 和 2，直到找到数据或者找到叶子节点。如果在叶子节点中也没有找到数据，则说明数据不存在。

举例说明：

在下面的 B树 中，查找 Key 为 8 的数据。

1. 从根节点开始，使用二分查找算法没有找到数据
2. 根据 Key 值与节点中的 Key 值的大小关系，决定下一个节点的位置应该在 6 和 9 之间，也就是 6 的右子树。
3. 在 6 的右子树中，使用二分查找算法找到了数据。
   
   

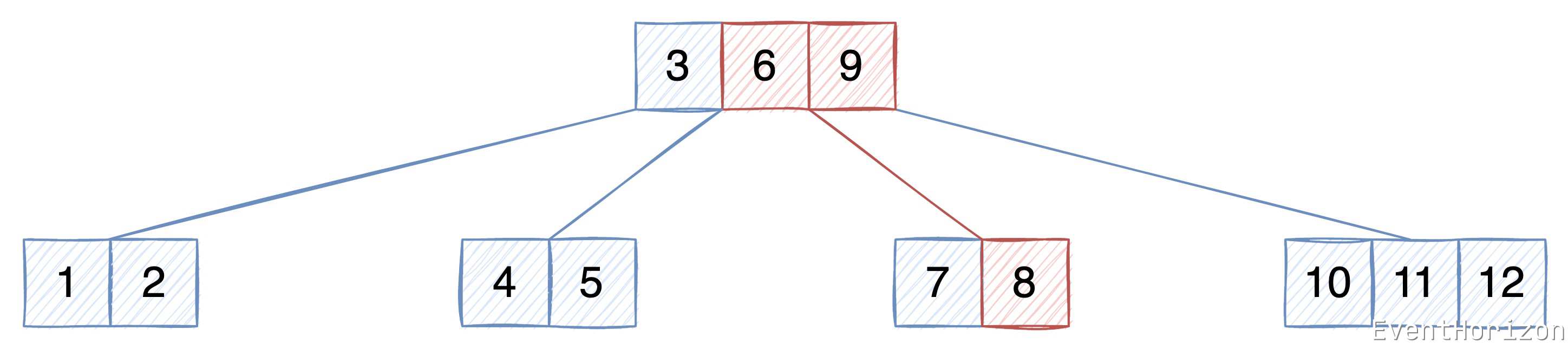
代码实现

前一篇文章我们定义了 Items 类，用于存储节点中的数据，并且在一开始就定义了一个二分查找算法，用于在 Items 查找 Item。

前一篇用它来找到合适的插入位置，现在我们用寻找已经存在的数据。

在当前节点找到 Item 时，index 对应的就是 Item 的位置。没找到时则代表下一个子树的索引。

理解代码时请参考下图：

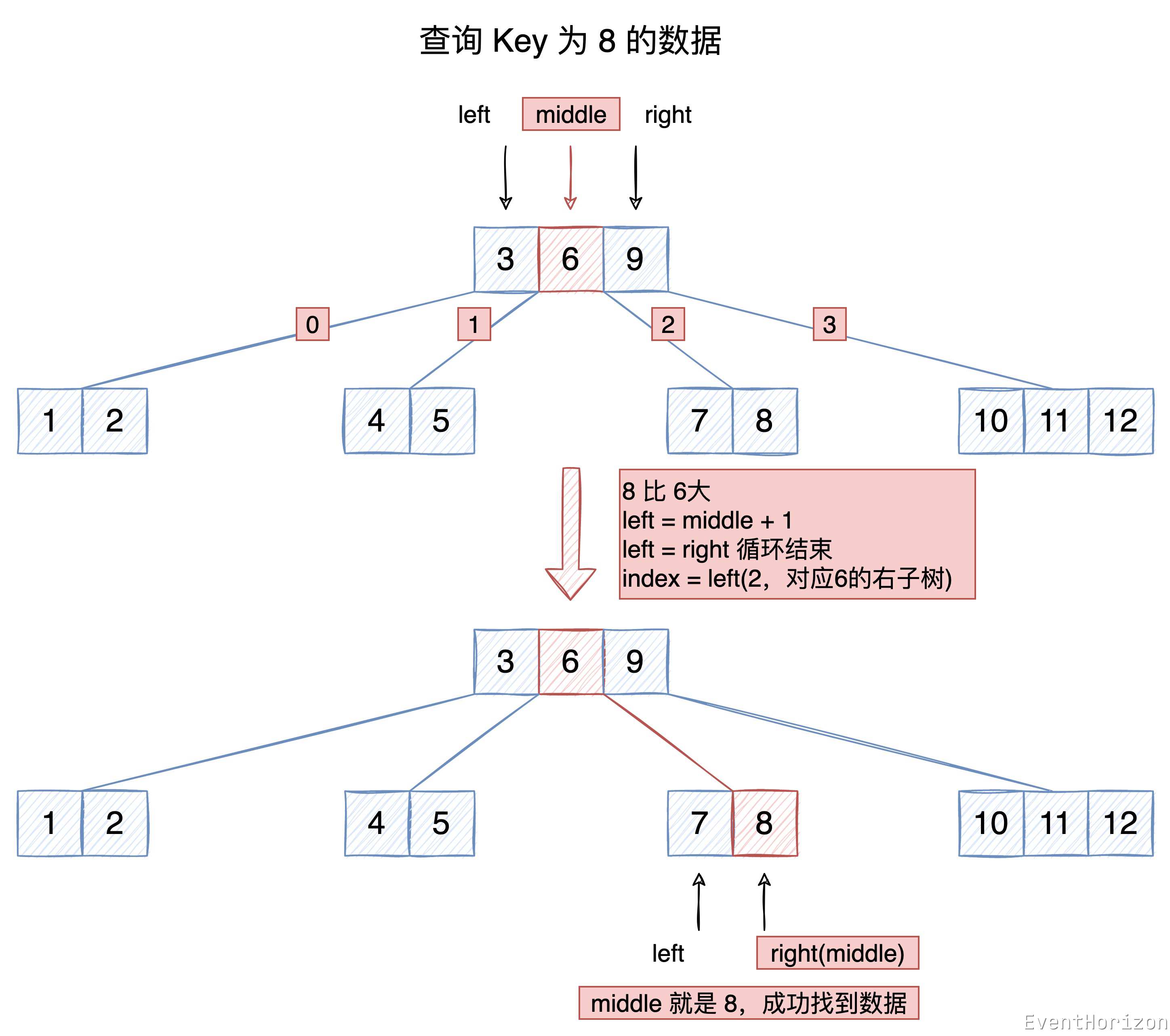
internal class Items<TKey, TValue>
{
    public bool TryFindKey(TKey key, out int index)
    {
        if (_count == 0)
        {
            index = 0;
            return false;
        }

        // 二分查找
        int left = 0;
        int right = _count - 1;
        while (left <= right)
        {
            int middle = (left + right) / 2;
            var compareResult = _comparer.Compare(key, _items[middle]!.Key);
            if (compareResult == 0)
            {
                index = middle;
                return true;
            }

            if (compareResult < 0)
            {
                right = middle - 1;
            }
            else
            {
                left = middle + 1;
            }
        }

        index = left;
        return false;
    }
}

在 Node 中，我们需要找到合适的子树，然后递归调用子节点的 TryFind 方法。

internal class Node<TKey, TValue>
{
    public bool TryFind(TKey key, out Item<TKey, TValue?> item)
    {
        if (_items.TryFindKey(key, out int index))
        {
            item = _items[index];
            return true;
        }

        if (IsLeaf)
        {
            item = default!;
            return false;
        }

        return _children[index].TryFind(key, out item);
    }
}

BTree 类中，我们只需要调用根节点的 TryFind 方法即可。

public sealed class BTree<TKey, TValue> : IEnumerable<KeyValuePair<TKey, TValue?>>
{
    public bool TryGetValue([NotNull] TKey key, out TValue? value)
    {
        ArgumentNullException.ThrowIfNull(key);

        if (_root == null)
        {
            value = default;
            return false;
        }

        if (!_root.TryFind(key, out var item))
        {
            value = default;
            return false;
        }

        value = item.Value;
        return true;
    }
}

查询最值

算法说明

B树的顺序性使得我们可以很方便的找到最值。

1. 最小值：从根节点开始，一直往左子树走，直到叶子节点。
2. 最大值：从根节点开始，一直往右子树走，直到叶子节点。

可以看到，B树 寻找最值的时间复杂度只和树的高度有关，而不是数据的个数，如果树的高度为 h，那么时间复杂度为 O(h)。只要树的 度(degree) 足够，每层能放的数据其实是很多的，那么树的高度就会很小，查询最值的时间复杂度也很小。

代码实现

internal class Node<TKey, TValue>
{
    public Item<TKey, TValue?> Max()
    {
        // 沿着右子树一直走，直到叶子节点，叶子节点的最大值就是最大值
        if (IsLeaf)
        {
            return _items[ItemsCount - 1];
        }

        return _children[ChildrenCount - 1].Max();
    }

    public Item<TKey, TValue?> Min()
    {
        // 沿着左子树一直走，直到叶子节点，叶子节点的最小值就是最小值
        if (IsLeaf)
        {
            return _items[0];
        }

        return _children[0].Min();
    }
}

BTree 类中，我们只需要调用根节点的 Max 和 Min 方法即可。

public sealed class BTree<TKey, TValue> : IEnumerable<KeyValuePair<TKey, TValue?>>
{
    public KeyValuePair<TKey, TValue?> Max()
    {
        if (_root == null)
        {
            throw new InvalidOperationException("BTree is empty.");
        }

        var maxItem = _root.Max();
        return new KeyValuePair<TKey, TValue?>(maxItem.Key, maxItem.Value);
    }

    public KeyValuePair<TKey, TValue?> Min()
    {
        if (_root == null)
        {
            throw new InvalidOperationException("BTree is empty.");
        }

        var minItem = _root.Min();
        return new KeyValuePair<TKey, TValue?>(minItem.Key, minItem.Value);
    }
}

B树的遍历

算法说明

B树的遍历和二叉树的遍历是相通的，都可以分为深度遍历和广度遍历。深度遍历又分为先序遍历、中序遍历和后序遍历。

本文将以中序遍历为例介绍 B树 的遍历，通过中序遍历可以对 B树 中的数据从小到大进行排序。

其他遍历方式的也都可以理解成 二叉树 遍历方式的拓展，有兴趣的读者朋友可以自行尝试实现一下。

不过，B树的遍历和二叉树的遍历还是有一些区别的，我们先来看一下二叉树的中序遍历。

二叉树的中序遍历分为下面几步：

1. 先遍历左子树。
2. 访问当前节点。
3. 遍历右子树。

在每个子树中，重复上面的步骤。

以下面的二叉树为例再次说明一遍：

1. 先遍历 8 的左子树 T1

2. 在 T1 中先遍历 4 的左子树 T2

3. 在 T2 中先遍历 2 的左子树，只有一个节点，直接访问 1，

4. 在 T2 中访问 2

5. 在 T2 中遍历 2 的右子树，只有一个节点，直接访问 3，T2 遍历完毕

6. 在 T1 中访问 4

7. 在 T1 中遍历 4 的右子树 T3

8. ... 以此类推，直到遍历完整棵树。
   
   

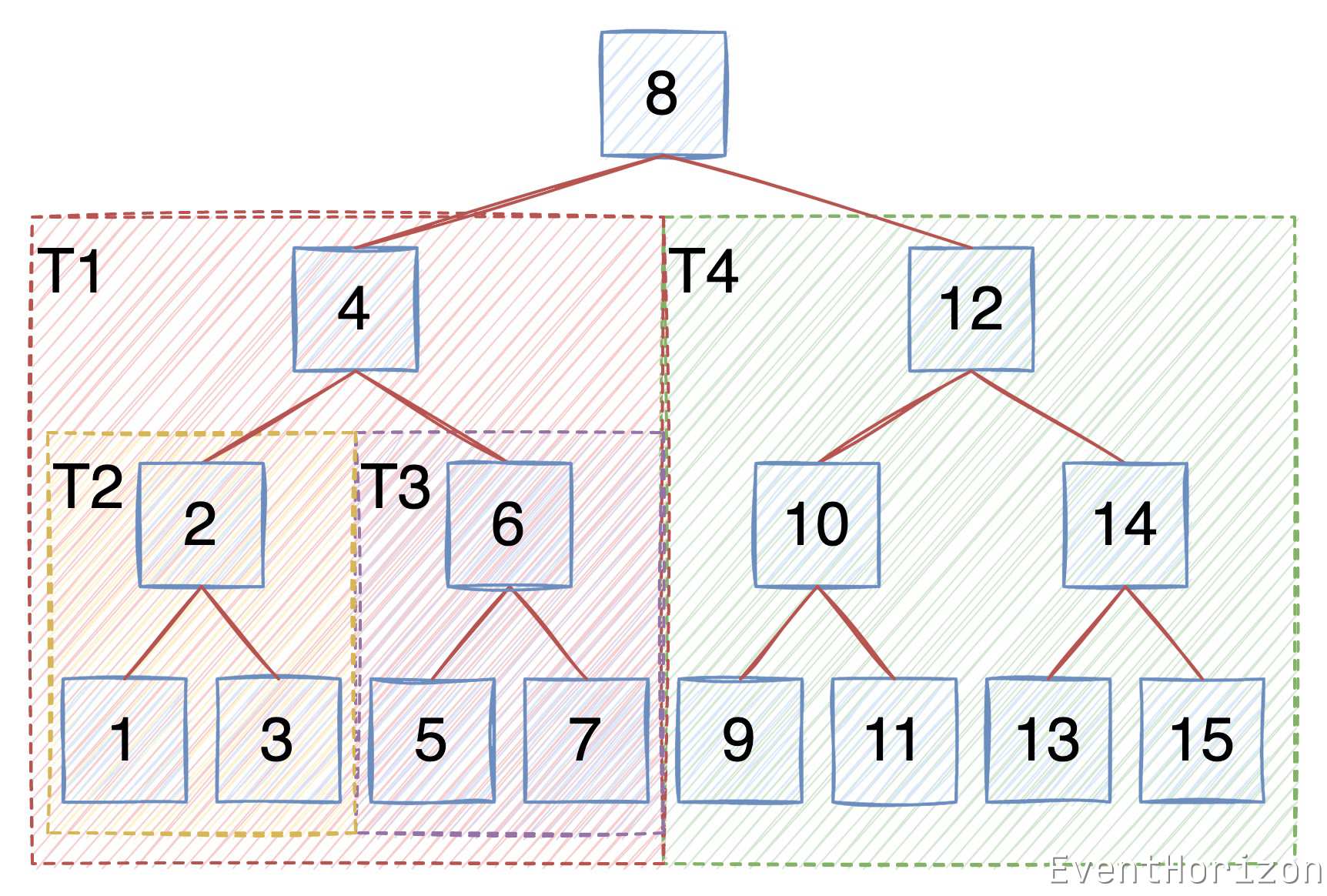
B树的中序遍历也是类似的，只不过 B树 的节点中有多个 Item 和 多个 子树，我们需要遍历每个 Item 的 左右子树以及 Item 。

B树的中序遍历分为下面几步：

1. 遍历节点中的第一个子树，也就是第一个 Item 的左子树。
2. 遍历节点中的第一个 Item。
3. 遍历节点中的第二个子树，也就是第一个 Item 的右子树。
4. 直至遍历完所有的 Item，遍历节点中的最后一个子树。

在每个子树中，重复上面的步骤。

如下图所示，我们以中序遍历的方式遍历 B树，会先遍历 3 的左子树，然后访问 3，再遍历 3 的右子树，直至遍历完 9 的右子树。

代码实现

遍历每个节点的 Item 和 子树，我们可以使用递归的方式实现，代码如下：

internal class Node<TKey, TValue>
{
    public IEnumerable<Item<TKey, TValue?>> InOrderTraversal()
    {
        var itemsCount = ItemsCount;
        var childrenCount = ChildrenCount;
        if (IsLeaf)
        {
            for (int i = 0; i < itemsCount; i++)
            {
                yield return _items[i];
            }

            yield break;
        }

        // 左右子树并不是相当于当前的 node 而言，而是相对于每个 item 来说的
        for (int i = 0; i < itemsCount; i++)
        {
            if (i < childrenCount)
            {
                foreach (var item in _children[i].InOrderTraversal())
                {
                    yield return item;
                }
            }

            yield return _items[i];
        }

        // 最后一个 item 的右子树
        if (childrenCount > itemsCount)
        {
            foreach (var item in _children[childrenCount - 1].InOrderTraversal())
            {
                yield return item;
            }
        }
    }
}

BTree 实现了 IEnumerable 接口，以便我们可以使用 foreach 循环来遍历 BTree 中的所有 Item，其代码只要调用 Node 的 InOrderTraversal 方法即可：

public sealed class BTree<TKey, TValue> : IEnumerable<KeyValuePair<TKey, TValue?>>
{
    public IEnumerator<KeyValuePair<TKey, TValue?>> GetEnumerator()
    {
        foreach (var item in _root!.InOrderTraversal())
        {
            yield return new KeyValuePair<TKey, TValue?>(item.Key, item.Value);
        }
    }

    IEnumerator IEnumerable.GetEnumerator()
    {
        return GetEnumerator();
    }
}

Benchmarks

最后，我们来看一下 Degree 对 BTree 的性能的影响。

注意，我们这里只考虑 B树的数据量远大于 Degree 的情况。

我们使用 BenchmarkDotNet 来测试，测试代码如下：

public class BTreeWriteBenchmarks
{
    [Params(2, 3, 4, 5, 6)] public int Degree { get; set; }

    private HashSet<int> _randomKeys;

    [GlobalSetup]
    public void Setup()
    {
        _randomKeys = new HashSet<int>();
        var random = new Random();
        while (_randomKeys.Count < 1000)
        {
            _randomKeys.Add(random.Next(0, 100000));
        }
    }

    [Benchmark]
    public void WriteSequential()
    {
        var bTree = new BTree<int, int>(Degree);
        for (var i = 0; i < 1000; i++)
        {
            bTree.Add(i, i);
        }
    }

    [Benchmark]
    public void WriteRandom()
    {
        var bTree = new BTree<int, int>(Degree);
        foreach (var key in _randomKeys)
        {
            bTree.Add(key, key);
        }
    }
}

public class BenchmarkConfig : ManualConfig
{
    public BenchmarkConfig()
    {
        Add(DefaultConfig.Instance);
        Add(MemoryDiagnoser.Default);

        ArtifactsPath = Path.Combine(AppContext.BaseDirectory, "artifacts", DateTime.Now.ToString("yyyy-mm-dd_hh-MM-ss"));
    }
}

new BenchmarkSwitcher(new[]
{
    typeof(BTreeReadBenchmarks),
}).Run(args, new BenchmarkConfig());

我们测试了 4 项性能指标，分别是顺序读、随机读、最小值、最大值、遍历，测试结果如下：

可以看到，在相同的数据量下，Degree 越大，性能越好，这是因为 Degree 越大，BTree 的高度越小，所以每次查找的时候，需要遍历的节点越少，性能越好。

但是不是真的 Degree 越大就越好呢，我们再来看下写入性能的测试结果：

public class BTreeWriteBenchmarks
{
    [Params(2, 3, 4, 5, 6)] public int Degree { get; set; }

    private HashSet<int> _randomKeys;

    [GlobalSetup]
    public void Setup()
    {
        _randomKeys = new HashSet<int>();
        var random = new Random();
        while (_randomKeys.Count < 1000)
        {
            _randomKeys.Add(random.Next(0, 100000));
        }
    }

    [Benchmark]
    public void WriteSequential()
    {
        var bTree = new BTree<int, int>(Degree);
        for (var i = 0; i < 1000; i++)
        {
            bTree.Add(i, i);
        }
    }

    [Benchmark]
    public void WriteRandom()
    {
        var bTree = new BTree<int, int>(Degree);
        foreach (var key in _randomKeys)
        {
            bTree.Add(key, key);
        }
    }
}

测试结果如下：

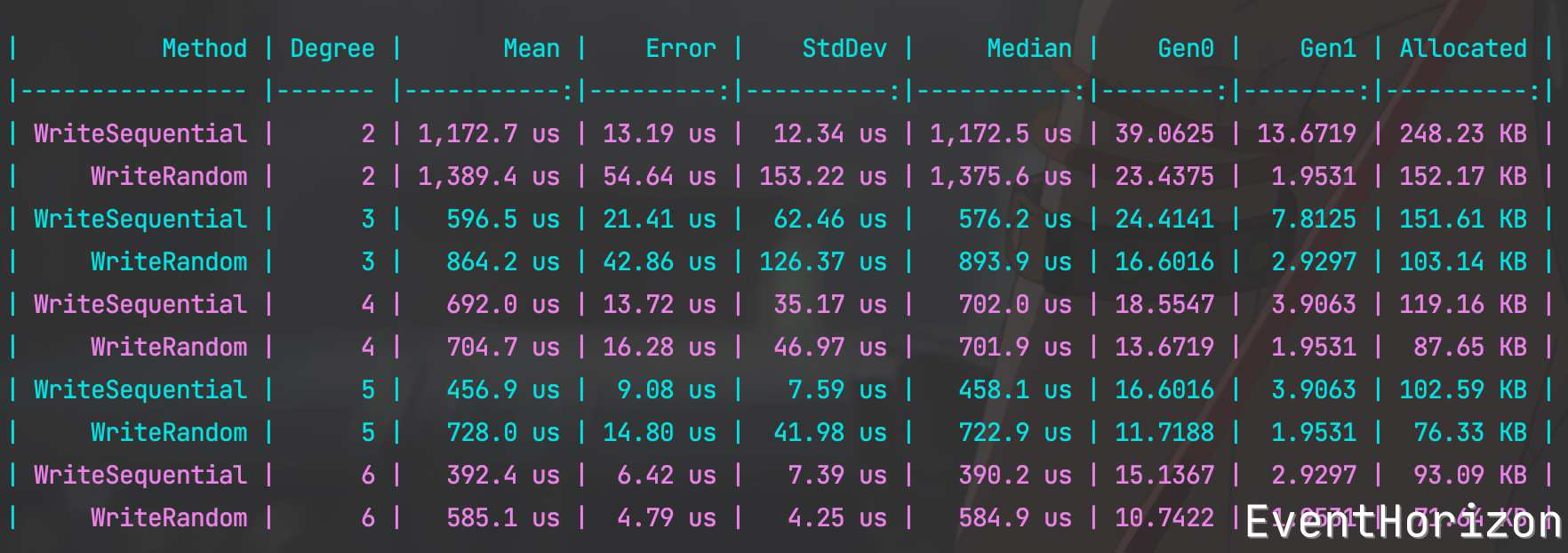
可以看到，Degree 越大，写入性能也越好，每个节点的容量够大，需要分裂的次数就变少了。

总结

• B树是一种多路平衡查找树，可以基于二分查找的思路来查询数据。
• B树的数据量远大于 Degree 的情况下，B树的 Degree 越大，读写性能越好。如果是磁盘中的实现，每个节点要考虑到磁盘页的大小，Degree 会有上限。

参考资料

Google 用 Go 实现的内存版 B树 https://github.com/google/btree