使用加强堆结构解决topK问题

作者：Grey

原文地址: 使用加强堆结构解决topK问题

题目描述

LintCode 550 · Top K Frequent Words II

思路

由于要统计每个字符串的次数，以及字典序，所以，我们需要把用户每次add的字符串封装成一个对象，这个对象中包括了这个字符串和这个字符串出现的次数。

假设我们封装的对象如下：

public class Word {
    public String value; // 对应的字符串
    public int times; // 对应的字符串出现的次数

    public Word(String v, int t) {
        value = v;
        times = t;
    }
}

topk的要求是： 出现次数多的排前面,如果次数一样，字典序小的排前面

很容易想到用有序表+比较器来做。

比较器的规则定义成和topk的要求一样，然后把元素元素加入使用比较器的有序表中，如果要返回topk，直接从这个有序表弹出返回给用户即可。比较器的定义如下：

public class TopKComparator implements Comparator<Word> {
    @Override
    public int compare(Word o1, Word o2) {
        // 次数大的排前面，次数一样字典序在小的排前面
        return o1.times == o2.times ? o1.value.compareTo(o2.value) : (o2.times - o1.times);
    }
}

有序表配置这个比较器即可

TreeSet<Word>  topK = new TreeSet<>(new TopKComparator());

所以topk()方法很简单，只需要从有序表里面把元素拿出来返回给用户即可

public List<String> topk() {
      List<String> result = new ArrayList<>();
      for (Word word : topK) {
          result.add(word.value);
      }
      return result;
}

时间复杂度 O(K)

以上步骤不复杂，接下来是add的逻辑，add的每次操作都有可能对前面我们设置的topK有序表造成影响，

所以在每次add操作的时候需要有一个机制可以告诉topK这个有序表，需要淘汰什么元素，需要新加哪个元素，让topK这个有序表时时刻刻只存topk个元素，

这样就可以确保topK()方法比较单纯，时间复杂度保持在O(K)

所以接下来的问题是：如何告诉topK这个有序表，需要淘汰什么元素，需要新加哪个元素?

我们可以通过堆来维持一个门槛，堆顶元素表示最先要淘汰的元素，所以堆中的比较策略定为：

次数从小到大，字典序从大到小，这样，堆顶元素永远是：次数相对更少或者字典序相对更大的那个元素。所以如果某个时刻要淘汰一个元素，从堆顶拿出来，然后再到topK这个有序表中查询是否有这个元素，有的话就从topK这个有序表中删除这个元素即可。

private class ThresholdComparator implements Comparator<Word> {

    @Override
    public int compare(Word o1, Word o2) {
        // 设置堆门槛，堆顶元素最先被淘汰
        return o1.times == o2.times ? o2.value.compareTo(o2.value) : (o1.times - o2.times);
    }
}

如果使用Java自带的PriorityQueue做这个堆，无法实现动态调整堆的功能，因为我们需要把次数增加的字符串（Word）在堆上动态调整，自带的PriorityQueue无法实现这个功能，PriorityQueue只能支持每次新增或者删除一个节点的时候，动态调整堆(
O(logN)，但是如果堆中的节点变化了，PriorityQueue无法自动调整成堆结构，所以我们需要实现一个增强堆，用于节点变化的时候可以动态调整堆结构(保持O(logN)复杂度)。

加强堆的核心是增加了一个哈希表，

private Map<Word, Integer> indexMap;

用于存放每个节点所在堆上的位置，在节点变化的时候，可以通过哈希表查出这个节点所在的位置，然后从所在位置进行heapify/heapInsert操作，且这两个操作只会走一个,
这样就动态调整好了这个堆结构，以下resign方法就是完成这个工作

public void resign(Word word) {
    int i = indexMap.get(word);
    heapify(i);
    heapInsert(i);
}

除了这个resign方法，自定义堆中的其他方法和常规的堆没有区别，在每次进行heapify和heapInsert操作的时候，如果涉及到交换两个元素，需要将indexMap中的两个元素的位置也互换

private void swap(int i, int j) {
 if (i != j) {
  indexMap.put(words[i], j);
  indexMap.put(words[j], i);
  Word tmp = words[i];
  words[i] = words[j];
  words[j] = tmp;
 }
}

由于自定义堆和有序表topk只存top k个数据，所以TopK结构中还需要一个哈希表来记录所有的字符串出现与否：

private Map<String, Word> map;

自此，TopK结构中的add方法需要的前置条件已经具备，整个add方法的流程如下：

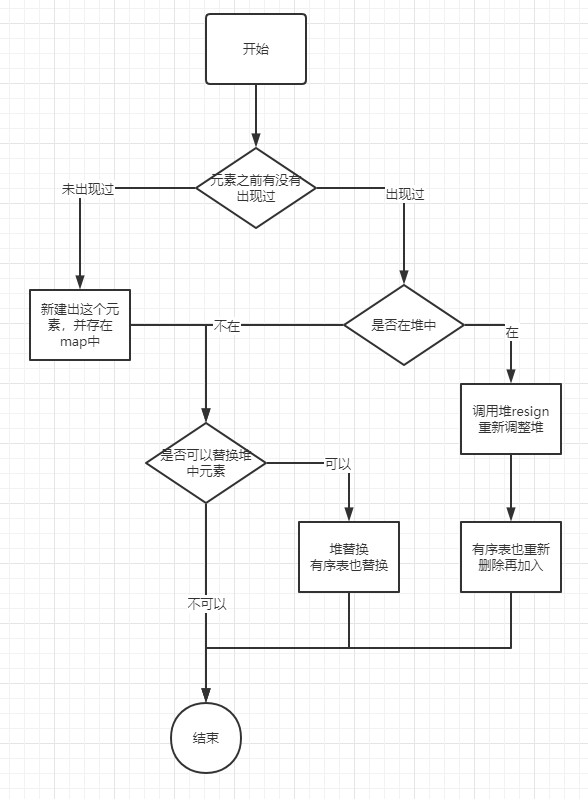
关于复杂度，add方法，时间复杂度O(log K), topk方法，时间复杂度O(K)。

完整代码

class TopK {
    private TreeSet<Word> topK;
    private Heap heap;
    private Map<String, Word> map;
    private int k;

    public TopK(int k) {
        this.k = k;
        topK = new TreeSet<>(new TopKComparator());
        heap = new Heap(k, new ThresholdComparator());
        map = new HashMap<>();
    }

    public void add(String str) {
        if (k == 0) {
            return;
        }
        Word word = map.get(str);
        if (word == null) {
            // 新增元素
            word = new Word(str, 1);
            // 是否到达门槛可以替换堆中元素
            if (heap.isReachThreshold(word)) {
                if (heap.isFull()) {
                    Word toBeRemoved = heap.poll();
                    topK.remove(toBeRemoved);
                }
                heap.add(word);
                topK.add(word);
            }
        } else {
            if (heap.contains(word)) {
                topK.remove(word);
                word.times++;
                topK.add(word);
                heap.resign(word);
            } else {
                word.times++;
                if (heap.isReachThreshold(word)) {
                    if (heap.isFull()) {
                        Word toBeRemoved = heap.poll();
                        topK.remove(toBeRemoved);
                    }
                    heap.add(word);
                    topK.add(word);
                }
            }
        }
        map.put(str, word);
    }

    public List<String> topk() {
        if (k == 0) {
            return new ArrayList<>();
        }
        List<String> result = new ArrayList<>();
        for (Word word : topK) {
            result.add(word.value);
        }
        return result;
    }

    private class Word {
        public String value;
        public int times;

        public Word(String v, int t) {
            value = v;
            times = t;
        }
    }

    private class TopKComparator implements Comparator<Word> {
        @Override
        public int compare(Word o1, Word o2) {
            // 次数大的排前面，次数一样字典序在小的排前面
            return o1.times == o2.times ? o1.value.compareTo(o2.value) : (o2.times - o1.times);
        }
    }

    private class ThresholdComparator implements Comparator<Word> {

        @Override
        public int compare(Word o1, Word o2) {
            // 设置堆门槛，堆顶元素最先被淘汰
            return o1.times == o2.times ? o2.value.compareTo(o1.value) : (o1.times - o2.times);
        }
    }

    private class Heap {
        private Word[] words;
        private Comparator<Word> comparator;
        private Map<Word, Integer> indexMap;

        public Heap(int k, Comparator<Word> comparator) {
            words = new Word[k];
            indexMap = new HashMap<>();
            this.comparator = comparator;
        }

        public boolean isEmpty() {
            return indexMap.isEmpty();
        }

        public boolean isFull() {
            return indexMap.size() == words.length;
        }

        public boolean isReachThreshold(Word word) {
            if (isEmpty() || indexMap.size() < words.length) {
                return true;
            } else {
                if (comparator.compare(words[0], word) < 0) {
                    return true;
                }
                return false;
            }
        }

        public void add(Word word) {
            int size = indexMap.size();
            words[size] = word;
            indexMap.put(word, size);
            heapInsert(size);

        }

        private void heapify(int i) {
            int size = indexMap.size();
            int leftChildIndex = 2 * i + 1;
            while (leftChildIndex < size) {
                Word weakest = leftChildIndex + 1 < size
                        ? (comparator.compare(words[leftChildIndex], words[leftChildIndex + 1]) < 0
                        ? words[leftChildIndex]
                        : words[leftChildIndex + 1])
                        : words[leftChildIndex];
                if (comparator.compare(words[i], weakest) < 0) {
                    break;
                }
                int weakestIndex = weakest == words[leftChildIndex] ? leftChildIndex : leftChildIndex + 1;
                swap(weakestIndex, i);
                i = weakestIndex;
                leftChildIndex = 2 * i + 1;
            }
        }

        public void resign(Word word) {
            int i = indexMap.get(word);
            heapify(i);
            heapInsert(i);
        }

        private void heapInsert(int i) {
            while (comparator.compare(words[i], words[(i - 1) / 2]) < 0) {
                swap(i, (i - 1) / 2);
                i = (i - 1) / 2;
            }
        }

        public boolean contains(Word word) {
            return indexMap.containsKey(word);
        }

        public Word poll() {
            Word result = words[0];
            swap(0, indexMap.size() - 1);
            indexMap.remove(result);
            heapify(0);
            return result;
        }

        private void swap(int i, int j) {
            if (i != j) {
                indexMap.put(words[i], j);
                indexMap.put(words[j], i);
                Word tmp = words[i];
                words[i] = words[j];
                words[j] = tmp;
            }
        }
    }
}

更多

算法和数据结构笔记

参考资料

算法和数据结构体系班-左程云