2021.05.14 tarjan

2021.05.14 tarjan

标准版tarjan

这里使用数组来模拟栈

void tarjan(int x){
	++ind;
	dfn[x]=low[x]=ind;
	stacki[++top]=x;
	instack[x]=true;
	for(int i=head[x];i;i=a[i].next ){
		int v=a[i].to ;
		if(dfn[v]==0){
			tarjan(v);
			low[x]=min(low[x],low[v]);
		}else if(instack[v]){
			low[x]=min(low[x],dfn[v]);//此处可改为low[x]=min(low[x],low[v]);原因如下解释
		}
		//建议加上if(instacki[v]),否则不在栈中的元素且dfn已更新过的元素会被再一次更新
	}
	int k=0;
	if(dfn[x]==low[x]){
		++cnt;
		do{
			k=stacki[top];
			--top;
			++num[cnt];
			instack[k]=false;
			belong[k]=cnt;
		}while(k!=x);
	}
}
//luougu 2341

直接使用STL

void tarjan(int x){
	++ind;
	low[x]=dfn[x]=ind;
	stacki.push(x);
	vis[x]=1;
	for(int i=head[x];i;i=a[i].next ){
		int v=a[i].to ;
		if(!dfn[v]){
			tarjan(v);
			low[x]=min(low[x],low[v]);
		}else if(vis[v]){
			low[x]=min(low[x],low[v]);//此处可改为low[x]=min(low[x],dfn[v]);
		}
	}
	int k=0;
	if(low[x]==dfn[x]){
		do{
			k=stacki.top();
			stacki.pop() ;
			vis[k]=0;
			bl[k]=x;
		}while(k!=x);
	}
}

缩点

在找到每个点属于哪一个强连通分量以后再建一个图就成，以下为主要代码：

void addi(int u,int v){
	++cnt;
	ai[cnt].from =u;
	ai[cnt].to =v;
	ai[cnt].next =headi[u];
	headi[u]=cnt;
	++in[v];
}
void tarjan(int x){
	++ind;
	low[x]=dfn[x]=ind;
	stacki.push(x);
	vis[x]=1;
	for(int i=head[x];i;i=a[i].next ){
		int v=a[i].to ;
		if(!dfn[v]){
			tarjan(v);
			low[x]=min(low[x],low[v]);
		}else if(vis[v]){
			low[x]=min(low[x],dfn[v]);
		}
	}
	int k=0;
	if(low[x]==dfn[x]){
		do{
			k=stacki.top();
			stacki.pop() ;
			vis[k]=0;
			bl[k]=x;
			sum[x]+=num[k];//题目需要，可删
		}while(k!=x);
	}
}
int main(){
	//中间省略
	for(int i=1;i<=n;i++){
		if(!dfn[i])tarjan(i);
	}
	cnt=0;
	for(int i=1;i<=m;i++){
		if(bl[a[i].from ]!=bl[a[i].to ]){
			addi(bl[a[i].from ],bl[a[i].to ]);
		}
	}
	//中间省略
	return 0;
}
//luogu 3387

割点

定义：在一个无向图中，如果去掉一个点和它所连出去的的所有边，使得剩下的点不联通（即分成一个以上的强连通分量）时，这个点被称为关节点。关节点也就是割点。

对于根节点：

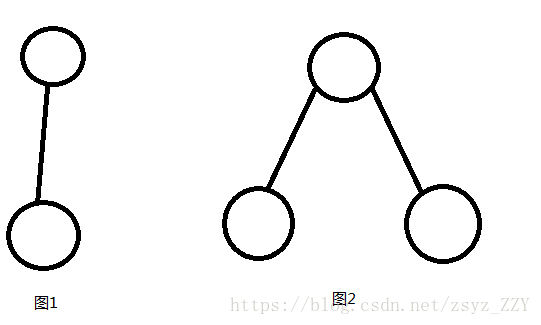
如图1，当根节点只有一个儿子时，割掉它，剩下的点必然联通，且新的树的个节点为它的儿子；

如图2，当根节点有两个儿子时，割掉它，剩下的点必然不联通（有两个强连通分量）。

对于非根节点：

如图3，点v1,v2均为点u的儿子，我们可以发现（手动模拟，v1和v2不联通），点u为割点。

此时点u存在一个可遍历到的后代v1，且点v1无法走回点u的前辈，满足该性质。

我们在v1,v2间加上一条边。

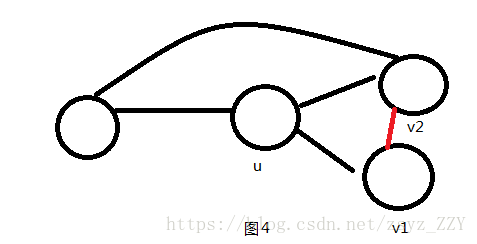
如图4，此时我们可以发现点u并不为割点（此时v1,v2和点u的前辈联通）。

此时点u存在一个可遍历到的后代v1，且点v1,v2都可以走回点u的前辈，不满足该性质。

来自割点详解_zsyz_ZZY的博客-CSDN博客_割点

void tarjan(int x,int root){
	int child=0;
	++ind;
	low[x]=dfn[x]=ind;
	for(int i=head[x];i;i=a[i].next ){
		int v=a[i].to ;
		if(!dfn[v]){
			tarjan(v,x);
			low[x]=min(low[x],low[v]);
			if(low[v]>=dfn[x]&&x!=root)cut[x]=1;
			if(x==root)++child;
		}
		low[x]=min(low[x],dfn[v]);//此处不可以改为low[x]=min(low[x],low[v]);解释如下
	}
	if(root==x&&child>=2)cut[x]=1;
}
int main(){
//中间省略
	for(int i=1;i<=n;i++)
		if(!dfn[i])tarjan(i,i);
	for(int i=1;i<=n;i++)
		if(cut[i])++ans;
//中间省略
}
//luogu 3388

关于low[x]=min(low[x],low[v])和low[x]=min(low[x],dfn[x])的问题

标准版tarjan和缩点需要判断点在不在强连通分量中以及在哪个强连通分量中，所以一个点可以重复更新low[x]=min(low[x],dfn[v])，如果在同一个强连通分量中，迟早会遍历到起点，况且instacki[]或vis[]数组就是为了判断这个点在不在栈中。

而割点只需要寻到这个点能到达的且不是从来时的边到达的最早的节点，这个最早的节点可以和另一个更早的节点相连，设最早的节点为fa,更早的节点为grandpa,这个节点为son，则low[fa]==low[grandpa]&&dfn[fa]!=dfn[grandpa]，我们只需要使low[son]=dfn[fa]而不是使low[x]=low[grandpa]。

参考题解 P3388 【【模板】割点（割顶）】 - Michael_Li 的博客 - 洛谷博客 (luogu.com.cn)