道长的算法笔记：KMP算法及其各种变体

(一)如何优化暴力算法

Waiting...

(二)KMP模板

　KMP 算法的精髓在于 \(next\) 数组，\(next[i]=j\) 代表 \(p[1,j]=p[i-j+1,i]\)，\(next[i]\) 数值意义代表 \(p[1,i]\) 所有前缀与后缀的最长公共部分，我们约定本文提到的前缀与后缀均为不包含原字符串 \(p\) 本身。

　这个过程动手计算并不困难，但想理解代码为何如此实现倒并不简单。个人建议，自行动手画图计算 \(next\) 数组，以此体会这个过程，否则永远不可能理解哪怕一行代码。由于 \(next\) 可能会有命名与内置命名冲突的风险，因而我们的代码实现中写为 \(nxt\) 而非 \(next\)，下文我们都将使用 \(nxt\)，同时为使代码实现起来更加简洁，我们所有字符串的索引均从 \(1\) 开始计算。

　说完约定之后，接着来看模式串 \(p\) 的最长前缀与后缀公共长度的计算过程，前缀字符最大可取到的范围是在 \(s[1,n-2]\)，后缀最大可取到的范围是在 \(s[2,n-1]\)，例如 \(abcd\) 前缀包括\(\{a、ab、abc\}\)，后缀包括了\(\{d、cd、bcd\}\)，值得注意，后缀的字符出场顺序与原字符串 \(p\) 是一样的，都是从左往右。回忆一下 \(nxt[i] = j\)，其含义是指 \(p[1,j]=p[i-j+1,i]\)，注意，此处使用方括号与逗号分隔的表示法是指左闭右闭区间，使用方括号与冒号分隔的切片表示法才是左闭右开区间。我们计算 \(nxt\) 数组的过程其实就是字符串 \(p\) 对其自身的匹配过程，我们错开一位再进行比较即可比对所有前缀与所有后缀之间，最大公共长度部分了。

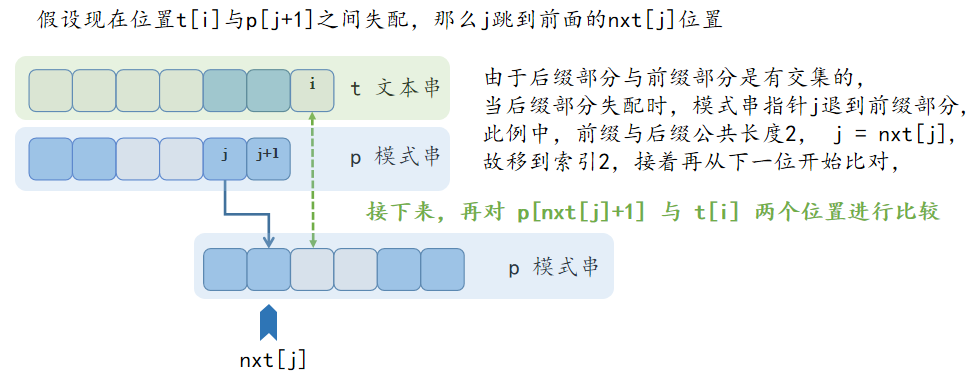
　再看上图的匹配过程，如果失配，指向模式串的指针 \(p\) 往左退，除非已经到达了退无可退的状态，方才跳出。在完成了向左移动退步的操作之后，再对当前文本串 \(t[i]\) 位置与模式串进行对比，指针 \(i\) 从始至终都只向右移动。下列模板来自 ACwing831 ，若条件允许，强烈建议购买 ACwing 算法课程，其它模板题亦有 LeetCode28、洛谷3375等等。

#include<bits/stdc++.h>
using namespace std;

#define MAXN 1000010

char txt[MAXN], pat[MAXN];

int nxt[MAXN];
int  main(){
    int n, m;
    scanf("%d %s", &n, pat + 1);
    scanf("%d %s", &m, txt + 1);
    // 显然i = 1不符合条件，此时即既没有非平凡前缀又没有非平凡后缀
    for(int i = 2, j = 0; i <= n; i++){
        while(j && pat[i] != pat[j + 1])
            j = nxt[j];
        if(pat[i] == pat[j + 1]) j++;
        nxt[i] = j;
    }
    for(int i = 1, j = 0; i <= m; i++){
        while(j && txt[i] != pat[j + 1])
            j = nxt[j];
        if(txt[i] == pat[j + 1]) j++;
        if(j == n){
            printf("%d ", i - n);
            j = nxt[j];
        }
    }
    printf("\n");
    return 0;
}

　KMP 算法的本质是利用字符串本身蕴含的冗余信息，通俗来说就是利用自身的相同部分来减少比对的次数，很直观的，当出现失配的时候，对于已经比过的、相同的部分，我们显然不需要重新再比对一次。

　当一个字符串是由某个循环节，循环若干次构成的时候，此时字符串蕴含的冗余信息几乎是最理想的状态，KMP 认为所有的字符串均是通过某个循环节，进行若干次循环之后，再截取子串获得的，例如字符串 \(cabcabca\) 其实就是通过 \(abc\) 循环四次之后所得的 文本串\(txt\) 截取 \(txt[3,10]\) 部分得到的。下文“KMP理解加深”章节中，我们会继续讨论这一点。

(三)KMP理解加深

(3.1)重复的子字符串问题

　给定一个非空的字符串 \(s\) ，检查 \(s\) 是否可以通过由其一个子串重复多次构成，假如 \(s\) 包含若干子串 \(x\)，不妨记 \(s=kx\)，其中 \(k>=2\)，那么 \(s+s=2kx\)，掐头去尾丢弃两个字符，也就是相当于破坏了头尾部分两个 \(x\) 子串，此番操作之后，剩余 \(2(k-1)x\)，由于 \(k>=2\)，代入可知 \(s\) 至少会在 \(2(k-1)x\) 出现一次，因而只要对于切片 \(2s[1:-1]\) 检查是否包含 \(s\) 即可知道 \(s\) 是否可以通过由其一个子串重复多次构成。

class Solution {
public:
    bool repeatedSubstringPattern(string s) {
        string cp = "#" + s;
        string txt = "#" + s.substr(1) + s; txt.pop_back();
        vector<int> nxt(cp.size() + 1, 0);
        for(int i = 2, j = 0; i < cp.size(); i++){
            while(j && cp[i] != cp[j + 1])
                j = nxt[j];
            if(cp[i] == cp[j + 1]) j++;
            nxt[i] = j;
        }
        for(int i = 1, j = 0; i < txt.size(); i++){
            while(j && txt[i] != cp[j + 1])
                j = nxt[j];
            if(txt[i] == cp[j + 1]) j++;
            if(j == cp.size() - 1){
                return true;
            }
        }
        return false;
    }
};

　这道题是比较简单的面试题，检查字符串是否可由多个重复的子串构成，本题放在此处主要是为了下一题分析字符串子串循环节长度、循环次数做铺垫。

　为了便于形式化表达，我们不妨使用记号 \(nxt^2[j]\) 代表 \(nxt[nxt[j]]\)，以此类推，我们可以写出 \(nxt^k[j]\), 其中 \(k\)是整数，且不大于 \(n-1\)，这种形式化的表达会在下文帮助我们理解 KMP 算法的本质。

(3.2)串周期

　给定一个字符串，其前缀是从第一个字符开始的连续若干个字符，在本例中，我们规定前缀包括字符串本身，例如 \(abaab\) 共有前缀 \(\{a，ab，aba，abaa，abaab\}\)，我们希望对每个前缀\(s[1,i]，(i>1)\)判断是否具有循环节，如果存在循环节，其长度是多少，循环次数是多少。

　对于某一个字符串\(s[1,i]\)，在其众多的 \(nxt[1...i]\) 候选项中，如果存在于一个\(nxt[x],x\in[1...i]\)使得 \(i\%i - nxt[x] = 0\), 那么\(s[1,i-nxt[x]]\), 也即第二行图例中的灰色部分，即为 \(s[1,i]\) 循环元，其循环次数 \(K=i/(i-nxt[x])\)。

　其实，只要 \(s[1,i]\) 是由若干循环节构成的，那么我们要找的 \(nxt[x]\) 其实就是 \(nxt[i]\)，因为 \(nxt[i]\) 代表着 “失配时指针向左移动最少的位置”，如果存在其它 \(nxt[x]，x \neq i\) 同样满足 \(i\%i - nxt[x] = 0\)，则其需要移动的位置一定多于 \(nxt[i]\)，也就是说，此时的 \(i-nxt[x]\) 并非最小单元长度。

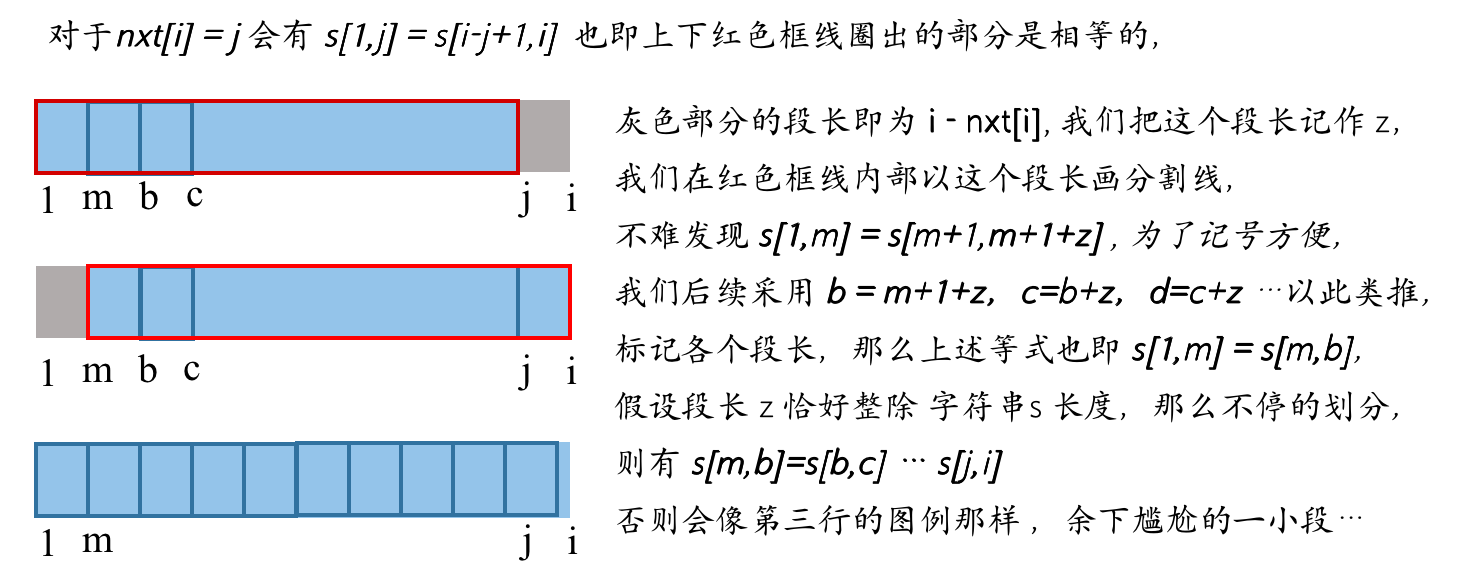
　举个例子，比如字符串 \(abababab\)，最小的循环节应为 \(ab\)，长度\(2\)，满足\(8\%2=0\)，但是 \(abab\) 长度\(4\)，也能构成一个循环节，同样满足 \(8\%4=0\)，但它并非最小循环节。

#include <bits/stdc++.h>
#include <algorithm>
using namespace std;

char str[1000010];
int nxt[1000010];

int n;
int kase;
int main(){
    while(scanf("%d", &n) != EOF){
        if(n == 0) break;
        scanf("%s", str + 1);
        for(int i  = 2, j =0; i <= n; i++){
            while(j && str[i] != str[j + 1])
                j = nxt[j];
            if(str[i] == str[j + 1]){
                j++;
            }
            nxt[i] = j;
        }
        printf("Test case #%d\n", ++kase);
        for(int i = 2; i <= n; i++){
            if(i % (i - nxt[i]) == 0 && nxt[i]){
                printf("%d %d\n", i, i/(i - nxt[i]));
            }
        }
        printf("\n");
    }
    return 0;
}

　本题能够延伸得到一些其它结论，详见下列条目，其中 \(x\) 代表的含义与上文相同：

• 如果\(i-nxt[i]\) 能够整除 \(i\)，那么\(s[1,i]\)具有最小循环节，长度 \(i-nxt[i]\)
• 如果\(i-nxt[x]\)，(\(x>0\) 且 \(x \neq i)\) 能够整除 \(i\)，那么\(s[1,i]\) 具有循环元，长度 \(i-nxt[x]\)
• 其余候选项 \(nxt[x]\) 均满足 \(x > 0, x = nxt^k[i]\)，其中 \(k=1,2,3,4...n-1\)
• 任意一个循环元的长度必然是最小循环元的整数倍
• 如果 \(i-nxt[i]\) 无法整除 \(i\)，那么任意 \(i-nxt[x]\) 均不可能作为 \(s[1,i]\) 循环元
• 无论 \(m=i-nxt[i]\) 可否整除 \(i\)，\(i-nxt[x]\) 都等于若干倍 \(m\)，也即 \(i-nxt[x]=bm\)

　对于最后一条可能的会使得感到抽象，我们举个例子。使用的 \(abc\) 作为循环节反复拼接四次构成新字符串 \(abcabcabcabc\)，然后截取其中一个片段 \(cabcabca\) 作为我们接下来分析的文本串\(txt\)，我们先算这个片段 \(nxt\) 数组。

　显然文本串 \(txt\) 没有循环节，但是 \(8-nxt[8]=3\)，所得的数值 \(3\) 竟然就是我们最初用于构造的 \(txt\) 循环节的长度，\(8-nxt^2[8]=6\)，所得数值恰好是循环节的两倍，符合我们上面所说的规律，这是巧合吗？我们接着往下迭代，由于 \(nxt^3[8]=0\) 已经不在候选项中了，我们不再往下分析。其实，上述的过程其实并非巧合，相反其恰恰道出了 KMP 算法的本质，也即所有字符串均可通过循环节进行若干次循环之后截取子串得到。通常 \(i-nxt[i]\) 即可推算得出用于构造 \(s[1,i]\) 文本串的循环节长度。理解了这点，也就不难做出 AC4188连接字符串 、UVA10298这几道题了。

(3.3)匹配统计

Waiting...

(3.4)处理字符矩阵

Waiting...

(四)KMP算法变体

(4.1)构造Z函数求解LCP

Waiting...

(4.2)自动机模型

Waiting...

支持作者