Python 图_系列之基于<链接表>实现无向图最短路径搜索

图的常用存储方式有 2 种：

• 邻接炬阵

• 链接表

邻接炬阵的优点和缺点都很明显。优点是简单、易理解，对于大部分图结构而言，都是稀疏的，使用炬阵存储空间浪费就较大。

链接表的存储相比较邻接炬阵，使用起来更方便，对于空间的使用是刚好够用原则，不会产生太多空间浪费。操作起来，也是简单。

本文将以链接表方式存储图结构，在此基础上实现无向图最短路径搜索。

1. 链接表

链接表的存储思路：

使用链接表实现图的存储时，有主表和子表概念。

• 主表： 用来存储图对象中的所有顶点数据。
• 子表： 每一个顶点自身会维护一个子表，用来存储与其相邻的所有顶点数据。

如下图结构中有 5 个顶点，使用链接表保存时，会有主表 1 张，子表 5 张。链接表的优点是能够紧凑地表示稀疏图。

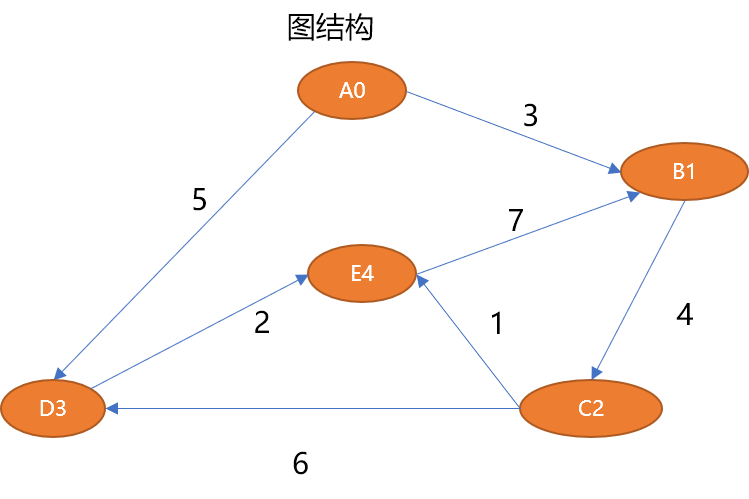
在 Python 中可以使用列表嵌套实现链接表，这应该是最简单的表达方式。

g = [
    ['A0', [('B1', 3), ('D3', 5)]],
    ['B1', [('C2', 4)]],
    ['C2', [('D3', 6), ('E4', 1)]],
    ['D3', [('E4', 2)]],
    ['E4', [('B1', 7)]],
]

在此基础上，可以做一些简单的常规操作。

查询所有顶点：

for node in g:
    print(node[0],end=' ')

查询顶点及其相邻顶点：

for node in g:
    print('-------------------')
    print(node[0], ":", end='')
    edges = node[1]
    for e in edges:
        v, w = e
        print(v, w, end=';')
    print()

当顶点和相邻顶点之间的关系很复杂时，这种层层嵌套的存储格式会让人眼花缭乱。即使要使用这种嵌套方式，那也应该选择 Python 中的字典类型，对于查询会方便很多。

g = {
    'A0':{'B1': 3, 'D3': 5},
    'B1': {'C2': 4},
    'C2': {'D3': 6, 'E4': 1},
    'D3': {'E4':2},
    'E4': {'B1': 7}
}

如上结构，在查询时，无论是方便性还是性能，都要强于完全的列表方案。

查询所有顶点：

for node in g.keys():
    print(node,end=" ")

查询与某一顶点相邻的顶点时，只需要提供顶点名称就可以了。

print("查询与 A0 项点有连接的其它顶点")
for k, v in g.get('A0').items():
    print((k, v), end=";")

以上的存储方案，适合于演示，并不适合于开发环境，因顶点本身是具有特定的数据含义（如，可能是城市、公交车站、网址、路由器……），且以上存储方案让顶点和其相邻顶点的信息过度耦合，在实际运用时，会牵一发而动全身。

也许一个微不足道的修改，会波动到整个结构的更新。

所以，有必要引于 OOP 设计理念，让顶点和图有各自特定数据结构，通过 2 种类类型可以更好地体现图是顶点的集合，顶点和顶点之间的多对多关系。

项点类：

class Vertex:
    def __init__(self, name, v_id=0):
        # 顶点的编号
        self.v_id = v_id
        # 顶点的名称
        self.v_name = name
        # 是否被访问过:False 没有 True:有
        self.visited = False
        # 与此顶点相连接的其它顶点
        self.connected_to = {}

顶点类结构说明：

• visited：用于搜索路径算法中，检查节点是否已经被搜索过。
• connected_to：存储与项点相邻的顶点信息。这里使用了字典，以顶点为键，权重为值。

图类：

class Graph:

    def __init__(self):
        # 一维列表，保存节点
        self.vert_list = {}
        # 顶点个数
        self.v_nums = 0
        # 使用队列模拟队列或栈，用于路径搜索算法
        self.queue_stack = []
        # 保存搜索到的路径
        self.searchPath = []

图类结构说明：

• queue_stack：使用队列模拟栈或队列。用于路径搜索过程中保存临时数据。

怎么使用列表模拟队列或栈？

列表有 append()、pop() 2 个很价值的方法。

append() 用来向列表中添加数据，且每次都是从列表最后面添加。

pop() 默认从列表最后面删除且弹出数据， pop(参数) 可以提供索引值用来从指定位置删除且弹出数据。

使用 append() 和 pop() 方法就能模拟栈，从同一个地方进出数据。

使用 append() 和 pop(0) 方法就能模拟队列，从后面添加数据，从最前面获取数据

• searchPath：用于保存搜索到的路径数据。

2. 最短路径算法

从图结构可知，从一个顶点到达另一个顶点，可不止一条可行路径，在众多路径我们总是试图选择一条最短路径，当然，需求不同，衡量一个路径是不是最短路径的标准也会不同。

如打开导航系统后，最短路径可能是费用最少的那条，可能是速度最快的那条，也可能是量程数最少的或者是红绿灯是最少的……

在无向图中，以经过的边数最少的路径为最短路径。

在有向加权图中，会以附加在每条边上的权重的数据含义来衡量。权重可以是时间、速度、量程数……

2.1 无向图最短路径算法

查找无向图中任意两个顶点间的最短路径长度，可以直接使用广度搜索算法。如下图求解 A0 ~ F5 的最短路径。

Tips： 无向图中任意 2 个顶点间的最短路径长度由边数决定。

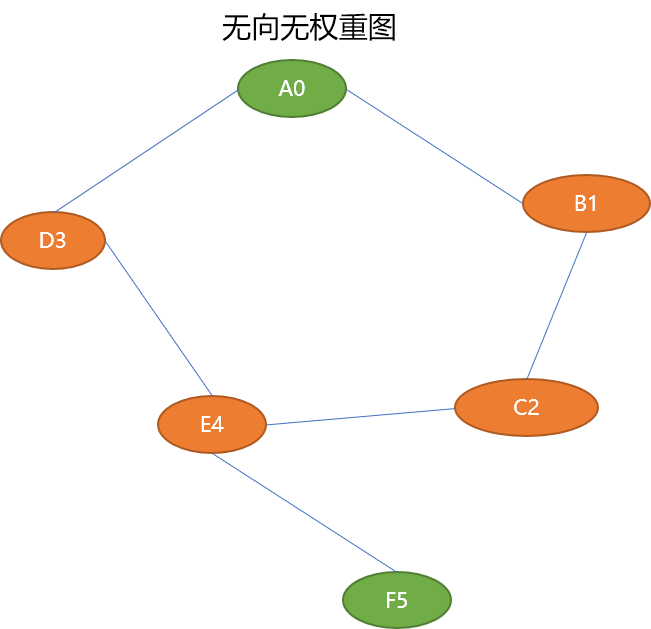
广度优先搜索算法流程：

广度优先搜索算法的基本原则：以某一顶点为参考点，先搜索离此顶点最近的顶点，再搜索离最近顶点最近的顶点……以此类推，一层一层向目标顶点推进。

如从顶点 A0 找到顶点 F5。先从离 A0 最近的顶点 B1、D3 找起，如果没找到，再找离 B1、D3 最近的顶点 C2、E4，如果还是没有找到，再找离 C2、E4 最近的顶点 F5。

因为每一次搜索都是采用最近原则，最后搜索到的目标也一定是最近的路径。

也因为采用最近原则，所以搜索过程中，在搜索过程中所经历到的每一个顶点的路径都是最短路径。最近+最近，结果必然还是最近。

显然，广度优先搜索的最近搜索原则是符合先进先出思想的，具体算法实施时可以借助队列实现整个过程。

算法流程：

• 先确定起始点 A0。

• 找到 A0 的 2 个后序顶点 B1 、D3 （或者说 B1、D3的前序顶点是 A0），压入队列中。除去起点 A0，B1、D3 顶点属于第一近压入队列的节点。

  B1 和 D3 压入队列的顺序并不影响 A0 ~B1 或 A0 ~ D3 的路径距离（都是 1）。

  A0~B1 的最短路径长度为 1

  A0~D3 的最短路径长度为 1

• 从队列中搜索 B1 时，找到 B1 的后序顶点 C2 并压入队列。B1 是 C2 的前序顶点。

  B1 ~ C2 的最短路径长度为 1，而又因为 A0~B1 的最短路径长度为 1 ，所以 A0 ~ C2 的最短路径为 2

• B1 搜索完毕后，在队列中搜索 B3 时，找到 B3 的后序顶点 E4 ，压入队列。因 B1 和 D3 属于第一近顶点，所以这 2 个顶点的后序顶点 C2、E4 属于第二近压入队列，或说 A0-B1-C2、A0-D3-E4 的路径距离是相同的（都为 2）。

• 当搜索到 C2 时，没有后序顶点，此时队列没有压入操作。

• 当 搜索到 E4 时，E4 有 2 个后序顶点 C2、F5，因 C2 已经压入过，所以仅压入 F5。因 F5 是由第二近顶点压入，所以 F5 是属于第三近压入顶点。

  A0-D3-E4-F5 的路径为 3。

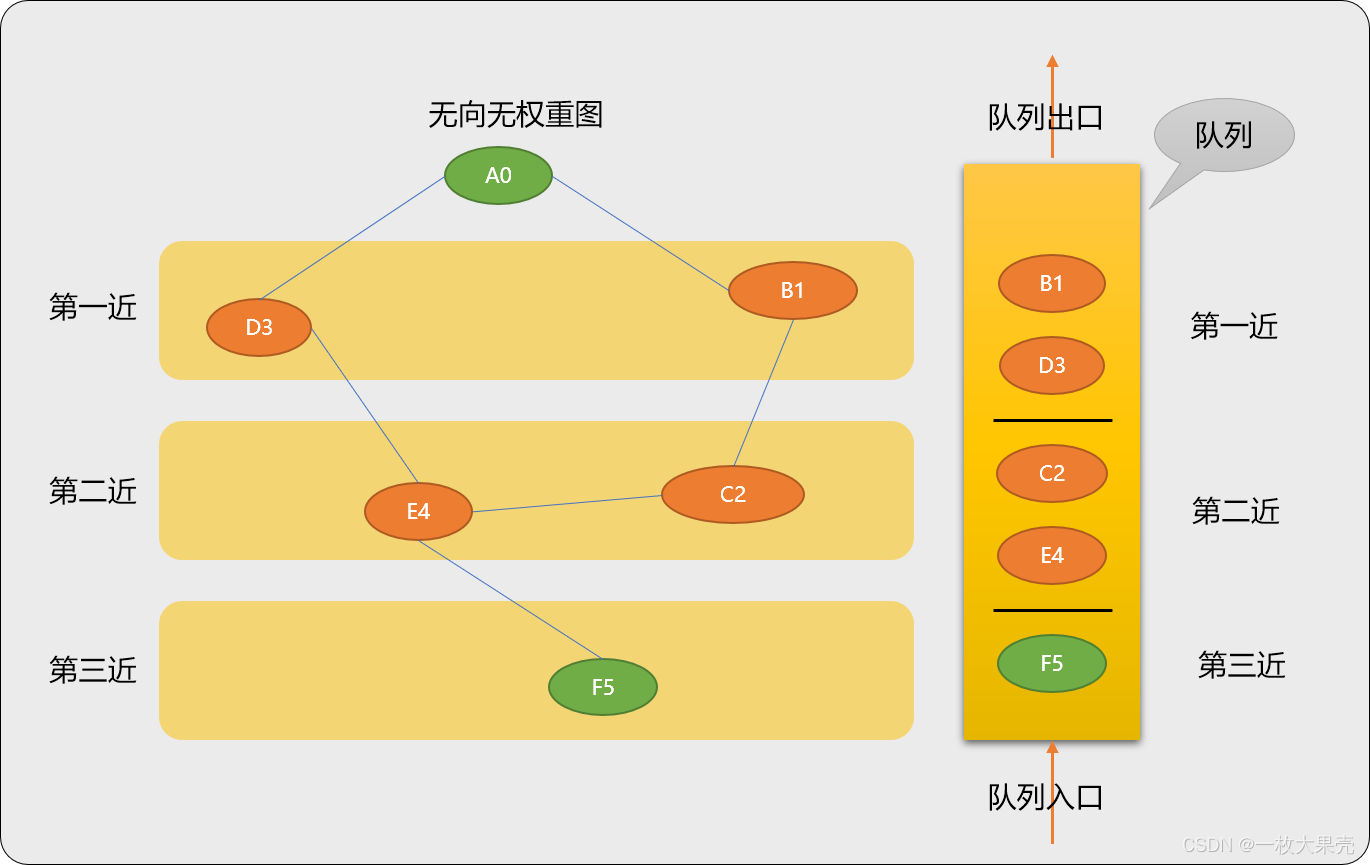
编码实现广度优先算法：

在顶点类中添加如下几个方法：

class Vertex:
    def __init__(self, v_name, v_id=0):
        # 顶点的编号
        self.v_id = v_id
        # 顶点的名称
        self.v_name = v_name
        # 是否被访问过:False 没有 True:有
        self.visited = False
        # 与此顶点相连接的其它顶点
        self.connected_to = {}

    '''
    添加邻接顶点
    nbr_ver:相邻顶点
    weight:无向无权重图，权重默认设置为 1
    '''
    def add_neighbor(self, nbr_ver, weight=1):
        # 以相邻顶点为键，权重为值
        self.connected_to[nbr_ver] = weight

    '''
    显示与当前顶点相邻的顶点
    '''
    def __str__(self):
        return '与 {0} 顶点相邻的顶点有:{1}'.format(self.v_name,
                                           str([(key.v_name, val) for key, val in self.connected_to.items()]))

    '''
    得到相邻顶点的权重
    '''
    def get_weight(self, nbr_v):
        return self.connected_to[nbr_v]

    '''
    判断给定的顶点是否和当前顶点相邻
    '''
    def is_neighbor(self, nbr_v):
        return nbr_v in self.connected_to

顶点类用来构造一个新顶点，并维护与相邻顶点的关系。

对图类中的方法做一下详细解释：

初始化方法：

class Graph:
    def __init__(self):
        # 一维列表，保存节点
        self.vert_list = {}
        # 顶点个数
        self.v_nums = 0
        # 使用队列模拟队列或栈，用于路径搜索算法
        self.queue_stack = []
        # 保存搜索到的路径
        self.searchPath = []

为图添加新顶点方法：

   def add_vertex(self, vert):
        if vert.v_name in self.vert_list:
            # 已经存在
            return
        # 顶点的编号内部生成
        vert.v_id = self.v_nums
        # 所有顶点保存在图所维护的字典中，以顶点名为键，顶点对象为值
        self.vert_list[vert.v_name] = vert
        # 数量增一
        self.v_nums += 1

顶点的编号由图对象内部指定，便于统一管理。

所有顶点保存在一个字典中，以顶点名称为键，顶点对象为值。也可以使用列表直接保存顶点，根据需要决定。

提供一个根据顶点名称返回顶点的方法：

 	'''
    根据顶点名找到顶点对象
    '''
    def find_vertex(self, v_name):
        if v_name in self.vert_list:
            return self.vert_list.get(v_name)
    # 查询所有顶点
    def find_vertexes(self):
        return [str(ver) for ver in self.vert_list.values()]

添加顶点与相邻顶点的关系：此方法属于一个封装方法，本质是调用顶点自身的添加相邻顶点方法。

    '''
    添加节点与节点之间的关系（边），
    如果是无权重图，统一设定为 1
    '''
    def add_edge(self, from_v, to_v, weight=1):
        # 如果节点不存在
        if from_v not in self.vert_list:
            self.add_vertex(from_v)
        if to_v not in self.vert_list:
            self.add_vertex(to_v)
        from_v.add_neighbor(to_v, weight)

图中核心方法：用来广度优先搜索算法查找顶点与顶点之间的路径

    '''
    广度优先搜索
    '''
    def bfs_nearest_path(self, from_v, to_v):
        tmp_path = []
        tmp_path.append(from_v)
        # 起始顶点不用压入队列
        from_v.visited = True
        # from_v 顶点的相邻顶点压入队列
        self.push_queue(from_v)
        while len(self.queue_stack) != 0:
            # 从队列中获取顶点
            v_ = self.queue_stack.pop(0)
            if from_v.is_neighbor(v_):
                # 如果 v_ 是 from_v 的后序相邻顶点，则连接成一条中路径信息
                tmp_path.append(v_)
                # 添加路径信息
                self.searchPath.append(tmp_path)
                tmp_path = tmp_path.copy()
                tmp_path.pop()
            else:
                for path_ in self.searchPath:
                    tmp_path = path_.copy()
                    tmp = tmp_path[len(tmp_path) - 1]
                    if tmp.is_neighbor(v_):
                        tmp_path.append(v_)
                        self.searchPath.append(tmp_path)
            if v_.v_id == to_v.v_id:
                break
            else:
                self.push_queue(v_)

    '''
     把某一顶点的相邻顶点压入队列
     '''
    def push_queue(self, vertex):
        # 获取 vertex 顶点的相邻顶点
        for v_ in vertex.connected_to.keys():
            # 检查此顶点是否压入过
            if v_.visited:
                continue
            vertex.visited = True
            self.queue_stack.append(v_)

广度优先搜索算法有一个核心点，当搜索到某一个顶点后，需要找到与此顶点相邻的其它顶点，并压入队列中。push_queue() 方法就是做些事情的。如果某一个顶点曾经进过队列，就不要再重复压入队列了。

测试代码：

'''
测试无向图最短路径
'''

if __name__ == '__main__':
    # 初始化图
    graph = Graph()
    # 添加节点
    for v_name in ['A', 'B', 'C', 'D', 'E', 'F']:
        v = Vertex(v_name)
        graph.add_vertex(v)

    # 添加顶点之间关系
    v_to_v = [('A', 'B'), ('A', 'D'), ('B', 'C'), ('C', 'E'), ('D', 'E'), ('E', 'F')]
    # 无向图中每 2 个相邻顶点之间互为关系
    for v in v_to_v:
        f_v = graph.find_vertex(v[0])
        t_v = graph.find_vertex(v[1])
        graph.add_edge(f_v, t_v)
        graph.add_edge(t_v, f_v)

    # 输出所有顶点
    print('-----------顶点及顶点之间的关系-------------')
    for v in graph.find_vertexes():
        print(v)

    # 查找路径
    print('-------------广度优先搜索--------------------')
    # 起始点
    f_v = graph.find_vertex('A')
    # 目标点
    t_v = graph.find_vertex('F')
    # 广度优先搜索
    graph.bfs_nearest_path(f_v, t_v)
    for path in graph.searchPath:
        weight = 0
        for idx in range(len(path)):
            if idx != len(path) - 1:
                weight += path[idx].get_weight(path[idx + 1])
            print(path[idx].v_name, end='-')
        print("的最短路径长度，", weight)

输出结果：

-----------顶点及顶点之间的关系-------------
与 A 顶点相邻的顶点有:[('B', 1), ('D', 1)]
与 B 顶点相邻的顶点有:[('A', 1), ('C', 1)]
与 C 顶点相邻的顶点有:[('B', 1), ('E', 1)]
与 D 顶点相邻的顶点有:[('A', 1), ('E', 1)]
与 E 顶点相邻的顶点有:[('C', 1), ('D', 1), ('F', 1)]
与 F 顶点相邻的顶点有:[('E', 1)]
-------------广度优先搜索--------------------
A-B-的最短路径长度， 1
A-D-的最短路径长度， 1
A-B-C-的最短路径长度， 2
A-D-E-的最短路径长度， 2
A-B-C-E-的最短路径长度， 3
A-D-E-的最短路径长度， 2
A-B-C-E-的最短路径长度， 3
A-D-E-F-的最短路径长度， 3
A-B-C-E-F-的最短路径长度， 4
A-D-E-F-的最短路径长度， 3
A-B-C-E-F-的最短路径长度， 4

广度优先搜索算法也可以使用递归方案：

    '''
    递归实现
    '''

    def bfs_nearest_path_dg(self, from_v, to_v):

        # 相邻顶点
        self.push_queue(from_v)
        tmp_v = self.queue_stack.pop(0)
        if not tmp_v.visited:
            self.searchPath.append(tmp_v)
        if tmp_v.v_id == to_v.v_id:
            return

        self.bfs_nearest_path_dg(tmp_v, to_v)

在无向图中，查找起始点到目标点的最短路径，使用广度优先搜索算法便可实现，但如果是有向加权图，可能不会称心如愿。因有向加权图中的边是有权重的。所以对于有向加权图则需要另择方案。

3. 总结

图数据结构的实现过程中会涉及到其它数据结构的运用。学习、使用图数据结构对其它数据结构有重新认识和巩固作用。