NOIp 2014 #3 寻找道路 Label:图论

题目描述

在有向图G 中，每条边的长度均为1 ，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1 ．路径上的所有点的出边所指向的点都直接或间接与终点连通。

2 ．在满足条件1 的情况下使路径最短。

注意：图G 中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

输入输出格式

输入格式：

输入文件名为road .in。

第一行有两个用一个空格隔开的整数n 和m ，表示图有n 个点和m 条边。

接下来的m 行每行2 个整数x 、y ，之间用一个空格隔开，表示有一条边从点x 指向点y 。

最后一行有两个用一个空格隔开的整数s 、t ，表示起点为s ，终点为t 。

输出格式：

输出文件名为road .out 。

输出只有一行，包含一个整数，表示满足题目᧿述的最短路径的长度。如果这样的路径不存在，输出- 1 。

输入输出样例

输入样例#1：

3 2
1 2
2 1
1 3

输出样例#1：

-1

输入样例#2：

6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5

输出样例#2：

3

说明

解释1：

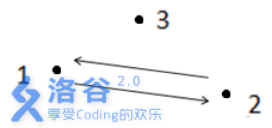
如上图所示，箭头表示有向道路，圆点表示城市。起点1 与终点3 不连通，所以满足题

目᧿述的路径不存在，故输出- 1 。

解释2：

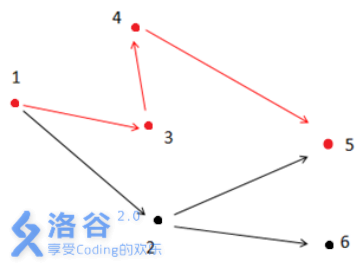
如上图所示，满足条件的路径为1 - >3- >4- >5。注意点2 不能在答案路径中，因为点2连了一条边到点6 ，而点6 不与终点5 连通。

对于30%的数据，0<n≤10，0<m≤20；

对于60%的数据，0<n≤100，0<m≤2000；

对于100%的数据，0<n≤10,000，0<m≤200,000，0<x，y，s，t≤n，x≠t。

代码

 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<queue>
 #define MAXN 500005
 #define INF 0x3f3f3f3f
 using namespace std;

 int vis[MAXN],to_des[MAXN],dis[MAXN];
 int N,M;
 int s,t;

 struct cc{int d,num;};
 struct cmp{bool operator()(cc a,cc b){return a.d>b.d;}};
 cc make_(int d,int num){cc a;a.d=d;a.num=num;return a;}

 vector<int> rG[MAXN],G[MAXN];

 void Dijkstra(){
     priority_queue<cc,vector<cc>,cmp> q;
     memset(dis,0x3f,sizeof(dis));
     memset(vis,,sizeof(vis));

     q.push(make_(,s));
     dis[s]=;

     while(!q.empty()){
         cc x=q.top();q.pop();
         vis[x.num]=;

         int flag=;
         for(int i=;i<G[x.num].size();i++){
             int to=G[x.num][i];
             if(!to_des[to]) {flag=;break;}
         }
         if(flag) continue;

         for(int i=;i<G[x.num].size();i++){
             int to=G[x.num][i];
             if(dis[x.num]+<dis[to]){
                 dis[to]=dis[x.num]+;
                 q.push(make_(dis[to],to));
             }
         }
     }
 }

 void rdfs(int x){
     vis[x]=to_des[x]=;
     for(int i=;i<rG[x].size();i++){
         int to=rG[x][i];
         if(!vis[to]) rdfs(to);
     }
 }

 void init_(){
     scanf("%d%d",&N,&M);
     for(int i=;i<=M;i++){
         int from,to;
         scanf("%d%d",&from,&to);
         G[from].push_back(to);
         rG[to].push_back(from);
     }
     scanf("%d%d",&s,&t);
     rdfs(t);
 }

 int main(){
     freopen("road.in","r",stdin);
     freopen("road.out","w",stdout);

     init_();
     Dijkstra();

     if(dis[t]==INF) puts("-1");
     else printf("%d\n",dis[t]);

     return ;
 }

90分 TLE

转载：

首先把路线全倒过来，从终点往起点走一遍，把不行的点标起来，然后再从起点往终点做一个bfs，求最短的路线，就行了

 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 #include<iostream>
 #include<vector>
 using namespace std;
 int x,y,s,t,n,m,h[],f[],tr;
 vector<int>a[],b[];
 void dfs(int u){
     if (h[u])return;
     f[u]=;h[u]=;
     for (int i=;i<b[u].size();i++)
     dfs(b[u][i]);
 }
 void bfs(int u){
     int g[],ans[],l=,fl[],xx;
     memset(fl,,sizeof(fl));memset(ans,,sizeof(ans));
     for (int i=;i<a[u].size();i++)
     if (!fl[a[u][i]] && f[a[u][i]])
     {ans[l]=;g[l++]=a[u][i];fl[a[u][i]]=;}
     for (int i=;i<l;i++)
     {
         if (g[i]==t){tr=;printf("%d",ans[i]);break;}
         xx=g[i];
         for (int j=;j<a[xx].size();j++)
         if (!fl[a[xx][j]] && f[a[xx][j]])
         {ans[l]=ans[i]+;g[l++]=a[xx][j];fl[a[xx][j]]=;}
     }
 }
 int main()
 {
     scanf("%d%d",&n,&m);
     for (int i=;i<m;i++)
     {
         scanf("%d%d",&x,&y);
         a[x].push_back(y);b[y].push_back(x);
     }
     scanf("%d%d",&s,&t);
     dfs(t);
     memset(h,,sizeof(h));
     for (int i=;i<=n;i++)
     {
         if (!f[i])continue;
         for (int j=;j<a[i].size();j++)
         if (!f[a[i][j]]){h[i]=;break;}
     }
     for (int i=;i<=n;i++)
     if (h[i])f[i]=;
     if (f[s])bfs(s);
     if (!tr)printf("-1");
     return ;
 }

std