纸上谈兵：AVL树

作者：Vamei 出处：http://www.cnblogs.com/vamei 欢迎转载，也请保留这段声明。谢谢！

二叉搜索树的深度与搜索效率

我们在树, 二叉树, 二叉搜索树中提到，一个有n个节点的二叉树，它的最小深度为log(n)，最大深度为n。比如下面两个二叉树:

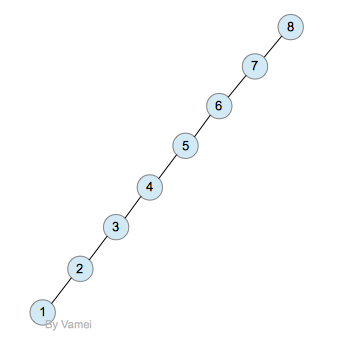
深度为n的二叉树

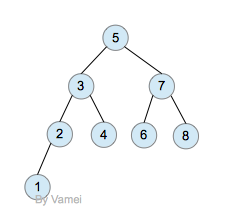
深度为log(n)的二叉树

这两个二叉树同时也是二叉搜索树(参考树, 二叉树, 二叉搜索树)。注意，log以2为基底。log(n)是指深度的量级。根据我们对深度的定义，精确的最小深度为floor(log(n)+1)。

我们将处于同一深度的节点归为一层。如果除最后一层外的其他层都被节点填满时，二叉树有最小深度log(n)。

二叉搜索树的深度越小，那么搜索所需要的运算时间越小。一个深度为log(n)的二叉搜索树，搜索算法的时间复杂度也是log(n)。然而，我们在二叉搜索树中已经实现的插入和删除操作并不能让保持log(n)的深度。如果我们按照8，7，6，5，4，3，2，1的顺序插入节点，那么就是一个深度为n的二叉树。那么，搜索算法的时间复杂度为n。

n和log(n)的时间复杂度意味着什么呢？时间复杂度代表了完成算法所需要的运算次数。时间复杂度越小，算法的速度越快。

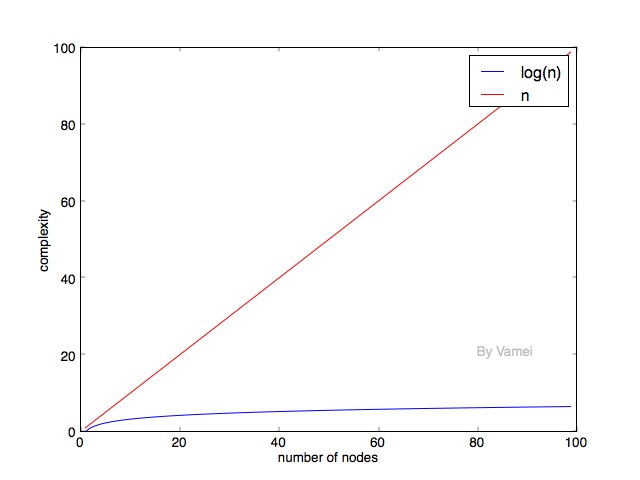
可以看到，随着元素的增加，log(n)的时间复杂度的增长要远小于n。所以，我们自然希望二叉搜索树能尽可能保持log(n)的深度。在上面深度为n的例子中，我们发现，每个节点只有左节点被填满。树的每一层都有很多空位。能不能尽可能减少每一层的空位呢？ (相应的，减少树的深度)

“紧致”的树

一种想法是先填满一层，再去填充下一层，这样就是一个完全二叉树(complete binary tree)。这样的二叉树实现插入算法会比较复杂。我们将介绍一种思路相似，但比较容易实现的树状数据结构——AVL树。

AVL树

AVL树是根据它的发明者G. M. Adelson-Velskii和E. M. Landis命名的。它是一种特殊的二叉搜索树。AVL树要求: 任一节点的左子树深度和右子树深度相差不超过1

(空树的深度为0。注意，有的教材中，采用了不同的深度定义方法，所以空树的深度为-1)

下面是AVL树:

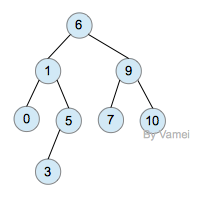
AVL树

AVL树的特性让二叉搜索树的节点实现平衡(balance)：节点相对均匀分布，而不是偏向某一侧。因此，AVL树的搜索算法复杂度是log(n)的量级。

我们在二叉搜索树中定义的操作，除了插入，都可以用在AVL树上 (假设使用懒惰删除)。如果进行插入操作，有可能会破坏AVL树的性质，比如:

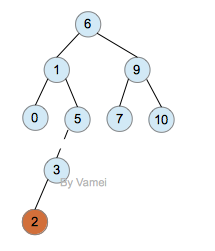
插入2: 破坏AVL树

观察节点5，它的左子树深度为2，右子树深度为0，所以左右两个子树深度相差为2，不再是AVL树。由于2的加入，从节点6，1，5，3到2的层数都增加1。6, 1, 5节点的AVL性质都被破坏。如果从节点2向上回溯，节点5是第一个被破坏的。从节点3开始的子树深度加1，这是造成6, 1, 5的AVL性质被破坏的本质原因。我们将5和3之间的路径画成虚线(就好像挂了重物，边被拉断一样)。

我们可以通过单旋照(single rotation)，调整以5为根节点的子树，来修正因为插入一个元素而引起的对AVL性质的破坏。如下:

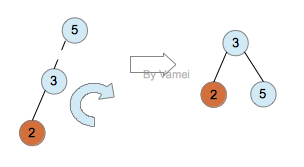
Single rotation: 左侧超重，向右转

通过单旋转，3成为新的根节点，2,5称为3的左右子节点。子树重新成为AVL树。该子树的深度减小1，这将自动修正2带给节点6,1的“超负荷”。

单旋转效果如下：

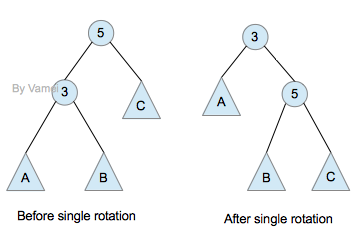 向右单旋转

特别要注意的是，为了保持二叉树的性质，子树B过继给了节点5。

向左单旋转与之类似。作为练习，可以尝试绘制向左单旋转的示意图。

但如果插入的节点不是2，而是4，会是如何呢？

插入4

尝试单旋转，会发现无法解决问题。以5为根节点的子树向右单旋转后，树将以3为根节点，4,5为子节点。4比3大，却是3的左子节点，显然，这依然不符合二叉搜索树的性质。但基于和上面相似的原则(调整以5为根节点的树)，我们发现有一个简单的解决方式：

double rotation

上面的操作被称作双旋转(double rotation)。双旋转实际上是进行两次单旋转: 4为根节点的子树先进行一次向左的单旋转，然后将5为根节点的子树进行了一次向右的单旋转。这样恢复了树的ACL性质。

对于AVL树，可以证明，在新增一个节点时，总可以通过一次旋转恢复AVL树的性质。

当我们插入一个新的节点时，在哪里旋转？是用单旋转还是双旋转?

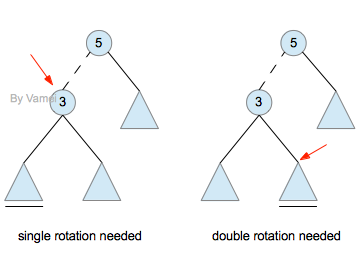
我们按照如下基本步骤进行：

1. 按照二叉搜索树的方式增加节点，新增节点称为一个叶节点。

2. 从新增节点开始，回溯到第一个失衡节点(5)。

(如果回溯到根节点，还没有失衡节点，就说明该树已经符合AVL性质。)

3. 找到断的边(5->3)，并确定断弦的方向(5的左侧)

4. 以断边下端(3)为根节点，确定两个子树中的哪一个深度大(左子树还是右子树)。

(这两棵子树的深度不可能相等，而且深度大的子树包含有新增节点。想想为什么)

5. 如果第2和第3步中的方向一致(都为左或者都为右)，需要单旋转以失衡节点为根节点的子树。

否则，双旋转以失衡节点为根节点的子树。

下面是AVL树的插入算法实现如下:

/* By Vamei */
/* binary search tree */
#include <stdio.h>
#include <stdlib.h>

typedef struct node *position;
typedef int ElementTP;

struct node {
    int depth;
    position parent;
    ElementTP element;
    position lchild;
    position rchild;
};

/* pointer => root node of the tree */
typedef struct node *TREE;

position insert_value(TREE, ElementTP);
int depth(TREE);

static void insert_node_to_nonempty_tree(TREE, position);
static void update_root_depth(TREE);
static TREE recover_avl(TREE, position);
static int depth_diff(TREE);
static position insert_leaf(TREE, ElementTP);
static void insert_node_to_nonempty_tree(TREE, position);
static TREE left_single_rotate(TREE);
static TREE left_double_rotate(TREE);
static TREE right_single_rotate(TREE);
static TREE right_double_rotate(TREE);

void main(void)
{
    TREE tr;
    position np;
    ElementTP element;
    tr = NULL;
    tr = insert_value(tr, 18);
    tr = insert_value(tr, 5);
    printf("root: %d\n", tr->element);
    printf("depth: %d\n", depth(tr));
    tr = insert_value(tr, 2);
    printf("root: %d\n", tr->element);
    printf("depth: %d\n", depth(tr));
    tr = insert_value(tr, 4);
    printf("root: %d\n", tr->element);
    printf("depth: %d\n", depth(tr));
    printf("root->lchild: %d\n", tr->lchild->element);
    tr = insert_value(tr, 3);
    printf("root: %d\n", tr->element);
    printf("depth: %d\n", depth(tr));
    printf("root->lchild: %d\n", tr->lchild->element);
    printf("root->lchild->lchild: %d\n", tr->lchild->lchild->element);
}

/*
 * insert value
 *
 */
position insert_value(TREE tr, ElementTP value)
{
    position new;

    /* insert a value to a binary search tree */
    new = insert_leaf(tr, value);
    update_root_depth(new);
    if (tr == NULL) {
        tr = new;
    }
    else {
        tr = recover_avl(tr, new);
    }
    return tr;
}

/*
 * get the depth of the tree
 * use this function to access depth
 */
int depth(TREE tr) {
    if (tr == NULL) {
        return 0;
    }
    else {
        return tr->depth;
    }
}

//========================================
// static functions: for internal use

/*
 * traverse the path from new node to root node
 * make one rotation, recover AVL and stop
 */
static TREE recover_avl(TREE tr, position np)
{
    int myDiff;
    while (np != NULL) {
        update_root_depth(np);
        myDiff = depth_diff(np);
    if (myDiff > 1 || myDiff < -1) {
            if (myDiff > 1) {
                /* left rotate needed */
                if(depth_diff(np->rchild) > 0) {
                    np = left_single_rotate(np);
                }
                else {
                    np = left_double_rotate(np);
                }
            }
            if (myDiff < -1) {
                if(depth_diff(np->lchild) < 0) {
                    np = right_single_rotate(np);
                }
                else {
                    np = right_double_rotate(np);
                }
            }
            /* if rotation changes root node */
            if (np->parent == NULL) tr = np;
            break;
        }
        np = np->parent;
    }

    return tr;
}

/*
 * difference of rchild->depth and lchild->depth
 */
static int depth_diff(TREE tr)
{
    if (tr == NULL) {
        return 0;
    }
    else {
        return depth(tr->rchild) - depth(tr->lchild);
    }
}

/*
 * left single rotation
 * return the new root
 */
static TREE left_single_rotate(TREE tr)
{
    TREE newRoot, parent;
    parent  = tr->parent;
    newRoot = tr->rchild;
    /* detach & attach */
    if (newRoot->lchild != NULL) newRoot->lchild->parent = tr;
    tr->rchild = newRoot->lchild;
    update_root_depth(tr);

    /* raise new root node */
    newRoot->lchild = tr;
    newRoot->parent = parent;
    if (parent != NULL) {
        if (parent->lchild == tr) {
        parent->lchild = newRoot;
    }
    else {
        parent->rchild = newRoot;
    }
    }
    tr->parent = newRoot;
    update_root_depth(newRoot);
    return newRoot;
}

/*
 * right single rotation
 * return the new root
 */
static TREE right_single_rotate(TREE tr)
{
    TREE newRoot, parent;
    parent  = tr->parent;
    newRoot = tr->lchild;

    /* detach & attach */
    if (newRoot->rchild != NULL) newRoot->rchild->parent = tr;
    tr->lchild = newRoot->rchild;
    update_root_depth(tr);

    /* raise new root node */
    newRoot->rchild = tr;
    newRoot->parent = parent;
    if (parent != NULL) {
        if (parent->lchild == tr) {
        parent->lchild = newRoot;
    }
    else {
        parent->rchild = newRoot;
    }
    }
    tr->parent = newRoot;
    update_root_depth(newRoot);
    return newRoot;
}

/*
 * left double rotation
 * return
 */
static TREE left_double_rotate(TREE tr)
{
    right_single_rotate(tr->rchild);
    return left_single_rotate(tr);
}

/*
 * right double rotation
 * return
 */
static TREE right_double_rotate(TREE tr)
{
    left_single_rotate(tr->lchild);
    return right_single_rotate(tr);
}

/*
 * update tr->depth
 * assume lchild->depth and rchild->depth are correct
 */
static void update_root_depth(TREE tr)
{
    int maxChildDepth;
    int depLChild, depRChild;
    if (tr==NULL) return;
    else {
        depLChild = depth(tr->lchild);
        depRChild = depth(tr->rchild);
        maxChildDepth = depLChild > depRChild ? depLChild : depRChild;
        tr->depth = maxChildDepth + 1;
    }
}

/*
 * insert a new value into the tree as a leaf
 * return address of the new node
 */
static position insert_leaf(TREE tr, ElementTP value)
{
    position np;
    /* prepare the node */
    np = (position) malloc(sizeof(struct node));
    np->element = value;
    np->parent  = NULL;
    np->lchild  = NULL;
    np->rchild  = NULL;

    if (tr != NULL) {
        insert_node_to_nonempty_tree(tr, np);
    }
    return np;
}

/*
 * insert a node to a non-empty tree
 * called by insert_value()
 */
static void insert_node_to_nonempty_tree(TREE tr, position np)
{
    /* insert the node */
    if(np->element <= tr->element) {
        if (tr->lchild == NULL) {
            /* then tr->lchild is the proper place */
            tr->lchild = np;
            np->parent = tr;
            return;
        }
        else {
            insert_node_to_nonempty_tree(tr->lchild, np);
        }
    }
    else if(np->element > tr->element) {
        if (tr->rchild == NULL) {
            tr->rchild = np;
            np->parent = tr;
            return;
        }
        else {
            insert_node_to_nonempty_tree(tr->rchild, np);
        }
    }
}

输出如下：

root: 18
depth: 2

root: 5
depth: 2

root: 5
depth: 3
root->lchild: 2

depth: 3
root->lchild: 3
root->lchild->lchild: 2

(空行是额外加的)

总结:

AVL树: 平衡，深度相差不超过1

单旋转，双旋转