Chap4: question: 19 - 28

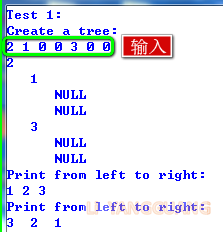
19. 二叉树的镜像（递归）

即：交换所有节点的左右子树。从下往上 或 从上往下 都可以。

#include <iostream>
#include <string>
using namespace std;
struct BTNode
{
	int v;  // default positive Integer.
	BTNode *pLeft;
	BTNode *pRight;
	BTNode(int x) : v(x), pLeft(NULL), pRight(NULL) {}
};
/********************************************************/
/*****        Basic functions          ***********/
BTNode* createBinaryTree(int r)
{
	BTNode *pRoot = new BTNode(r);
	int u, v;
	cin >> u >> v;
	if(u != 0)
		pRoot->pLeft = createBinaryTree(u);
	if(v != 0)
		pRoot->pRight = createBinaryTree(v);
	return pRoot;
}
void release(BTNode *root){
	if(root == NULL) return;
	release(root->pLeft);
	release(root->pRight);
	delete[] root;
	root = NULL;
}
void print(BTNode *root, int level = 1){
	if(root == NULL) { cout << "NULL"; return; };
	string s;
	for(int i = 0; i < level; ++i) s += "   ";
	cout << root->v << endl << s;
	print(root->pLeft, level+1);
	cout << endl << s;
	print(root->pRight, level+1);
}
/******************************************************************/
void mirrorTree(BTNode *root)
{
	if(!root || (!root->pLeft && !root->pRight)) return;
	/*    交换左右子树           */
	BTNode *pTem = root->pLeft;
	root->pLeft = root->pRight;
	root->pRight = pTem;
 
	mirrorTree(root->pLeft);
	mirrorTree(root->pRight);
}
 
int main(){
	int TestTime = 3, k = 1;
	while(k <= TestTime)
	{
		cout << "Test " << k++ << ":" << endl;
 
		cout << "Create a tree: " << endl;
		BTNode *pRoot = createBinaryTree(8);
		print(pRoot);
		cout << endl;
 
		cout << "The mirror tree: " << endl;
		mirrorTree(pRoot);
		print(pRoot);
		cout << endl;
 
		release(pRoot);
	}
	return 0;
}

 20. 顺时针打印矩阵

 #include <stdio.h>
 
 void printMatrix(int (*A)[], int rows, int columns)
 {
     if(rows <  || columns < ) return;
     int r1, r2, c1, c2;
     r1 = c1 = , r2 = rows-, c2 = columns-;
     while(r1 <= r2 && c1 <= c2) /* 打印结束时， r1 = r2+1, c1 = c2+1; */
     {
         for(int i = c1; i <= c2 && r1 <= r2; ++i)
             printf("%d ", A[r1][i]);
         ++r1;
         for(int i = r1; c1 <= c2 && i <= r2; ++i)
             printf("%d ", A[i][c2]);      /*   要保证 c1 <= c2  */
         --c2;
         for(int i = c2; i >= c1 && r1 <= r2; --i)
             printf("%d ", A[r2][i]);
         --r2;
         for(int i = r2; i >= r1 && c1 <= c2; --i)
             printf("%d ", A[i][c1]);
         ++c1;
     }
     printf("\n");
 }
 int main()
 {
     int test1[][] = {{, , },
                        {, , },
                         {, , }};
     printMatrix(test1, , );
 
     int test2[][] = {, , };
     printMatrix(test2, , );
 
 /*  // first set int (*A)[1], then began called below.
     int test3[3][1] = {{1}, {2}, {3}};
     printMatrix(test3, 3, 1);
 
     int test4[1][1] = {1};
     printMatrix(test4, 1, 1);
 */
     return ;
 }

     （）

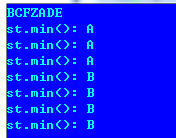
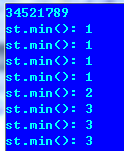
21. 包含 min  函数的栈

 要求调用 min，pop，push，时间复杂度都是 O(1)。

 #include <iostream>
 #include <stack>
 #include <cassert>
 #include <string>
 template<typename T> class Stack
 {
 public:
     void push(T value);
     void pop();
     T min();
 private:
     std::stack<T> data;
     std::stack<T> minData;
 };
 template<typename T> void Stack<T>::push(T value)
 {
     data.push(value);
     if(minData.empty() || minData.top() >= value)
         minData.push(value);
     else
         minData.push(minData.top());
 }
 template<typename T> void Stack<T>::pop()
 {
     assert(data.size() >  && minData.size() > );
     data.pop();
     minData.pop();
 }
 template<typename T> T Stack<T>::min()
 {
     return minData.top();
 }
 
 int main()
 {
     Stack<char> st;
     std::string numbers;
     while(std::cin >> numbers)
     {
         for(size_t i = ; i < numbers.length(); ++i) st.push(numbers[i]);
         for(size_t i = ; i < numbers.length(); ++i)
         {
             std::cout << "st.min(): " << st.min() << std::endl;
             st.pop();
         }
     }
     return ;
 }

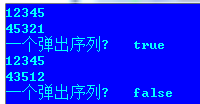
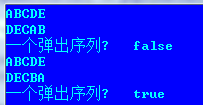
22. 根据栈的压入序列，判断一个序列是否是弹出序列。 

#include <iostream>
#include <string>
 
bool isPopOrder(const std::string pushS, const std::string popS)
{
	size_t outId1 = 0, outId2 = 0, len1 = pushS.length(), len2 = popS.length();
	if(len1 != len2) return false;
	int *stack = new int[len1];
	int tail = 0; // 栈尾
	while(outId1 < len1 && outId2 < len2)
	{
		while(pushS[outId1] != popS[outId2])
		{
			stack[tail++] = pushS[outId1++]; // 入栈
		}
		outId1++, outId2++;
		while(tail != 0 && popS[outId2] == stack[tail-1])
		{
			++outId2;
			tail--;     // 出栈
		}
	}
	delete[] stack;
	if(tail == 0) return true; // 栈空
	else return false;
}
 
int main()
{
	std::string numbers;
	std::string popNumbers;
	while(std::cin >> numbers >> popNumbers)
	{
		std::cout << "一个弹出序列?   " ;
 
		if(isPopOrder(numbers, popNumbers))
			std::cout << "true" << std::endl;
		else std::cout << "false" << std::endl;
	}
	return 0;
}

23. 从上往下打印二叉树

 Go:（Chap2: question: 1 - 10—>6. 重建二叉树—>二叉树的各种遍历）Link: http://www.cnblogs.com/liyangguang1988/p/3667443.html

24. 判断序列是否为二叉搜索树的后序遍历（递归）

note: 二叉搜索树和遍历序列一一对应。

例：后序序列 {3，5，4，6，11，13，12, 10, 8} ，可画出一颗二叉搜索树。

 #include <iostream>
 /* verify the seq which should be the postOrder of a Binary Search Tree  */
 bool postOrderOfBST(int sequence[], int len)
 {
     if(sequence == NULL || len == ) return false;
     bool answer = false;
     int root = sequence[len-];    /* value of root node */
 
     int leftLength = ;
     for(; leftLength < len-; ++leftLength)
     {
         if(sequence[leftLength] > root) break;
     }
     /*  verify right-subtree, should big than root  */
     for(int i = leftLength + ; i < len -; ++i)
     {
         if(sequence[i] < root) return false;
     }
 
     int rightLength = len -  - leftLength;
     bool left = true, right = true;
     if(leftLength > )
         bool left = postOrderOfBST(sequence, leftLength);
     if(rightLength)
         bool right = postOrderOfBST(sequence+leftLength, rightLength);
     return (left && right);
 }
 
 void printResult(bool v)
 {
     std::cout << "Is LRD of a BFS?  " ;
     if(v)  std::cout << "true" << std::endl;
     else  std::cout << "false" << std::endl;
 }
 int main()
 {
     std::cout << "Test 1: ";
     int test1[] = {, , , , , , , , };
     printResult(postOrderOfBST(test1, sizeof(test1) / )) ;
 
     std::cout << "Test 2: ";
     int test2[] = {, , };
     printResult(postOrderOfBST(test2, sizeof(test2) / )); 
 
     std::cout << "Test 3: ";
     int test3[] = {};
     printResult(postOrderOfBST(test3, sizeof(test3) / ));
 
     return ;
 } 

 25. 二叉树中和为某一值的路径（递归）

 #include <iostream>
 #include <string>
 #include <vector>
 using namespace std;
 struct BTNode
 {
     int v;  // default positive Integer.
     BTNode *pLeft;
     BTNode *pRight;
     BTNode(int x) : v(x), pLeft(NULL), pRight(NULL) {}
 };
 /********************************************************/
 /*****        Basic functions          ***********/
 BTNode* createBinaryTree(int r)
 {
     BTNode *pRoot = new BTNode(r);
     int u, v;
     cin >> u >> v;
     if(u != )
         pRoot->pLeft = createBinaryTree(u);
     if(v != )
         pRoot->pRight = createBinaryTree(v);
     return pRoot;
 }
 void release(BTNode *root){
     if(root == NULL) return;
     release(root->pLeft);
     release(root->pRight);
     delete[] root;
     root = NULL;
 }
 void print(BTNode *root, int level = ){
     if(root == NULL) { cout << "NULL"; return; };
     string s;
     for(int i = ; i < level; ++i) s += "\t";
     cout << root->v << endl << s;
     print(root->pLeft, level+);
     cout << endl << s;
     print(root->pRight, level+);
 }
 /******************************************************************/
 void findPath(BTNode *root, int target, vector<int>& path, int curSum)
 {
     if(root == NULL) return;
     curSum += root->v;
     path.push_back(root->v);
     if(!root->pLeft && !root->pRight && (curSum == target))  // root node is a leaf, get a path.
     {
         for(auto it = path.begin(); it != path.end(); ++it)
             cout << *it << " ";
         cout << endl;
     }
     findPath(root->pLeft, target, path, curSum);
     findPath(root->pRight, target, path, curSum);
     path.pop_back();
 }
 
 void findPath(BTNode *root, int target)
 {
     if(root == NULL) return;
     vector<int> path;
     findPath(root, target, path, );
 }
 
 int main(){
     int TestTime = , k = ;
     while(k <= TestTime)
     {
         int root;
         cout << "Test " << k++ << ":" << endl; 
 
         cout << "Create a tree: " << endl;
         cin >> root;
         BTNode *pRoot = createBinaryTree(root);
         print(pRoot);
         cout << endl; 
 
         cout << "target :  22" << endl << "findPath :" << endl;
         findPath(pRoot, );
 
         release(pRoot);
     }
     return ;
 } 

Code

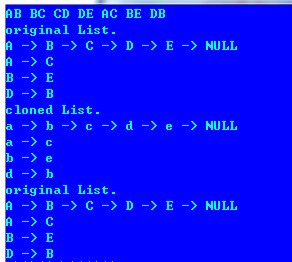
 26. 复杂链表的复制

 #include <stdio.h>
 typedef char Elem;
 typedef struct ComplexListNode
 {
     Elem e;
     ComplexListNode *next;
     ComplexListNode *sibling;
 } ComplexList;
 ComplexListNode Node[] = {};
 /***************************************************************/
 ComplexList* creatComplexList()
 {
     for(int i = ; i < ; ++i)
         Node[i].e = i + 'A';
     char u, v;
     while((scanf("%c%c", &u, &v) == ) )
     {
         if(u >= 'A' && u <= 'Z' && v >= 'A' && v <= 'Z')
         {
             if(Node[u-'A'].next == NULL)
                 Node[u-'A'].next = &Node[v-'A'];
             else if(Node[u-'A'].sibling == NULL)
                 Node[u-'A'].sibling = &Node[v-'A'];
         }
         if(getchar() == '\n') break;
     }
     return &Node[];
 }
 
 void printComplexList(ComplexList *pHead)
 {
     ComplexListNode *p = pHead;
     while(p != NULL)
     {
         printf("%c -> ", p->e);
         p = p->next;
     }
     printf("NULL\n");
     p = pHead;
     while(p != NULL)
     {
         if(p->sibling != NULL)
         {
             printf("%c -> ", p->e);
             printf("%c\t", p->sibling->e);
         }
         p = p->next;
     }
 }
 /***************************************************************************/
 void cloneNodes(ComplexList *pHead)
 {
     ComplexListNode *p = pHead;
     while(p != NULL)
     {
         ComplexListNode *newNode = new ComplexListNode;
         newNode->e = p->e + ;
         newNode->next = p->next;
         newNode->sibling = NULL;
         p->next = newNode;
         p = newNode->next;
     }
 }
 
 void connectSibling(ComplexList *pHead)
 {
     ComplexListNode *pPre = pHead, *p;
     while(pPre != NULL && pPre->next != NULL)
     {
         p = pPre->next;
         if(pPre->sibling != NULL)
             p->sibling = pPre->sibling->next;
         pPre = p->next;
     }
 }
 
 ComplexList* getClonedComplexList(ComplexList *pHead)
 {
     ComplexListNode *pPre = pHead, *newHead = NULL, *p;
     while(pPre != NULL && pPre->next != NULL)
     {
         if(newHead != NULL)
         {
             p->next = pPre->next;
             p = p->next;
         }
         else
         {
             newHead = pPre->next;
             p = newHead;
         }
         pPre->next = pPre->next->next;
         pPre = pPre->next;
     }
     return newHead;
 }
 
 ComplexList* clone(ComplexList *pHead)
 {
     cloneNodes(pHead);
     connectSibling(pHead);
     return getClonedComplexList(pHead);
 }
 
 int main()
 {
     ComplexList *pHead = creatComplexList();
     printf("original List.\n");
     printComplexList(pHead);
 
     ComplexList *newHead = clone(pHead);
     printf("cloned List.\n");
     printComplexList(newHead);
 
     printf("original List.\n");
     printComplexList(pHead);
 
     return ;
 }

程序说明：对一个结点，若 next 和 sibling 同时为 0，先保存 next 指针。
样例输入：AB AC BC BE CD DE DB(回车换行)

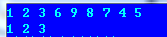
 27.二叉搜索树生成有序双向链表

 #include <iostream>
 #include <string>
 using namespace std;
 typedef struct BTNode
 {
     int v;     // In this code, default positive Integer.
     BTNode *pLeft;
     BTNode *pRight;
     BTNode(int x) : v(x), pLeft(NULL), pRight(NULL) {}
 } DbList;
 /********************************************************/
 /*****        Basic functions  for binary tree     ***********/
 BTNode* createBinaryTree() // input a preOrder sequence, 0 denote empty node.
 {
     BTNode *pRoot = NULL;
     int r;
     cin >> r;
     if(r != )         // equal to if(!r) return;
     {
         pRoot = new BTNode(r);
         pRoot->pLeft = createBinaryTree();
         pRoot->pRight = createBinaryTree();
 
     }
     return pRoot;
 } 
 
 void printBinaryTree(BTNode *root, int level = ){
     if(root == NULL) { cout << "NULL"; return; };
     string s;
     for(int i = ; i < level; ++i) s += "   ";
     cout << root->v << endl << s;
     printBinaryTree(root->pLeft, level+);
     cout << endl << s;
     printBinaryTree(root->pRight, level+);
 } 
 
 // void releaseBinaryTree(BTNode *root){
 //     if(root == NULL) return;
 //     releaseBinaryTree(root->pLeft);
 //     releaseBinaryTree(root->pRight);
 //     delete[] root;
 //     root = NULL;
 // }
 /******************************************************************/
 /****************** basic function for double linked list. *******/
 void printDbList(DbList *pHead)
 {
     if(pHead == NULL) return;
     DbList *p = pHead;
     cout << "Print from left to right:" << endl;
     while(p->pRight != NULL) { cout << p->v << " "; p = p->pRight;}
     cout << p->v << endl;
 
     cout << "Print from left to right:" << endl;
     while(p != NULL) { printf("%-3d", p->v); p = p->pLeft;}
     cout << endl;
 }
 void releaseDbList(DbList *pHead)
 {
     if(pHead == NULL) return;
     releaseDbList(pHead->pRight);
     delete[] pHead;
 }
 /******************************************************************/
 /*****   binary search tree translate to double linked list    ******/
 void convert(BTNode *root, BTNode **tail)
 {
     if(root == NULL) return;
 
     if(root->pLeft != NULL)
         convert(root->pLeft, tail);
     root->pLeft = *tail;
     if(*tail)
         (*tail)->pRight = root;
     *tail = root; 
 
     if(root->pRight != NULL)
         convert(root->pRight, tail);
 };
 
 BTNode* treeToDList(BTNode *root)
 {
     if(root == NULL) return NULL;
     BTNode *tail = NULL;
     convert(root, &tail);
     BTNode *pHead = tail;
     while(pHead != NULL && pHead->pLeft != NULL)
         pHead = pHead->pLeft;
     return pHead;
 }
 
 int main(){
     int TestTime = , k = ;
     while(k <= TestTime)
     {
         cout << "Test " << k++ << ":" << endl; 
 
         cout << "Create a tree: " << endl;
         BTNode *pRoot = createBinaryTree();
         printBinaryTree(pRoot);
         cout << endl; 
 
         DbList *DbListHead = treeToDList(pRoot); // pRoot translate to Double linked list.
 
         printDbList(DbListHead);
         cout << endl; 
 
         releaseDbList(DbListHead);
     }
     return ;
 }

note: 按先序输入，0表示结束。
样例输入：

a. 10 6 4 0 0 8 0 0 14 12 0 0 16 00

b. 0 (生成空树)

c. 1

d. 2 1 0 0 3 0 0

28.字符串的全排列

Go： ( 3. 字符的排列组合 )

相关例题：八皇后问题（可扩展为 n 皇后问题）

题目：8 x 8国际象棋上，摆8 个皇后，求她们任两个不同行、不同列且不在同一对角线上的摆法个数。

#include <stdio.h>
int solutionNumber = 0;
 
void print(int data[], int length)
{
	for(int i = 0; i < length; ++i)
		printf("(%d, %d)  ", i+1, data[i]+1);
	printf("\n");
}
bool judge(int data[], int length)
{
	for(int i = 0; i < length; ++i)
	{
		for(int j = i +1; j < length; ++j)
		{
			if((j - i) == (data[j] - data[i]) || (j - i) == data[i] - data[j])
				return false; // not the solution
		}
 
	}
	return true;
}
void swap(int &a, int &b) // do not forget the reference.
{
	int tem = a;
	a = b;
	b = tem;
}
 
void permutation(int data[], int length, int begin)
{
	if(begin == length-1)
	{
		if(judge(data, length))
		{
		//	print(data, length);
			++solutionNumber;
		}
		return;
	}
	for(int start = begin; start < length; ++start)
	{
		swap(data[start], data[begin]);
		permutation(data, length, begin+1);
		swap(data[start], data[begin]);
	}
}
 
int main()
{
	int columnIndex[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15};  /* 不在同行同列  */
	permutation(columnIndex, 8, 0);              /*  判断是否可以不在同一对角线  */
	printf("Number of Solution: %d\n", solutionNumber);
	return 0;
}