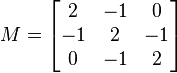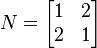Positive-definite matrix
In linear algebra, a symmetric n × n real matrix M is said to be positive definite if zTMz is positive for every non-zero columnvector
z of n real numbers. Here zT denotes thetranspose of
z.
- The real symmetric matrix
-
- is positive definite since for any non-zero column vector z with entriesa,
b and c, we have - This result is a sum of squares, and therefore non-negative; and is zero only ifa =
b = c = 0, that is, when z is zero.
- The real symmetric matrix
-
-
is not positive definite. If z is the vector
 , one has
, one has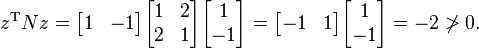
More generally, an n × n Hermitian matrix M is said to be positive definite if
z*Mz is real and positive for all non-zero complex vectors z. Here
z* denotes the conjugate transpose of z.
- 摘自:https://en.wikipedia.org/wiki/Positive_semidefinite_matrix
Positive-definite matrix的更多相关文章
- 正定矩阵(positive definite matrix)
设M是n阶方阵,如果对任何非零向量z,都有zTMz> 0,其中zT 表示z的转置,就称M正定矩阵. 正定矩阵在合同变换下可化为标准型, 即对角矩阵. 所有特征值大于零的对称矩阵也是正定矩阵. ...
- a positive definite matrix
https://en.wikipedia.org/wiki/Definite_quadratic_form https://www.math.utah.edu/~zwick/Classes/Fall2 ...
- 【线性代数】6-5:正定矩阵(Positive Definite Matrices)
title: [线性代数]6-5:正定矩阵(Positive Definite Matrices) categories: Mathematic Linear Algebra keywords: Po ...
- 正定矩阵(definite matrix)
1. 基本定义 在线性规划中,一个对称的 n×n 的实值矩阵 M,如果满足对于任意的非零列向量 z,都有 zTMz>0. 更一般地,对于 n×n 的 Hermitian 矩阵(原矩阵=共轭转置, ...
- cholesky分解
接着LU分解继续往下,就会发展出很多相关但是并不完全一样的矩阵分解,最后对于对称正定矩阵,我们则可以给出非常有用的cholesky分解.这些分解的来源就在于矩阵本身存在的特殊的 结构.对于矩阵 ...
- Mahout 系列之----共轭梯度
无预处理共轭梯度 要求解线性方程组 ,稳定双共轭梯度法从初始解 开始按以下步骤迭代: 任意选择向量 使得 ,例如, 对 若 足够精确则退出 预处理共轭梯度 预处理通常被用来加速迭代方法的收敛.要使用预 ...
- 从线性模型(linear model)衍生出的机器学习分类器(classifier)
1. 线性模型简介 0x1:线性模型的现实意义 在一个理想的连续世界中,任何非线性的东西都可以被线性的东西来拟合(参考Taylor Expansion公式),所以理论上线性模型可以模拟物理世界中的绝大 ...
- Kalman Filters
|—定位—|—蒙特卡洛方法(定位自身) | |—卡尔曼滤波器(定位其他车辆) |—高斯函数 |—循环两个过程—|—测量(测量更新) | ...
- AI人工智能专业词汇集
作为最早关注人工智能技术的媒体,机器之心在编译国外技术博客.论文.专家观点等内容上已经积累了超过两年多的经验.期间,从无到有,机器之心的编译团队一直在积累专业词汇.虽然有很多的文章因为专业性我们没能尽 ...
- Cholesky分解 平方根法
一种矩阵运算方法,又叫Cholesky分解.所谓平方根法,就是利用对称正定矩阵的三角分解得到的求解对称正定方程组的一种有效方法.它是把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解.它要 ...
随机推荐
- STL之容器(1)
STL容器类的模板 容器部分主要由头文件<vector>,<list>,<deque>,<set>,<map>,<stack>和 ...
- 三个 DAL 相关的Java代码小工具
最近在做 DAL (Data Access Layer 数据访问层) 的服务化,发现有不少地方是人工编写比较繁琐的,因此写了几个小工具来完成. 1. 从 DAO 类自动生成 CoreService ...
- 阿里云OneinStack数据库相关
阿里云OneinStack数据库相关必须进入oneinstack目录下执行相关命令 ===================================源码安装目录: Nginx:/usr/loca ...
- Dynamics AX 2012 R2 从代码中调用SSRS Report
平时,我们制作SSRS Report的方法主要有两种:使用Query或RDP.如果需要为报表传递参数,就要在代码中为报表参数赋值,然后在代码中调用报表.下面我总结下这两种报表在代码中传参和调用的方式: ...
- 如何通过iframe以post方式提交form表单
以前用过一次这种技术,这次用居然忘了,现纪录下来,下次再用就来看看. 首先在html中需要准备好form和iframe元素代码如下: <form id="speaker_form&qu ...
- winform 传值,构造函数等
窗体转换 制作一个登陆窗体,实现点击按钮关闭此窗体并打开另一个窗体 直接在按钮点击事件中,实例化一个想要打开的窗体 使用show方法打开,并把登陆窗体的visible属性改为false Form1 f ...
- Android 对电话进行监听和挂断
1.添加权限 <!--拨打电话的权限--><uses-permission android:name="android.permission.PROCESS_OUTGOIN ...
- react native 学习资料汇总
http://www.ejiakt.com/album/show/252 http://www.cocoachina.com/ios/20150408/11513.html http://www.os ...
- Java-String类的常用方法总结
一.String类String类在java.lang包中,java使用String类创建一个字符串变量,字符串变量属于对象.java把String类声明的final类,不能有类.String类对象创建 ...
- file_get_contents微信头像等待时间过长的原因
UPDATE 2016/05/13 stackoverflow上的解决方法:http://stackoverflow.com/questions/3629504/php-file-get-conten ...