Codeforces 919 E Congruence Equation

题目描述

Given an integer xx . Your task is to find out how many positive integers nn ( 1<=n<=x1<=n<=x ) satisfy

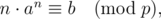 where a,b,pa,b,p are all known constants.

输入输出格式

输入格式：

The only line contains four integers a,b,p,xa,b,p,x ( 2<=p<=10^{6}+32<=p<=106+3 , 1<=a,b<p1<=a,b<p , 1<=x<=10^{12}1<=x<=1012 ). It is guaranteed that pp is a prime.

输出格式：

Print a single integer: the number of possible answers nn .

输入输出样例

输入样例#1：

2 3 5 8

输出样例#1：

2

输入样例#2：

4 6 7 13

输出样例#2：

1

输入样例#3：

233 233 10007 1

输出样例#3：

1

说明

In the first sample, we can see that n=2n=2 and n=8n=8 are possible answers.

利用同余乱搞即可，系数是mod p的同余系，指数是mod (p-1)的同余系。

不过写之前一定要想好，不然特别容易写错(细节略多)。。。

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define ll long long
#define maxn 1000010
using namespace std;
ll ans,inv[maxn],b,d;
ll ci[maxn],p,tp;

inline void init(const ll ha){
	ci[0]=1;
	for(int i=1;i<ha;i++) ci[i]=ci[i-1]*d%ha;
	inv[1]=1;
	for(int i=2;i<ha;i++) inv[i]=-inv[ha%i]*(ha/i)%ha+ha;
}

inline void solve(const ll ha){
	ll tmpc,tmpd;
	ll basec=(tp+1)/(ha-1),lefc=tp+1-basec*(ha-1);
	//basec表示指数上有多少个完整的循环节
	//lefc表示最后多出来的可以走的步数
	for(int i=p-2;i>=0;i--){
		int to=b*inv[ci[i]]%ha;
		tmpc=basec+(i<lefc);
		//tmpc是计算a^i这个数出现的次数
		tmpd=tmpc/ha+((i-to+ha)%ha<tmpc%ha);
		//因为每次指数对应的系数都会-1，
		//所以就相当于计算在系数的同余系下
		//从i开始倒退走tmp-1步能走到to多少次
		ans+=tmpd;
	}
}

int main(){
	scanf("%lld%lld%lld%lld",&d,&b,&p,&tp);
	init(p);
	solve(p);
	printf("%lld\n",ans);
	return 0;
}