javascript实现数据结构：线索二叉树

遍历二叉树是按一定的规则将树中的结点排列成一个线性序列，即是对非线性结构的线性化操作。如何找到遍历过程中动态得到的每个结点的直接前驱和直接后继(第一个和最后一个除外)?如何保存这些信息?

设一棵二叉树有n个结点，则有n-1条边(指针连线) ， 而n个结点共有2n个指针域(Lchild和Rchild) ，显然有n+1个空闲指针域未用。则可以利用这些空闲的指针域来存放结点的直接前驱和直接后继信息。

对结点的指针域做如下规定：

1.若结点有左子树，则其leftChild域指示其左孩子，否则令leftChild域指示其前驱。

2.若结点有右子树，则其rightChild域指示其右孩子，否则令其rightChild域指示其后继。

为了避免混淆，尚需改变结点结构，增加两个标志域（leftTag, rightTag），其中：

　　　　　　-- 0 leftChild域指示结点的左孩子
 leftTag --
　　　　　　 -- 1 rightChild域指示结点的前驱

　　　　　　-- 0 rightChild域指示结点的右孩子
 rightTag --
 　　　　　　-- 1 rightChild域指示结点的后继

以这种结点结构构成的二叉链表作为二叉树的存储结构，叫做线索链表，其中指向结点前驱和后继的指针，叫做线索。

加上线索的二叉树称之为线索二叉树（Threaded Binary Tree）。

对二叉树以某种次序遍历使其变为线索二叉树的过程叫做线索化。

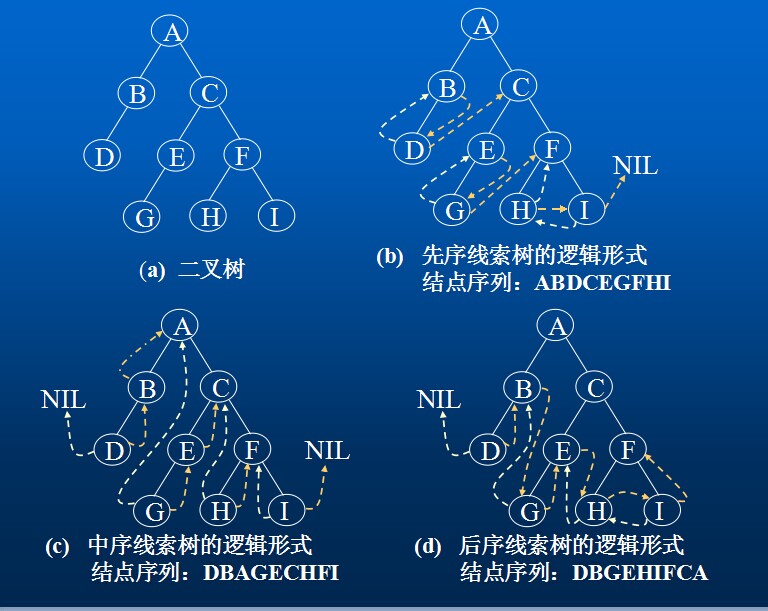
说明：画线索二叉树时，实线表示指针，指向其左、右孩子；虚线表示线索，指向其直接前驱或直接后继。

在线索树上进行遍历，只要先找到序列中的第一个结点，然后就可以依次找结点的直接后继结点直到后继为空为止。

如何在线索树中找结点的直接后继?

以图(d) ，(e)所示的中序线索树为例：

◆ 树中所有叶子结点的右链都是线索。右链直接指示了结点的直接后继，如结点G的直接后继是结点E。

◆ 树中所有非叶子结点的右链都是指针。根据中序遍历的规律，非叶子结点的直接后继是遍历其右子树时访问的第一个结点，即右子树中最左下的(叶子)结点。如结点C的直接后继：沿右指针找到右子树的根结点F，然后沿左链往下直到Ltag=1的结点即为C的直接后继结点H。

如何在线索树中找结点的直接前驱?

若结点的Ltag=1，则左链是线索，指示其直接前驱；否则，遍历左子树时访问的最后一个结点(即沿左子树中最右往下的结点) 为其直接前驱结点。

对于后序遍历的线索树中找结点的直接后继比较复杂，可分以下三种情况：

◆ 若结点是二叉树的根结点：其直接后继为空；

◆ 若结点是其父结点的左孩子或右孩子且其父结点没有右子树：直接后继为其父结点；

◆ 若结点是其父结点的左孩子且其父结点有右子树：直接后继是对其父结点的右子树按后序遍历的第一个结点。

线索化二叉树

二叉树的线索化指的是依照某种遍历次序使二叉树成为线索二叉树的过程。

线索化的过程就是在遍历过程中修改空指针使其指向直接前驱或直接后继的过程。

仿照线性表的存储结构，在二叉树的线索链表上也添加一个头结点head，头结点的指针域的安排是：

◆ Lchild域：指向二叉树的根结点；

◆ Rchild域：指向中序遍历时的最后一个结点；

◆ 二叉树中序序列中的第一个结点Lchild指针域和最后一个结点Rchild指针域均指向头结点head。

如同为二叉树建立了一个双向线索链表，对一棵线索二叉树既可从头结点也可从最后一个结点开始按寻找直接后继进行遍历。显然，这种遍历不需要堆栈。

线索二叉树的遍历

在线索二叉树中，由于有线索存在，在某些情况下可以方便地找到指定结点在某种遍历序列中的直接前驱或直接后继。此外，在线索二叉树上进行某种遍历比在一般的二叉树上进行这种遍历要容易得多，不需要设置堆栈，且算法十分简洁。

线索二叉树的相关代码实现：

 var LINK = 0;
 var THREAD = 1;

 function BinaryThreadTree_inOrder(data, leftChild, rightChild) {
     this.data = data;
     this.leftChild = leftChild || null;
     this.rightChild = rightChild || null;
     // 左右标记
     this.leftTag = this.rightTag = undefined;
 }
 BinaryThreadTree_inOrder.prototype = {
     constructor: BinaryThreadTree_inOrder,
     // 中序线索二叉树的遍历
     inOrderTraverse_thread: function (visit) {
         var p = this.leftChild;

         while (p != this) {
             while (p.leftTag === LINK) p = p.leftChild;

             if (visit(p.data) === false) return;

             while (p.rightTag == THREAD && p.rightChild != this) {
                 p = p.rightChild;
                 visit(p.data);
             }
             p = p.rightChild;
         }
     },
     // 中序线索化
     inOrderThreading: function () {
         return inOrderThreading(this);
     },
     // 在当前结点插入子树x，p代表当前结点
     insertSubTree: function (xTree) {
         var s, q;
         // x作为p的左子树
         if (this.leftTag === THREAD) {
             s = this.leftChild; // s为p的前驱
             this.leftTag = LINK;
             this.leftChild = xTree;
             q = xTree;

             while (q.leftChild && q.leftTag === LINK) q = q.leftChild;
             // 找到子树中的最左结点，并修改其前驱指向s
             q.leftChild = s;
             xTree.rightTag = THREAD;
             // x的后继指向p
             xTree.rightChild = this;
         }
         // x作为p的右子树
         else if (this.rightTag === THREAD) {
             // s为p的后继
             s = this.rightChild;
             this.rightTag = LINK;
             this.rightChild = xTree;
             q = xTree;

             while (q.leftChild && q.leftTag === LINK) q = q.leftChild;
             // 找到子树中的最左结点，并修改其前驱指向p
             q.leftChild = this;
             xTree.rightTag = THREAD;
             // x的后继指向p的后继
             xTree.rightChild = s;
         }
         // x作为p的左子树，p的左子树作为x的右子树
         else {
             s = this.leftChild;
             var t = s;

             while (t.leftChild && t.leftTag === LINK) t = t.leftChild;
             // 找到p的左子树的最左结点t和前驱u
             var u = t.leftChild;
             this.leftChild = xTree;
             xTree.rightTag = LINK;
             // x作为p的左子树，p的左子树作为x的右子树
             xTree.rightChild = s;
             t.leftChild = xTree;
             q = xTree;

             while (q.leftChild && q.leftTag === LINK) q = q.leftChild;
             // 找到子树中的最左结点，并修改其前驱指向u
             q.leftChild = u;
         }
     }
 };

 // 二叉树中序线索化
 function inOrderThreading(tree) {
     var threadTree = new BinaryThreadTree();
     threadTree.leftTag = LINK;
     threadTree.rightTag = THREAD;
     // 右指针回指
     threadTree.rightChild = threadTree;

     var pre;
     // 若二叉树为空，左指针回指
     if (!tree) threadTree.leftChild = threadTree;
     else {
         threadTree.leftChild = tree;
         pre = threadTree;
         inThreading(tree);  // 中序遍历进行中序线索化
         // 最后一个结点线索化
         pre.rightChild = threadTree;
         pre.rightTag = THREAD;
         threadTree.rightChild = pre;
     }

     return threadTree;

     function inThreading(p) {
         if (!p) return;

         inThreading(p.leftChild);   // 左子树线索化
         // 前驱线索
         if (!p.leftChild) {
             p.leftTag = THREAD;
             p.leftChild = pre;
         }
         // 后继线索
         if (!pre.rightChild) {
             pre.rightTag = THREAD;
             pre.rightChild = p;
         }
         pre = p;
         inThreading(p.rightChild);  // 右子树线索化
     }
 }