linux基础——磁盘分区和yum安装

第一部分

1) 开启Linux系统前添加一块大小为15G的SCSI硬盘

 

2) 开启系统，右击桌面，打开终端

 

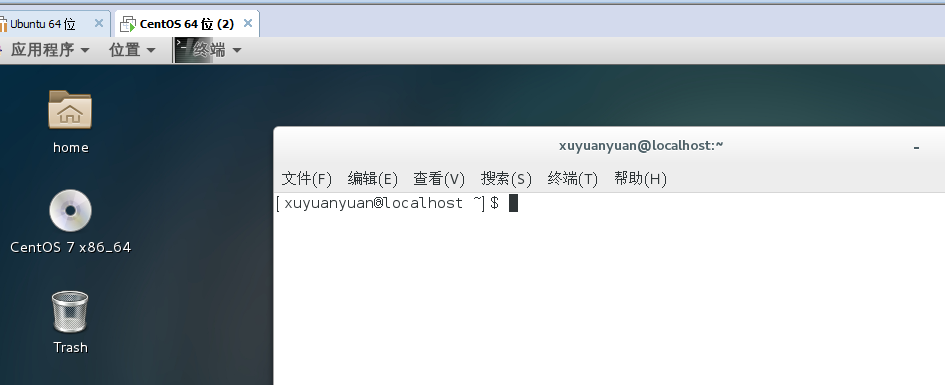
3) 为新加的硬盘分区，一个主分区大小为5G，剩余空间给扩展分区，在扩展分区上划分1个逻辑分区，大小为5G

fdisk -l

fdisk /dev/sdb

p 查看

n 新建

   p  主分区

   e  扩展

   l  逻辑

 

4) 格式化主分区为ext3系统

mkfs.ext3 /dev/sdb1

 

5) 将逻辑分区设置为交换分区

mkswap /dev/sdb5

 

6) 启用上一步的交换分区

swapon -a /dev/sdb5

 

7) 查看交换分区的状态

 

 

 

第二部分

（1）free命令查看内存
操作：free 和内存的使用情况
       free -m （内存的使用情况，-m 　以MB为单位显示内存使用情况。）

 

（2）整理buffer与cache的作用
buffers：还没有被写入磁盘的东西，是指用来给块设备做的缓冲大小，它只记录文件系统的metadata以及 tracking in-flight pages.
cached：已经从内存中读到内存中的东西，是用来给文件做缓冲。
也就是说：buffers是用来存储，目录里面有什么内容，权限等等。
而cached直接用来记忆我们打开的文件，如果你想知道它是不是真的生效，可以试一下，先后执行两次命令#man X ,就可以明显的感觉到第二次的开打的速度快很多。

（3）计算真实的内存使用率
centos 7.3版本free计算公式used+free+
buffer/cache=total
available是开启一个新程序能够使用的最大内存

(total-(free buffer cache))/total

 

第三部分

dd命令测试硬盘速度

 

 

 

第四部分

1、查询firewall进程，然后杀死

 操作：

ps aux查看所有进程

ps aus | grep firewall 是过滤查看firewall进程

查看firewall的ID号，然后kill -9 进程号 或者pkill -9 firewall即可杀死
补充：不想在命令显示在进程里，可以加上&符号
例：以火狐举例，firefox &即可让命令在后台运行
可以使用jobs查看
杀死后台运行的话，可以pkill -9 firefox

 

 

 

 

第五部分

1、查看centos 7 x86-64的文件在哪

输入ls Packages可查看到在该目录下有一堆文件包

 

 

 

 

 

rpm命令
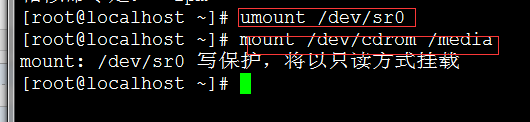
1) 挂载光盘文件到/media目录

umount /dev/sr0
mount /dev/cdrom /media

 

2) 进去/media目录下的Packages目录

 cd /media/Packages/

 

3) 查看系统已安装的所有rpm包

rpm -qa

 

4) 查看系统是否安装dhcp软件包

rpm -qa |grep dhcp

 

5) 安装dhcp软件包

rpm -ivh dhcp-*

 

6) 查看dhcp软件包的信息

 rpm -qi dhcp

 

7) 查看dhcp软件包中所包含的所有文件

 rpm -ql dhcp

 

8) 查看/bin/ls文件是由哪个软件包产生

rpm -qf /bin/ls 来查看

which ls

 

9) 卸载dhcp软件包

 rqm -e --nodeps dhcp-common再使用rpm -qa |grep dhcp查看是否已经卸载完毕(--nodeps是忽略依赖关系）

 

 

 

 

第六部分

yum命令
1） 自定义yum仓库：create repo

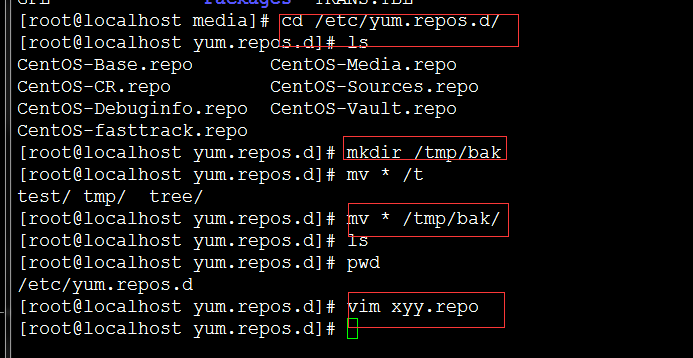
2） 自定义repo文件 

 

 

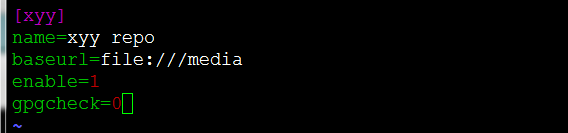
3） 使用yum命令安装httpd软件包

yum install httpd  输入y确定安装，或者yum -y install httpd不提示是否安装，直接一次性安装

 

 

4） 卸载httpd软件包：

yum -y erase httpd

 

 

5） 使用yum安装组件'KDE 桌面'：yum –y groupinstall 组件名

 yum –y groupinstall KDE Plasma Workspaces

 

6) 使用yum删除组件‘KDE 桌面’:yum –y groupremove 组件名

yum –y groupremove KDE Plasma Workspaces

7） 清除yum缓存：

yum clean all

 

8） 使用yum查找软件包：yum search 软件包名

 

第七部分

源码安装python