【BZOJ2818】Gcd [莫比乌斯反演]

Gcd

Time Limit: 10 Sec  Memory Limit: 256 MB
[Submit][Status][Discuss]

Description

　　给定整数N，求1<=x,y<=N且Gcd(x,y)为素数的
　　数对(x,y)有多少对.

Input

　　一个整数N

Output

　　如题

Sample Input

　　4

Sample Output

　　4

HINT

　　1<=N<=10^7

Solution

　　直接莫比乌斯反演即可。

　　

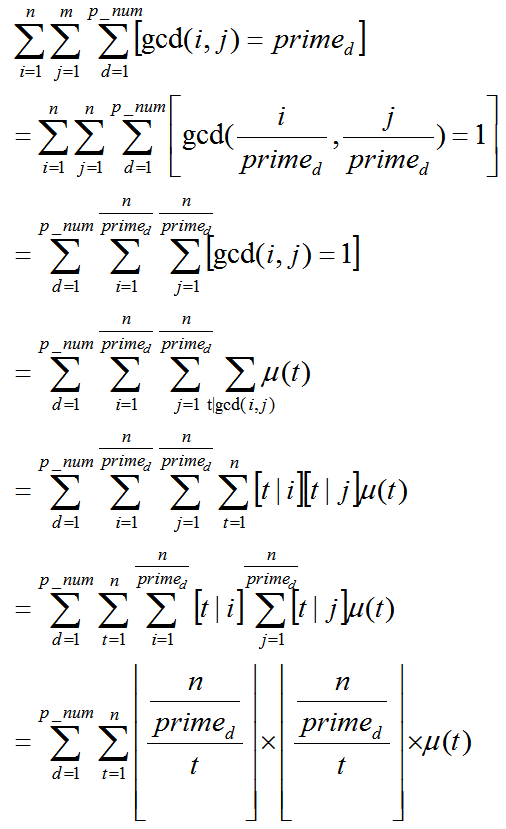
　　然后对于这个式子，我们下界分块一下即可。

Code

 #include<iostream>
 #include<string>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;
 typedef long long s64;

 const int ONE = 1e7+;

 int T;
 int n,m;
 bool isp[ONE];
 int prime[],p_num;
 int miu[ONE],sum_miu[ONE];
 s64 Ans;

 int get()
 {
         int res=,Q=;  char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }

 void Getmiu(int MaxN)
 {
         miu[] = ;
         for(int i=; i<=MaxN; i++)
         {
             if(!isp[i])
                 isp[i] = , prime[++p_num] = i, miu[i] = -;
             for(int j=; j<=p_num, i*prime[j]<=MaxN; j++)
             {
                 isp[i * prime[j]] = ;
                 if(i % prime[j] == )
                 {
                     miu[i * prime[j]] = ;
                     break;
                 }
                 miu[i * prime[j]] = -miu[i];
             }
             miu[i] += miu[i-];
         }
 }

 int main()
 {
         n=get();
         Getmiu(n);
         for(int d=; d<=p_num; d++)
         {
             if(prime[d] > n) break;
             int N = n/prime[d];
             for(int i=,j=; i<=N; i=j+)
             {
                 j = min(N, N/(N/i));
                 Ans += (s64)(N/i) * (N/i) * (miu[j] - miu[i-]);
             }
         }

         printf("%lld",Ans);
 }