四则运算(Java) 陈志海 邓宇

目录

• Github项目地址
• PSP表格
• 功能要求
  • 题目
  • 功能(已全部实现)
• 效能分析
• 设计实现过程
  • 数值生成
  • 算式生成
  • 问题集生成
• 设计实现过程
• 代码说明
• 测试运行
• 代码覆盖率
• 项目小结

---

Github项目地址

Arithmetic

PSP表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	40	40
· Estimate	· 估计这个任务需要多少时间	40	40
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	60	120
· Design Spec	· 生成设计文档	39	30
· Design Review	· 设计复审 (和同事审核设计文档)	20	50
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	20	20
· Design	· 具体设计	60	120
· Coding	· 具体编码	500	720
· Code Review	· 代码复审	60	60
· Test	· 测试（自我测试，修改代码，提交修改）	90	120
Reporting	报告
· Test Report	· 测试报告	40	40
· Size Measurement	· 计算工作量	20	20
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	60	80
	合计	1000	1400

功能要求

题目

实现一个自动生成小学四则运算题目的命令行程序

功能(已全部实现)

1. 使用 -n 参数控制生成题目的个数。
2. 使用 -r 参数控制题目中数值（自然数、真分数和真分数分母）的范围。
3. 生成的题目中计算过程不能产生负数，也就是说算术表达式中如果存在形如e1 − e2的子表达式，那么e1 ≥ e2。
4. 生成的题目中如果存在形如e1 ÷ e2的子表达式，那么其结果应是真分数。
5. 每道题目中出现的运算符个数不超过3个。
6. 程序一次运行生成的题目不能重复，即任何两道题目不能通过有限次交换+和×左右的算术表达式变换为同一道题目。
7. 在生成题目的同时，计算出所有题目的答案，并存入执行程序的当前目录下的Answers.txt。
8. 程序应能支持一万道题目的生成。
9. 程序支持对给定的题目文件和答案文件，判定答案中的对错并进行数量统计，统计结果输出到文件Grade.txt。

效能分析

参数如下图，n值为100000（即10W道），

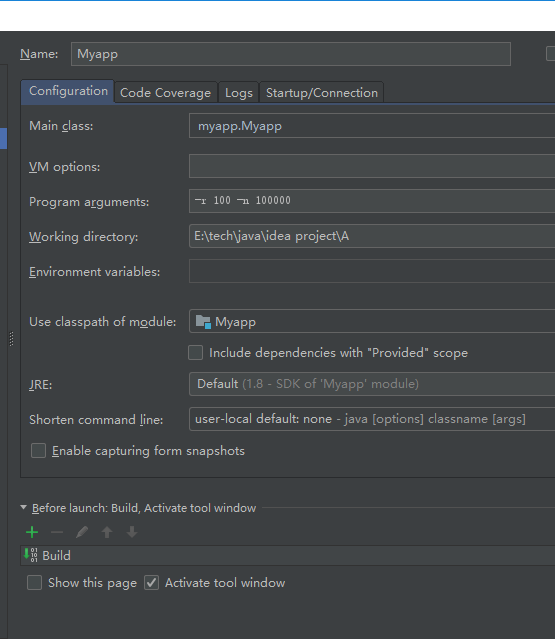
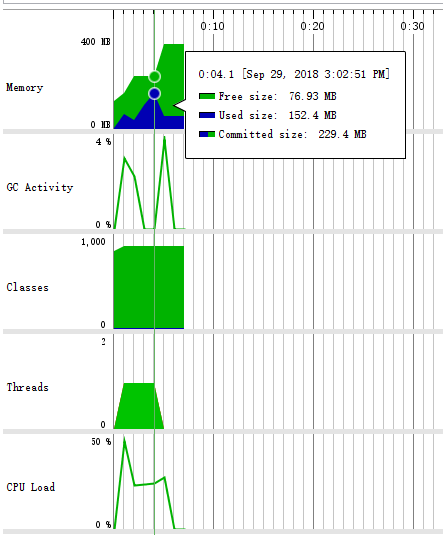
观察下图的性能曲线，可以看出大概需要8秒钟时间生成，使用内存峰值大约在150MB左右。

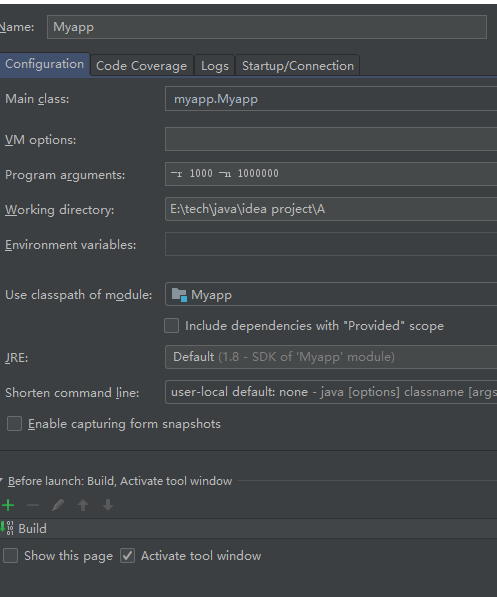
我们再次提高n值上限（1000000 100W道），适当调高r值（1000）。

可以看出大概需要54秒钟生成，使用内存峰值大约在840MB左右。

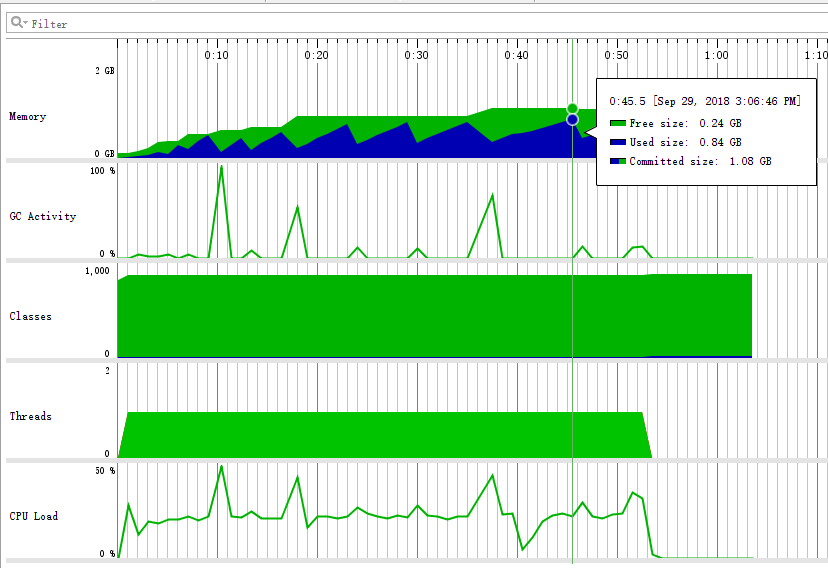
我们觉得这个运行时间有点过长，试着增大r值，看看题目树生成碰撞导致的效率减慢占比是多少。

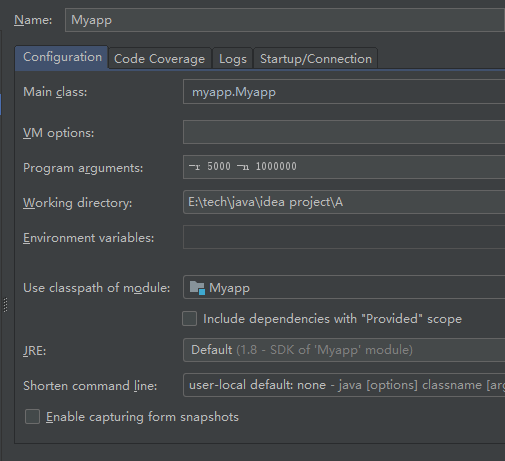
我们的r值增大到5000，生成时间就从54秒下降到29秒，有一个很大的改进。

设计实现过程

数值生成

题目提及了三种数字的表示形式，一种是整数（例：3），一种是分数（例：3/5），一种是带分数（例：2’3/5）。这三种数字我们统一使用一个Num类，并提供随机方式生成，然后根据不同部分的值产生不同的导出结果。Num类维护一个int类型的num[3]数组，刚开始被初始化全0。

然后生成逻辑如下：

1. 获得整数上限r
2. 对于分母部分获得随机[0,r]内的一个数
3. 如果分母生成值为0，将分子部分赋给整数部分，此时我们获得了一个全为0的数，结束生成。
4. 如果分母生成值不为0，对于分子部分获得随机[0,r*r]内的一个数，此时也保证了最后生成的结果绝对不会大于r。
5. 将分子/分母的值赋给整数部分，剩余部分赋给分子，保证带分数中分子不会大于等于分母。
6. 如果此时分子生成值为0，将分母也置为0，此时我们获得了一个全为0的数，结束生成。
7. 对分子和分母进行辗转相除法，获得最简分式。结束生成。

然后在Num类也内建了一个函数，用来返回字符串类型的数值表达式：

1. 如果分母或分子部分为0，直接返回整数部分。
2. 如果整数部分为0，因为分子部分也不为0，直接返回一个分式形式。
3. 否则返回一个带分数形式。

然后封包了对应的加减乘除法，每次计算返回一个新的Num对象，包含计算完毕的结果。

算式生成

生成算式简单，但是要在生成之后判重需要花费心思去思索。

我们采用了二叉树的数据结构来存储整个算式，在非叶子节点存储运算符，叶子节点存储数值。这样，我们就很容易得到一颗符合波兰表达式的二叉树。我们计算和判重只需要对整个二叉树进行一次前缀遍历即可。

结对约定了二叉树的运算符拓展必然是只拓展二叉树的左子树，这样的约定既方便了代码的生成，使得递归生成的实现十分简洁。这样也同时避免了另外一个问题，就是对于加减法或乘除法来说，有个暗含的优先计算减再算加，先计算除再算乘的细节。例如，1+2的外面套一层括号，对整个式子的结果不会有影响，而1-2的外面套一层括号，则会有影响，故要先算减再算加。

我们使用一个运算符从数字映射到字符串加减乘除的常量数组存储在CTree类中，对于每一次生成，有以下方式初始化：

1. 获得父对象的指针，深度，和整数上限r。
2. 记录父对象的指针，如果深度为0，对本对象管理下的Num类对象进行初始化构造，本类构造结束。
3. 如果深度不为0，对于运算符部分获得随机[0,3]内的一个数，对于加减乘除，对左子树迭代传递构造，右子树进行深度为0的传递构造，参考2。

这样我们就可以获得一颗符合上述节点描述的二叉树了。之后是判重部分的逻辑：

维护了三个方法

• isNumber()用左右子树是否有对象指向来确认该节点是不是数值节点。
• isRoot()用父对象是否有对象指向来确定该节点是不是根节点。
• equals()比较树是否相同，暴露供外部调用。

利用上面三个方法和Num的部分函数来进行判重。

1. 如果节点类型不同，直接认为是不同的。
2. 如果是数值节点，直接判定Num类中num三个部分是否相同（num已经是最简式）来判定是否重合。
3. 如果是运算符节点，判定运算符类型是否相同来判定是否重合。

问题集生成

在CTree上再封装一层，我们利用Calculation类来管理二叉树，同时该类也是判重的接口，以及运算符个数的生成者。

问题集的处理，因为在Ctree部分处理重合的算法选择的好，这部分就不需要太费劲。我们直接建立一个HashSet，Calculation类重写了hashCode()函数，返回答案的字符串hashCode，来第一步去重。若答案一样，也就是hashCode一样，HashSet会调用Calculation类的equals退化成链表保存。

设计实现过程

面向对象编程，将文件按功能抽离成类，每个类暴露对应的函数。

代码说明

数值生成逻辑：

    public Num(int r) {
        num = new int[3];
        num[2] = (int)(Math.random() * r);

        if(num[2] == 0) {
            num[0] = num[1];
            num[1] = 0;
        } else {
            num[1] = (int)(Math.random() * r) * (int)(Math.random() * r) % num[2] * r;

            num[0] = num[1] / num[2];
            num[1] = num[1] % num[2];
            if(num[1] == 0) {
                num[2] = 0;
            }

            if(num[1] != 0 && num[2] != 0)
            {
                int gcdNumber = gcd(num[1], num[2]);
                num[1] /= gcdNumber;
                num[2] /= gcdNumber;
            }
        }
    }

数值返回逻辑：

    public String getFromatNumber() {
        String str = new String();
        if(num[2] == 0) {
            str += String.valueOf(num[0]);
        } else {
        	if(num[1] == 0) {
        		str += String.valueOf(num[0]);
        	}
        	else if(num[0] != 0) {
                str += String.valueOf(num[0]) + '\''
                        + String.valueOf(num[1]) + '/' + String.valueOf(num[2]);
            } else {
                str += String.valueOf(num[1]) + '/' + String.valueOf(num[2]);
            }
        }

        return str;
    }

算式生成逻辑：

    public CTree(CTree parent, int depth, int r) {
        this.parent = parent;
        if(depth == 0) {
            lchild = null;
            rchild = null;
            num = new Num(r);
        } else {
            operationType = (int)(Math.random() * 4);
            lchild = new CTree(this, depth - 1, r);
            rchild = new CTree(this, 0, r);
        }
    }

算式判重逻辑：

    public boolean equals(CTree s) { //比较树是否相同 ,不区分左右子树位置不同
        if(isNumber() != s.isNumber()) {
            return false;
        }
        if(isNumber() == true) {
            return num.equals(s.num);
        }
        if(operationType != s.operationType) {
            return false;
        }

        return (lchild.equals(s.lchild) && rchild.equals(s.rchild))
                 || (lchild.equals(s.rchild) && rchild.equals(s.lchild));
    }

测试运行

生成文件

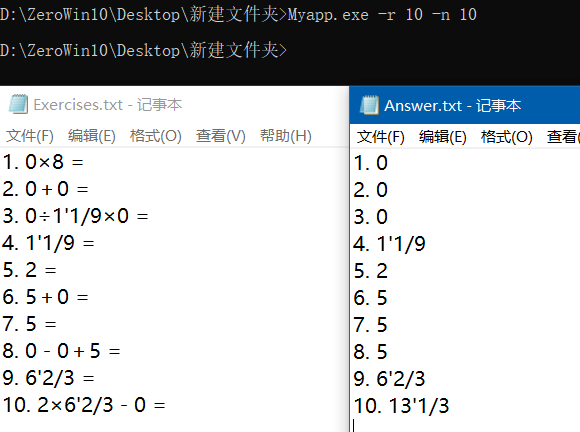
批改

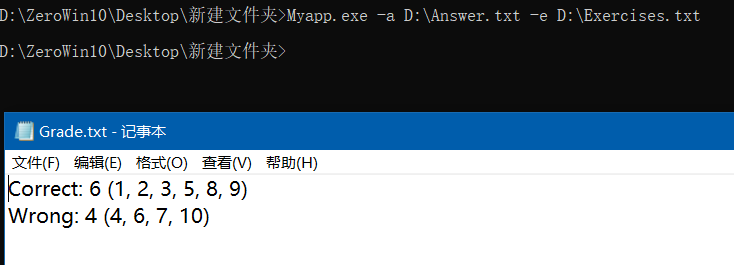
代码覆盖率

项目小结

此次的结对编程，由陈志海同学负责前期架构搭建，项目测试，而我负责前期编码和博文编写。

我们讨论项目基本构思，在每一个点都是先做好大概设计，每一个类需要有什么方法。还讨论了数值生成如何操作，才能保证在范围内；二叉树存放算式的每一部分该怎么设计，才能尽可能准确高效的生成一个算式；整个计算过程中出现负值的处理等等。

然后陈志海同学把架构交给我，两个协作着，我来实现具体细节，他来在每一步编写完毕后提出问题，解决一些明显的逻辑BUG。我来提供一些算法和结构上的优化。

在项目大体编写完毕后，由陈志海同学进行项目测试，解决一些细节和用户体验方面的问题，同时完成了批改的功能。

我从此次项目中收获到了，两个人的力量，不仅仅体现在编码的速度方面，对于提升代码质量、技术精进方面都有很大的助益。同时明白了团队约定代码规范，思路交流方面是需要多多注意的。