数据结构与算法---树结构(Tree structure)
为什么需要树这种数据结构
数组存储方式的分析
- 优点:通过下标方式访问元素,速度快。对于有序数组,还可使用二分查找提高检索速度。
- 缺点:如果要检索具体某个值,或者插入值(按一定顺序)会整体移动,效率较低。
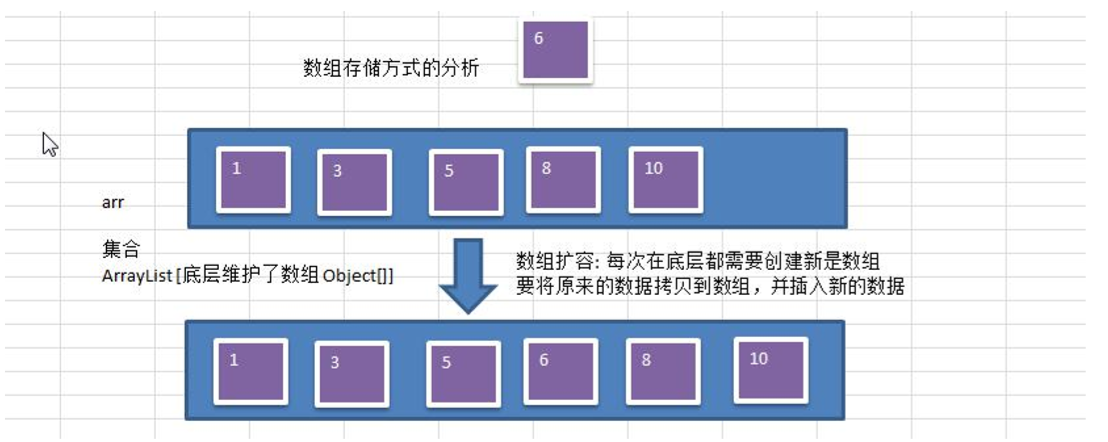
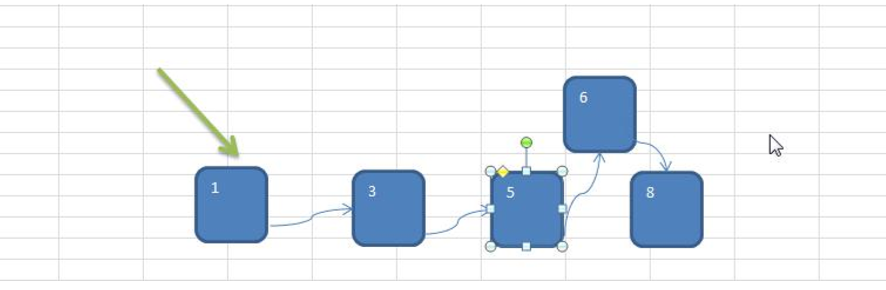
链式存储方式的分析
- 优点:在一定程度上对数组存储方式有优化(比如:插入一个数值节点,只需要将插入节点,链接到链表中即可, 删除效率也很好)。
- 缺点:在进行检索时,效率仍然较低,比如(检索某个值,需要从头节点开始遍历)
树存储方式的分析
能提高数据存储,读取的效率, 比如利用 二叉排序树(Binary Sort Tree),既可以保证数据的检索速度,同时也可以保证数据的插入,删除,修改的速度。

树结构示意图
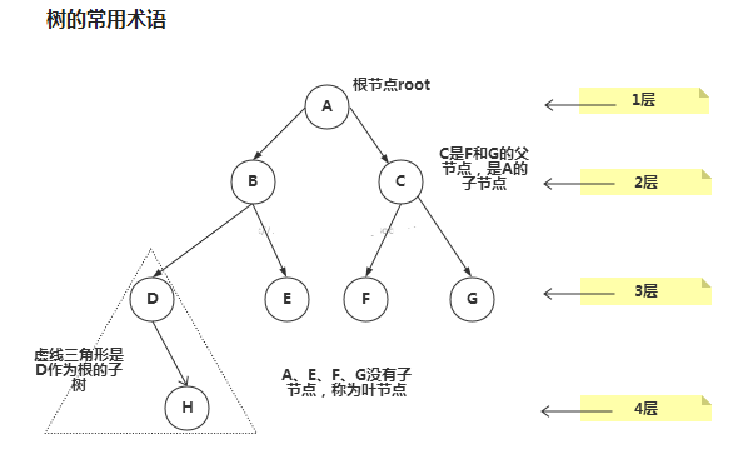

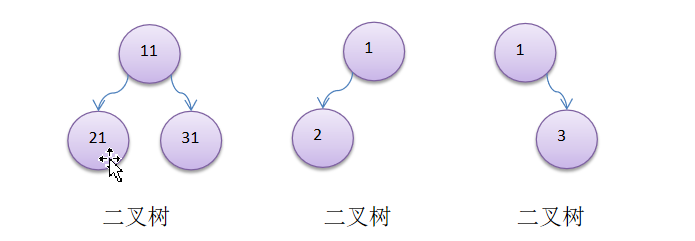
二叉树的概念
- 树有很多种,每个节点最多只能有两个子节点的一种形式称为二叉树。
- 二叉树的子节点分为左节点和右节点。
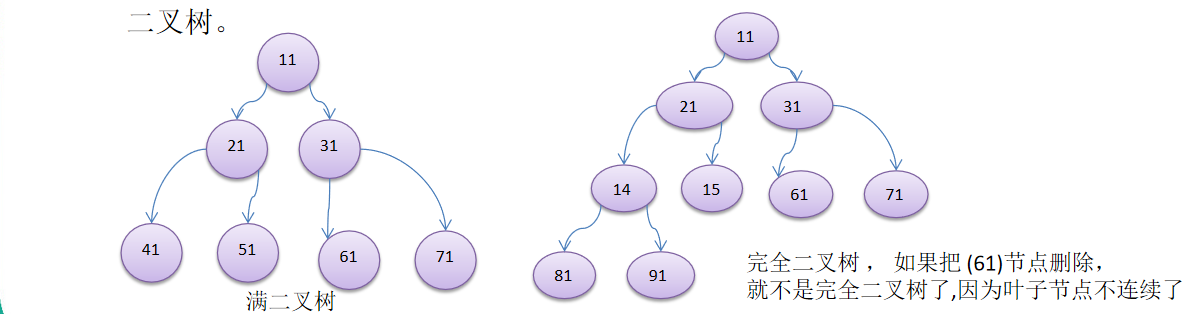
- 如果该二叉树的所有叶子节点都在最后一层,并且结点总数= 2^n -1 , n 为层数,则我们称为满二叉树。
- 如果该二叉树的所有叶子节点都在最后一层或者倒数第二层,而且最后一层的叶子节点在左边连续,倒数第二层的叶子节点在右边连续,我们称为完全二叉树。
二叉树遍历的说明
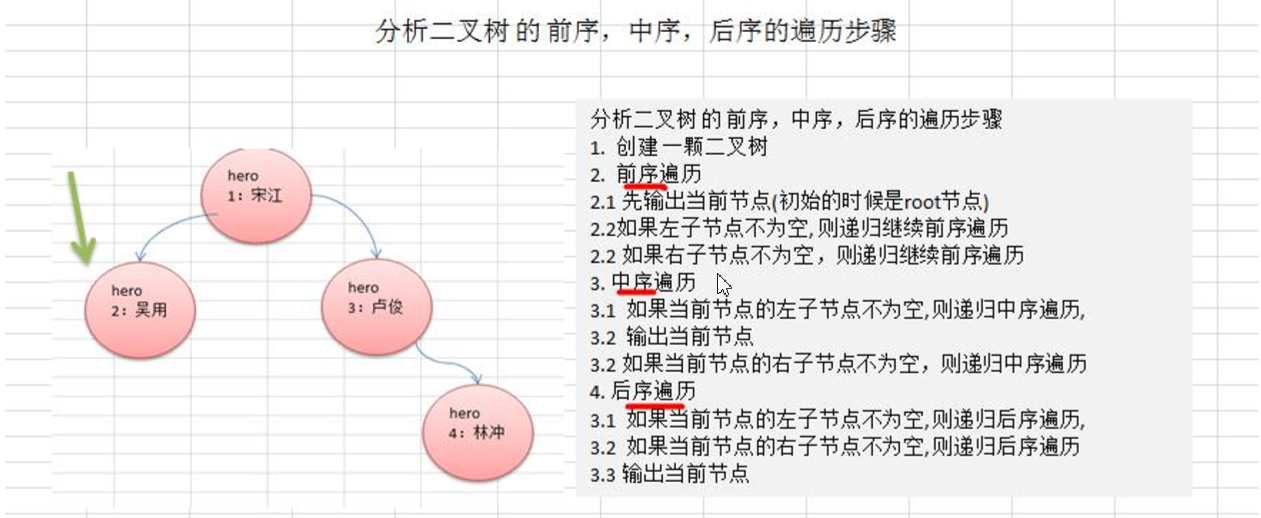
前序遍历: 先输出父节点,再遍历左子树和右子树
中序遍历: 先遍历左子树,再输出父节点,再遍历右子树
后序遍历: 先遍历左子树,再遍历右子树,最后输出父节点
小结: 看输出父节点的顺序,就确定是前序,中序还是后序
示例:
将下列二叉树 前序、中序、后序输出
package com.tree; /**
* Created by wanbf on 2019/7/9.
*/ public class BinaryTreeDemo { public static void main(String[] args) {
//先需要创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
//创建需要的结点
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
//HeroNode node5 = new HeroNode(5, "关胜"); //说明,我们先手动创建该二叉树,后面我们学习递归的方式创建二叉树
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
//node3.setLeft(node5);
binaryTree.setRoot(root); //测试
System.out.println("前序遍历"); // 1,2,3,4
binaryTree.preOrder(); //测试
System.out.println("中序遍历");
binaryTree.infixOrder(); // 2,1,3,4 System.out.println("后序遍历");
binaryTree.postOrder(); // 2,4,3,1 } } //定义BinaryTree 二叉树
class BinaryTree {
private HeroNode root; public void setRoot(HeroNode root) {
this.root = root;
}
//前序遍历
public void preOrder() {
if(this.root != null) {
this.root.preOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
} //中序遍历
public void infixOrder() {
if(this.root != null) {
this.root.infixOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
//后序遍历
public void postOrder() {
if(this.root != null) {
this.root.postOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
} //先创建HeroNode 结点
class HeroNode {
private int no;
private String name;
private HeroNode left; //默认null
private HeroNode right; //默认null
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
} //编写前序遍历的方法
public void preOrder() {
System.out.println(this); //先输出父结点
//递归向左子树前序遍历
if(this.left != null) {
this.left.preOrder();
}
//递归向右子树前序遍历
if(this.right != null) {
this.right.preOrder();
}
}
//中序遍历
public void infixOrder() { //递归向左子树中序遍历
if(this.left != null) {
this.left.infixOrder();
}
//输出父结点
System.out.println(this);
//递归向右子树中序遍历
if(this.right != null) {
this.right.infixOrder();
}
}
//后序遍历
public void postOrder() {
if(this.left != null) {
this.left.postOrder();
}
if(this.right != null) {
this.right.postOrder();
}
System.out.println(this);
}
}
代码
前序遍历
HeroNode [no=1, name=宋江]
HeroNode [no=2, name=吴用]
HeroNode [no=3, name=卢俊义]
HeroNode [no=4, name=林冲]
中序遍历
HeroNode [no=2, name=吴用]
HeroNode [no=1, name=宋江]
HeroNode [no=3, name=卢俊义]
HeroNode [no=4, name=林冲]
后序遍历
HeroNode [no=2, name=吴用]
HeroNode [no=4, name=林冲]
HeroNode [no=3, name=卢俊义]
HeroNode [no=1, name=宋江]
输出
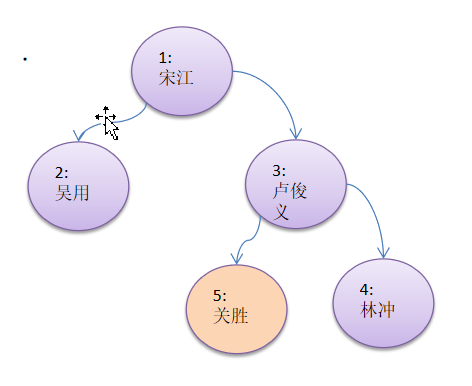
前上图的 3号节点 "卢俊" , 增加一个左子节点 [5, 关胜]
使用前序,中序,后序遍历,请写出各自输出的顺序是什么?
public static void main(String[] args) {
//先需要创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
//创建需要的结点
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
HeroNode node5 = new HeroNode(5, "关胜");
//说明,我们先手动创建该二叉树,后面我们学习递归的方式创建二叉树
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
//测试
System.out.println("前序遍历"); // 1,2,3,5,4
binaryTree.preOrder();
//测试
System.out.println("中序遍历");
binaryTree.infixOrder(); // 2,1,5,3,4
System.out.println("后序遍历");
binaryTree.postOrder(); // 2,5,4,3,1
}
代码
前序遍历
HeroNode [no=1, name=宋江]
HeroNode [no=2, name=吴用]
HeroNode [no=3, name=卢俊义]
HeroNode [no=5, name=关胜]
HeroNode [no=4, name=林冲]
中序遍历
HeroNode [no=2, name=吴用]
HeroNode [no=1, name=宋江]
HeroNode [no=5, name=关胜]
HeroNode [no=3, name=卢俊义]
HeroNode [no=4, name=林冲]
后序遍历
HeroNode [no=2, name=吴用]
HeroNode [no=5, name=关胜]
HeroNode [no=4, name=林冲]
HeroNode [no=3, name=卢俊义]
HeroNode [no=1, name=宋江]
输出
二叉树-查找指定节点
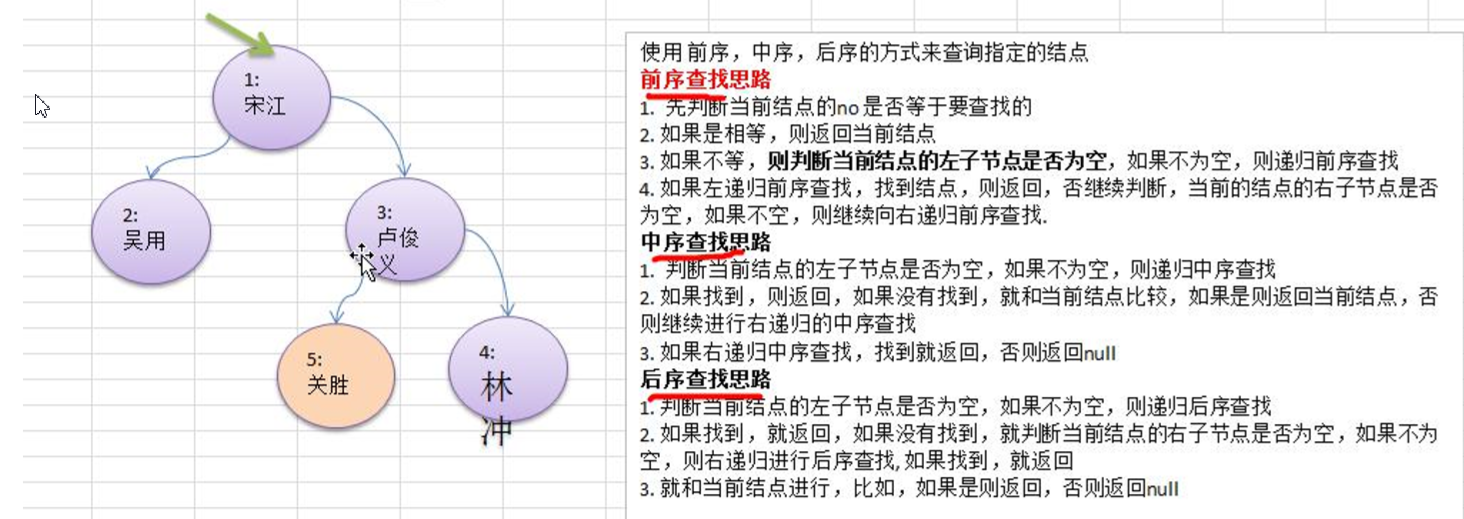
1.编写前序查找,中序查找和后序查找的方法。
2.并分别使用三种查找方式,查找 heroNO = 5 的节点
3.并分析各种查找方式,分别比较了多少次
思路分析
/**
* Created by wanbf on 2019/7/9.
*/
public class BinaryTreeDemo { public static void main(String[] args) {
//先需要创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
//创建需要的结点
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
HeroNode node5 = new HeroNode(5, "关胜"); //说明,我们先手动创建该二叉树,后面我们学习递归的方式创建二叉树
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root); //前序遍历
//前序遍历的次数 :4
System.out.println("前序遍历方式~~~");
HeroNode resNode = binaryTree.preOrderSearch(5);
if (resNode != null) {
System.out.printf("找到了,信息为 no=%d name=%s", resNode.getNo(), resNode.getName());
} else {
System.out.printf("没有找到 no = %d 的英雄", 5);
} //中序遍历查找
//中序遍历3次
System.out.println("中序遍历方式~~~");
HeroNode resNode = binaryTree.infixOrderSearch(5);
if (resNode != null) {
System.out.printf("找到了,信息为 no=%d name=%s", resNode.getNo(), resNode.getName());
} else {
System.out.printf("没有找到 no = %d 的英雄", 5);
} //后序遍历查找
//后序遍历查找的次数 2次
System.out.println("后序遍历方式~~~");
HeroNode resNode = binaryTree.postOrderSearch(5);
if (resNode != null) {
System.out.printf("找到了,信息为 no=%d name=%s", resNode.getNo(), resNode.getName());
} else {
System.out.printf("没有找到 no = %d 的英雄", 5);
}
} } //定义BinaryTree 二叉树
class BinaryTree {
private HeroNode root; public void setRoot(HeroNode root) {
this.root = root;
}
//前序遍历查找
public HeroNode preOrderSearch(int no) {
if(root != null) {
return root.preOrderSearch(no);
} else {
return null;
}
}
//中序遍历查找
public HeroNode infixOrderSearch(int no) {
if(root != null) {
return root.infixOrderSearch(no);
}else {
return null;
}
}
//后序遍历查找
public HeroNode postOrderSearch(int no) {
if(root != null) {
return this.root.postOrderSearch(no);
}else {
return null;
}
}
} //先创建HeroNode 结点
class HeroNode {
private int no;
private String name;
private HeroNode left; //默认null
private HeroNode right; //默认null
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
//前序遍历查找
/**
*
* @param no 查找no
* @return 如果找到就返回该Node ,如果没有找到返回 null
*/
public HeroNode preOrderSearch(int no) {
System.out.println("进入前序遍历");
//比较当前结点是不是
if(this.no == no) {
return this;
}
//1.则判断当前结点的左子节点是否为空,如果不为空,则递归前序查找
//2.如果左递归前序查找,找到结点,则返回
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if(resNode != null) {//说明我们左子树找到
return resNode;
}
//1.左递归前序查找,找到结点,则返回,否继续判断,
//2.当前的结点的右子节点是否为空,如果不空,则继续向右递归前序查找
if(this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
} //中序遍历查找
public HeroNode infixOrderSearch(int no) {
//判断当前结点的左子节点是否为空,如果不为空,则递归中序查找
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("进入中序查找");
//如果找到,则返回,如果没有找到,就和当前结点比较,如果是则返回当前结点
if(this.no == no) {
return this;
}
//否则继续进行右递归的中序查找
if(this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode; } //后序遍历查找
public HeroNode postOrderSearch(int no) { //判断当前结点的左子节点是否为空,如果不为空,则递归后序查找
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if(resNode != null) {//说明在左子树找到
return resNode;
} //如果左子树没有找到,则向右子树递归进行后序遍历查找
if(this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("进入后序查找");
//如果左右子树都没有找到,就比较当前结点是不是
if(this.no == no) {
return this;
}
return resNode;
} }
代码
前序遍历方式~~~
进入前序遍历
进入前序遍历
进入前序遍历
进入前序遍历
找到了,信息为 no=5 name=关胜中序遍历方式~~~
进入中序查找
进入中序查找
进入中序查找
找到了,信息为 no=5 name=关胜后序遍历方式~~~
进入后序查找
进入后序查找
找到了,信息为 no=5 name=关胜
输出
二叉树-删除节点
定义:
- 如果删除的节点是叶子节点,则删除该节点
- 如果删除的节点是非叶子节点,则删除该子树.
思路分析:

实现删除代码:
//定义BinaryTree 二叉树
class BinaryTree {
private HeroNode root; public void setRoot(HeroNode root) {
this.root = root;
} //删除结点
public void delNode(int no) {
if(root != null) {
//如果只有一个root结点, 这里立即判断root是不是就是要删除结点
if(root.getNo() == no) {
root = null;
} else {
//递归删除
root.delNode(no);
}
}else{
System.out.println("空树,不能删除~");
}
}
}
class HeroNode {
private int no;
private String name;
private HeroNode left; //默认null
private HeroNode right; //默认null
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
//递归删除结点
//1.如果删除的节点是叶子节点,则删除该节点
//2.如果删除的节点是非叶子节点,则删除该子树
public void delNode(int no) { //思路
/*
* 1. 因为我们的二叉树是单向的,所以我们是判断当前结点的子结点是否需要删除结点,而不能去判断当前这个结点是不是需要删除结点.
2. 如果当前结点的左子结点不为空,并且左子结点 就是要删除结点,就将this.left = null; 并且就返回(结束递归删除)
3. 如果当前结点的右子结点不为空,并且右子结点 就是要删除结点,就将this.right= null ;并且就返回(结束递归删除)
4. 如果第2和第3步没有删除结点,那么我们就需要向左子树进行递归删除
5. 如果第4步也没有删除结点,则应当向右子树进行递归删除. */
//2. 如果当前结点的左子结点不为空,并且左子结点 就是要删除结点,就将this.left = null; 并且就返回(结束递归删除)
if(this.left != null && this.left.no == no) {
this.left = null;
return;
}
//3.如果当前结点的右子结点不为空,并且右子结点 就是要删除结点,就将this.right= null ;并且就返回(结束递归删除)
if(this.right != null && this.right.no == no) {
this.right = null;
return;
}
//4.我们就需要向左子树进行递归删除
if(this.left != null) {
this.left.delNode(no);
}
//5.则应当向右子树进行递归删除
if(this.right != null) {
this.right.delNode(no);
}
}
}
代码
测试:
public static void main(String[] args) {
//先需要创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
//创建需要的结点
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
HeroNode node5 = new HeroNode(5, "关胜");
//说明,我们先手动创建该二叉树,后面我们学习递归的方式创建二叉树
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
System.out.println("删除前,前序遍历");
binaryTree.preOrder(); // 1,2,3,5,4
binaryTree.delNode(5);
//binaryTree.delNode(3);
System.out.println("删除后,前序遍历");
binaryTree.preOrder(); // 1,2,3,4
}
输出:
删除前,前序遍历
HeroNode [no=1, name=宋江]
HeroNode [no=2, name=吴用]
HeroNode [no=3, name=卢俊义]
HeroNode [no=5, name=关胜]
HeroNode [no=4, name=林冲]
删除后,前序遍历
HeroNode [no=1, name=宋江]
HeroNode [no=2, name=吴用]
HeroNode [no=3, name=卢俊义]
HeroNode [no=4, name=林冲]
如果是删除binaryTree.delNode(3);
则输出:
删除前,前序遍历
HeroNode [no=1, name=宋江]
HeroNode [no=2, name=吴用]
HeroNode [no=3, name=卢俊义]
HeroNode [no=5, name=关胜]
HeroNode [no=4, name=林冲]
删除后,前序遍历
HeroNode [no=1, name=宋江]
HeroNode [no=2, name=吴用]
代码
拓展:
上面我们定义了两个删除规则,那么我们考虑另外删除规则又怎么实现。‘
如果要删除的节点是非叶子节点,现在我们不希望将该非叶子节点为根节点的子树删除,需要指定规则, 假如规定如下:
- 如果该非叶子节点A只有一个子节点B,则子节点B替代节点A
- 如果该非叶子节点A有左子节点B和右子节点C,则让左子节点B替代节点A。
这个代码实现在后续讲二叉排序树时,在讲解具体的删除方法。
顺序存储二叉树
顺序存储二叉树的概念
基本说明
从数据存储来看,数组存储方式和树 的存储方式可以相互转换,即数组可 以转换成树,树也可以转换成数组, 看示意图。
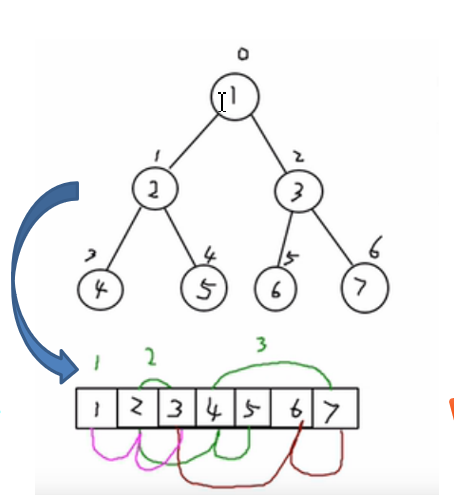
要求:
- 上图的二叉树的结点,要求以数组的方式来存放 arr : [1, 2, 3, 4, 5, 6, 7]
- 要求在遍历数组 arr时,仍然可以以前序遍历,中序遍历和后序遍历的方式完成结点的遍历
顺序存储二叉树的特点:
- 顺序二叉树通常只考虑完全二叉树
- 第n个元素的左子节点为 2 * n + 1
- 第n个元素的右子节点为 2 * n + 2
- 第n个元素的父节点为 (n-1) / 2
- n : 表示二叉树中的第几个元素
需求: 给你一个数组 {1,2,3,4,5,6,7},要求以二叉树前序遍历的方式进行遍历。 前序遍历的结果应当为 1,2,4,5,3,6,7
public class ArrBinaryTreeDemo {
public static void main(String[] args) {
int[] arr = { 1, 2, 3, 4, 5, 6, 7 };
//创建一个 ArrBinaryTree
ArrBinaryTree arrBinaryTree = new ArrBinaryTree(arr);
arrBinaryTree.preOrder(); // 1,2,4,5,3,6,7
}
}
//编写一个ArrayBinaryTree, 实现顺序存储二叉树遍历
class ArrBinaryTree {
private int[] arr;//存储数据结点的数组
public ArrBinaryTree(int[] arr) {
this.arr = arr;
}
//重载preOrder
public void preOrder() {
this.preOrder(0);
}
//编写一个方法,完成顺序存储二叉树的前序遍历
/**
*
* @param index 数组的下标
*/
public void preOrder(int index) {
//如果数组为空,或者 arr.length = 0
if(arr == null || arr.length == 0) {
System.out.println("数组为空,不能按照二叉树的前序遍历");
}
//输出当前这个元素
System.out.println(arr[index]);
//向左递归遍历
if((index * 2 + 1) < arr.length) {
preOrder(2 * index + 1 );
}
//向右递归遍历
if((index * 2 + 2) < arr.length) {
preOrder(2 * index + 2);
}
}
}
代码
顺序存储二叉树应用实例
八大排序算法中的堆排序,就会使用到顺序存储二叉树, 关于堆排序后续在讲。
数据结构与算法---树结构(Tree structure)的更多相关文章
- 【算法】273-每周一练 之 数据结构与算法(Tree)
这是第六周的练习题,最近加班比较多. 下面是之前分享的链接: [算法]200-每周一练 之 数据结构与算法(Stack) [算法]213-每周一练 之 数据结构与算法(LinkedList) [算法] ...
- 每周一练 之 数据结构与算法(Tree)
这是第六周的练习题,最近加班比较多,上周主要完成一篇 GraphQL入门教程 ,有兴趣的小伙伴可以看下哈. 下面是之前分享的链接: 1.每周一练 之 数据结构与算法(Stack) 2.每周一练 之 数 ...
- Python - 数据结构与算法(Data Structure and Algorithms)
入门 The Algorithms Python https://github.com/TheAlgorithms/Python 从基本原理到代码实现的Python算法入门,简洁地展示问题怎样解决,因 ...
- 数据结构与算法--树(tree)结构
树 二叉树 遍历原则:前序遍历是根左右, 中序遍历是左根右,后序遍历是左右根. 二叉搜索树 特点:对于树中的每个节点X,它的左子树中所有节点的值都小于X,右子树中所有节点的值都大于X. 遍历:采取二叉 ...
- [数据结构]——二叉树(Binary Tree)、二叉搜索树(Binary Search Tree)及其衍生算法
二叉树(Binary Tree)是最简单的树形数据结构,然而却十分精妙.其衍生出各种算法,以致于占据了数据结构的半壁江山.STL中大名顶顶的关联容器--集合(set).映射(map)便是使用二叉树实现 ...
- Java数据结构和算法(二)顺序存储的树结构
Java数据结构和算法(二)顺序存储的树结构 数据结构与算法目录(https://www.cnblogs.com/binarylei/p/10115867.html) 二叉树也可以用数组存储,可以和完 ...
- Java数据结构和算法(三)顺序存储的树结构
Java数据结构和算法(三)顺序存储的树结构 二叉树也可以用数组存储,可以和完全二叉树的节点一一对应. 一.树的遍历 // 二叉树保存在数组中 int[] data; public void preO ...
- Pascal数据结构与算法
第一章 数据结构与算法的引入 1.1 数据结构的基本概念 一. 学习数据结构的意义 程序设计 = 数据结构 + 算法 目前,80%的待处理的数据具有“算法简单”(四则运算.检索.排序等),“对象复杂” ...
- Java 内功修炼 之 数据结构与算法(一)
一.基本认识 1.数据结构与算法的关系? (1)数据结构(data structure): 数据结构指的是 数据与数据 之间的结构关系.比如:数组.队列.哈希.树 等结构. (2)算法: 算法指的是 ...
随机推荐
- linq to entity DistinctBy && DefaultIfEmpty
根据某属性去重 使用第三方库: https://github.com/morelinq/MoreLINQ Install-Package morelinq -Version 3.0.0 data.Di ...
- AY写给国人的教程- VS2017 Live Unit Testing[2/2]-C#人爱学不学-aaronyang技术分享
原文:AY写给国人的教程- VS2017 Live Unit Testing[2/2]-C#人爱学不学-aaronyang技术分享 谢谢大家观看-AY的 VS2017推广系列 Live Unit Te ...
- Delphi多线程下的ADO编程
前言: 几个月前接到一个任务:将一后台程序访问数据库的方式从BDE改为ADO,原因是由于业务量的增加,通过BDE不论是向数据库写入数据还是从数据库中读出数据的速度都变得无法忍受,大家都知道ADO在数据 ...
- PHP提取字符串中的图片地址
PHP提取字符串中的图片地址 $str='<p><img border="0" src="upfiles/2009/07/1246430143_1.jp ...
- linux虚拟机上svn客户端连接问题
在虚拟机上搭建好的svn,本地连接居然不行,原来是防火墙端口没开造成的. 修改配置文件:vi /etc/sysconfig/iptables # Generated by iptables-save ...
- 让用户使用第三方账号(如亚马逊账号)接入AWS IoT系统
我们想象这么一个IoT应用场景:厂商A使用AWS IoT来开发物联网解决方案,那么A把设备卖给用户的时候,需要使用户能够登入AWS IoT系统来控制其购买的A的设备,也就是说给用户分配适当的权限.下面 ...
- Win8Metro(C#)数字图像处理--2.11图像锐化
原文:Win8Metro(C#)数字图像处理--2.11图像锐化 [函数名称] 图像锐化函数SharpeningProcess(WriteableBitmap src,double sharpe ...
- SynchronizationContext笔记
SynchronizationContext 类是一个基类,可提供不带同步的自由线程上下文. 此类实现的同步模型的目的是使公共语言运行库内部的异步/同步操作能够针对不同的异步模型采取正确的行为.此模型 ...
- 压缩大文件时如何限制CPU使用率?----几种CPU资源限制方法的测试说明
一.说明 我们的MySQL实例在备份后需要将数据打包压缩,部分低配机器在压缩时容易出现CPU打满导致报警的情况,需要在压缩文件时进行CPU资源的限制. 因此针对此问题进行了相关测试,就有了此文章. 二 ...
- JS解析Json 数据并跳转到一个新页面,取消A 标签跳转
JS解析Json 数据并跳转到一个新页面,代码如下 $.getJSON("http://api.cn.abb.com/common/api/staff/employee/" + o ...
