BFS（三）：双向广度优先搜索

所谓双向广度搜索指的是搜索沿两个方向同时进行：（1）正向搜索：从初始结点向目标结点方向搜索；（2）逆向搜索：从目标结点向初始结点方向搜索；当两个方向的搜索生成同一子结点时终止此搜索过程。

广度双向搜索通常有两种方法：（1）两个方向交替扩展；（2）选择结点个数较少的那个方向先扩展。方法（2）克服了两方向结点的生成速度不平衡的状态，可明显提高效率。

【例1】Knight Moves （POJ 1915）

Description

Background
Mr Somurolov, fabulous chess-gamer indeed, asserts that no one else but him can move knights from one position to another so fast. Can you beat him?
The Problem
Your task is to write a program to calculate the minimum number of moves needed for a knight to reach one point from another, so that you have the chance to be faster than Somurolov.
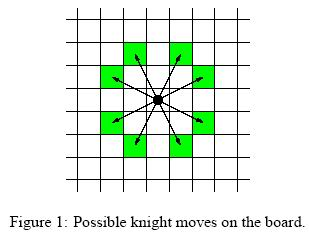
For people not familiar with chess, the possible knight moves are shown in Figure 1.

Input

The input begins with the number n of scenarios on a single line by itself.
Next follow n scenarios. Each scenario consists of three lines containing integer numbers. The first line specifies the length l of a side of the chess board (4 <= l <= 300). The entire board has size l * l. The second and third line contain pair of integers {0, ..., l-1}*{0, ..., l-1} specifying the starting and ending position of the knight on the board. The integers are separated by a single blank. You can assume that the positions are valid positions on the chess board of that scenario.
Output

For each scenario of the input you have to calculate the minimal amount of knight moves which are necessary to move from the starting point to the ending point. If starting point and ending point are equal,distance is zero. The distance must be written on a single line.
Sample Input

3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1
Sample Output

5
28
0

（1）编程思路1。

先采用一般的单向广度优先搜索方法。设置数组step[305][305]记录走到某个位置需要的步数，数组vis[305][305]来记录某个位置是否已访问过（值0代表未访问，1代表已访问过）。

用数组q[]来模拟队列，front和rear分别为队头和队尾指针。单向广度优先搜索的框架可写为：

队列初始化，即front=rear=0;

起点坐标入队列;

while (front<rear)      // 队列不为空

{

队头元素出队，送cur结点；

若cur结点的坐标等于终点坐标，则搜索完成，返回；

将cur结点按规则展出新结点next（即用循环进行8个方向的新结点生成）；

若next结点未访问过，则置相应的值，并将next结点入队；

}

（2）采用单向广度优先搜索的源程序。

#include <stdio.h>

int vis[305][305], step[305][305];

int dx[] = {-2, -2, -1, 1, 2, 2, 1, -1};

int dy[] = {-1, 1, 2, 2, 1, -1, -2, -2};

struct point

{

int x, y;

};

int BFS(int start_x,int start_y,int end_x,int end_y,int n)

// 在n*n的棋盘中搜索从起点（start_x,strat_y)到终点（end_x,end_y)所需的最少步数

{

int front,rear,i;

point cur,next,q[90005];

front=rear=0;

cur.x = start_x;

cur.y = start_y;

vis[start_x][start_y] = 1;   // 设置探索标记为1

q[rear++] = cur;              // 起始坐标入队

while (front < rear)

{

cur = q[front++];       // 队头结点坐标出队

for (i=0; i<8; ++i)

{

next.x = cur.x + dx[i];

next.y = cur.y + dy[i];

if (next.x<0 || next.x>=n || next.y<0 || next.y>=n)

continue;

if (next.x==end_x && next.y==end_y)   // 到达目标位置

return step[cur.x][cur.y]+1;

if (!vis[next.x][next.y])

{

vis[next.x][next.y] = 1;

step[next.x][next.y] = step[cur.x][cur.y] + 1; // 记录步数

q[rear++] = next; // 当前合法坐标位置入队

}

}

}

return -1;  // 若搜索不成功，表示不可达

}

int main()

{

int nCase,sx,sy,tx,ty,size,i,j;

scanf("%d", &nCase);

while (nCase--)

{

scanf("%d", &size);

for (i=0;i<size;i++)

for (j=0;j<size;j++)

vis[i][j]=step[i][j]=0;

scanf("%d %d", &sx, &sy);

scanf("%d %d", &tx, &ty);

if (sx==tx && sy==ty)

{

printf("0\n");

}

else

{

printf("%d\n",BFS(sx,sy,tx,ty,size));

}

}

return 0;

}

（3）编程思路2。

用同一个队列来保存正向和逆向扩展的结点。开始时，将起点坐标和终点坐标同时入队列。这样，第1个出队的坐标是起点，正向搜索扩展队列；第2个出队的坐标是终点，逆向搜索扩展队列。…，两个方向的扩展依次交替进行。

由于采用双向搜索，如何知道某个结点是正向还是逆向扩展来的呢？

简单修改vis[][]数组元素的置值方法即可。初始时，vis数组的全部元素值为0，由正向扩展来的结点的vis对应元素值置为1，由逆向扩展来的结点的vis对应元素值置为2。

设当前结点为cur，由cur可以扩展出新结点next。若vis[next.x][next.y]==0，则next结点未访问过，将next结点入队并进行相应设置；若vis[next.x][next.y]！=0，则next结点已访问过。由于vis[cur.x][cur.y]记录的是当前扩展方向（1代表正向，2代表逆向），若vis[next.x][next.y] != vis[cur.x][cur.y]，则表示next结点以前按相反的方向访问过，正向和反向遇到了同一个结点，搜索成功。

（4）采用双向广度优先搜索的源程序。

#include <stdio.h>

int vis[305][305], step[305][305];

int dx[] = {-2, -2, -1, 1, 2, 2, 1, -1};

int dy[] = {-1, 1, 2, 2, 1, -1, -2, -2};

struct point

{

int x, y;

};

int BFS(int start_x,int start_y,int end_x,int end_y,int n)

// 在n*n的棋盘中搜索从起点（start_x,strat_y)到终点（end_x,end_y)所需的最少步数

{

int front,rear,i;

point cur,next,q[90005];

front=rear=0;

cur.x = start_x;

cur.y = start_y;

vis[start_x][start_y] = 1;  // 从起始位置开始的探索标记为1

q[rear++] = cur;         // 起始坐标入队

next.x = end_x;

next.y = end_y;

vis[end_x][end_y] = 2;   // 从终点位置开始的探索标记为 2

q[rear++] = next;    // 终点坐标入队

while (front < rear)

{

cur = q[front++];     /* 队首结点坐标出队 */

for (i=0; i<8; ++i)

{

next.x = cur.x + dx[i];

next.y = cur.y + dy[i];

if (next.x<0 || next.x>=n || next.y<0 || next.y>=n)

continue;

if (!vis[next.x][next.y])

{

vis[next.x][next.y] = vis[cur.x][cur.y];     // 设为与当前探索路径相同的标记

step[next.x][next.y] = step[cur.x][cur.y] + 1; // 记录步数

q[rear++] = next; // 当前合法坐标位置入队

}

else if (vis[cur.x][cur.y] != vis[next.x][next.y])

{   // 说明从起点出发的探索与从终点出发的探索重合

return step[cur.x][cur.y]+step[next.x][next.y]+1;

}

}

}

return -1;  // 若搜索不成功，表示不可达

}

int main()

{

int nCase,sx,sy,tx,ty,size,i,j;

scanf("%d", &nCase);

while (nCase--)

{

scanf("%d", &size);

for (i=0;i<size;i++)

for (j=0;j<size;j++)

vis[i][j]=step[i][j]=0;

scanf("%d %d", &sx, &sy);

scanf("%d %d", &tx, &ty);

if (sx==tx && sy==ty)

{

printf("0\n");

}

else

{

printf("%d\n",BFS(sx,sy,tx,ty,size));

}

}

return 0;

}

（5）编程思路3。

定义两个队列q1[]和q2[]分别用于两个方向的扩展，两个队列的队头指针和队尾指针分别为front1、front2和rear1、rear2。双向广度优先搜索的框架还可写成：
      void BFS()
      {

将起始节点放入队列q1，将目的节点放入队列q2；

当两个队列都未空时，作如下循环
           {
                 如果队列q1里的未处理节点比q2中的少（即rear1-front1 < rear2-front2)，

则扩展队列q1；

否则扩展队列q2；
             }

}

（6）采用两个队列的双向广度优先搜索方法的源程序。

#include <stdio.h>

int vis[305][305], step[305][305];

int dx[] = {-2, -2, -1, 1, 2, 2, 1, -1};

int dy[] = {-1, 1, 2, 2, 1, -1, -2, -2};

struct point

{

int x, y;

};

int BFS(int start_x,int start_y,int end_x,int end_y,int n)

// 在n*n的棋盘中搜索从起点（start_x,strat_y)到终点（end_x,end_y)所需的最少步数

{

int front1,rear1,front2,rear2,i,flag;

point cur,next,q1[45001],q2[45001];

front1=rear1=0;

front2=rear2=0;

cur.x = start_x;

cur.y = start_y;

vis[start_x][start_y] = 1;  // 设置正向探索标记为1

q1[rear1++] = cur;           // 起始坐标入正向队列

next.x = end_x;

next.y = end_y;

vis[end_x][end_y] = 2;      // 设置逆向探索标记为2

q2[rear2++] = next;          // 终点坐标入逆向队列

while (front1 < rear1 && front2<rear2)

{

if (rear1-front1 < rear2-front2)

{

cur = q1[front1++]; flag=1;    // 扩展正向队列

}

else

{

cur = q2[front2++]; flag=2;    // 扩展逆向队列

}

for (i=0; i<8; ++i)

{

next.x = cur.x + dx[i];

next.y = cur.y + dy[i];

if (next.x<0 || next.x>=n || next.y<0 || next.y>=n)

continue;

if (!vis[next.x][next.y])

{

vis[next.x][next.y] = flag;

step[next.x][next.y] = step[cur.x][cur.y] + 1;

if (flag==1)

q1[rear1++] = next;

else

q2[rear2++] = next;

}

else if (vis[cur.x][cur.y] != vis[next.x][next.y])

{

return step[cur.x][cur.y]+step[next.x][next.y]+1;

}

}

}

return -1;  // 若搜索不成功，表示不可达

}

int main()

{

int nCase,sx,sy,tx,ty,size,i,j;

scanf("%d", &nCase);

while (nCase--)

{

scanf("%d", &size);

for (i=0;i<size;i++)

for (j=0;j<size;j++)

vis[i][j]=step[i][j]=0;

scanf("%d %d", &sx, &sy);

scanf("%d %d", &tx, &ty);

if (sx==tx && sy==ty)

{

printf("0\n");

}

else

{

printf("%d\n",BFS(sx,sy,tx,ty,size));

}

}

return 0;

}