[BZOJ1965][AHOI2005] 洗牌 - 扩展欧几里得

题目描述

为了表彰小联为Samuel星球的探险所做出的贡献，小联被邀请参加Samuel星球近距离载人探险活动。

由于Samuel星球相当遥远，科学家们要在飞船中度过相当长的一段时间，小联提议用扑克牌打发长途旅行中的无聊时间。玩了几局之后，大家觉得单纯玩扑克牌对于像他们这样的高智商人才来说太简单了。有人提出了扑克牌的一种新的玩法。

对于扑克牌的一次洗牌是这样定义的，将一叠N（N为偶数）张扑克牌平均分成上下两叠，取下面一叠的第一张作为新的一叠的第一张，然后取上面一叠的第一张作为新的一叠的第二张，再取下面一叠的第二张作为新的一叠的第三张……如此交替直到所有的牌取完。

如果对一叠6张的扑克牌1 2 3 4 5 6，进行一次洗牌的过程如下图所示：

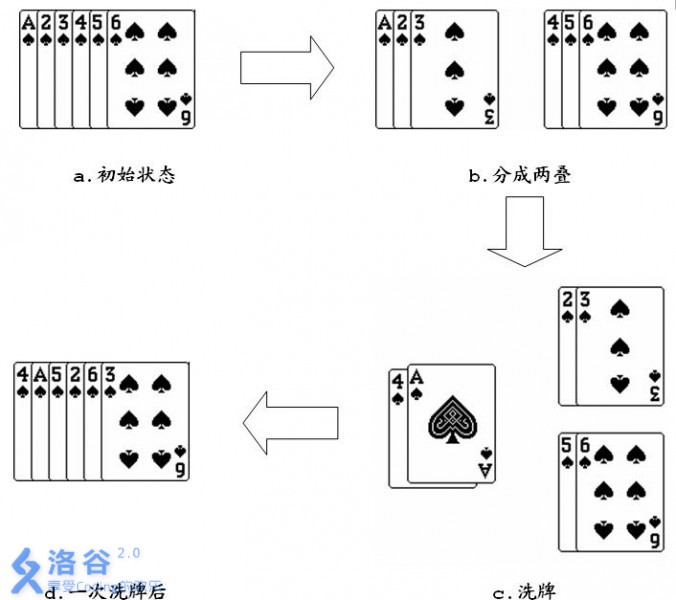
从图中可以看出经过一次洗牌，序列1 2 3 4 5 6变为4 1 5 2 6 3。当然，再对得到的序列进行一次洗牌，又会变为2 4 6 1 3 5。

游戏是这样的，如果给定长度为N的一叠扑克牌，并且牌面大小从1开始连续增加到N（不考虑花色），对这样的一叠扑克牌，进行M次洗牌。最先说出经过洗牌后的扑克牌序列中第L张扑克牌的牌面大小是多少的科学家得胜。小联想赢取游戏的胜利，你能帮助他吗？

输入输出格式

输入格式：

输入文件中有三个用空格间隔的整数，分别表示N，M，L

（其中0＜N≤10^10 ，0 ≤M≤10^10，且N为偶数）。

输出格式：

单行输出指定的扑克牌的牌面大小。

输入输出样例

输入样例#1：

6 2 3

输出样例#1：

6

说明

0＜N≤10^10 ，0 ≤M≤10^10，且N为偶数

---

题解：

打表并没有发现规律于是决定手推一波公式；

x -> x * 2(x <= n/2)

x -> x * 2 - n - 1(x > n/2)

仔细看看...发现改变后的位置是(x*2)mod(n+1）

于是..x*2^m ≡ L mod (n + 1) ,x是我们要求的位置

于是扩展欧几里得就解决了..

---

Code：

#include <iostream>
#include <cstdio>
using namespace std;
#define ll long long
ll n, m, L;
inline ll ksm(ll x, ll y)
{
    ll res = ;
    while(y){if(y&)res=res*x%(n+);x=x*x%(n+);y>>=;}
    return res;
}
inline ll gcd(ll a, ll b){return b==?a:gcd(b,a%b);}
inline void exgcd(ll a, ll b, ll &x, ll &y)
{
    if (b==) {x=,y=;return;}
    exgcd(b,a%b,x,y);
    ll t = x;
    x = y;
    y = t - a / b * y;
}

int main()
{
    scanf("%lld%lld%lld",&n,&m,&L);
    ll A = ksm(, m), B = n + , C = L ;
    ll g = gcd(A, B);
    A /= g, B /= g, C /= g;
    ll x, y;
    exgcd(A, B, x, y);
    ll ans = ((x * C) % B + B) % B;
    cout << ans ;
    return ;
}