NOIP模拟测试6
看题目就知道这是一个悲伤的故事。。。
但还有更悲伤的
考崩了，难以描述。
T1把数据范围看成2^12,我TM也是够了。。。
T2思路接近正解，但不知道想了个神魔东西跑了N遍dijstra
T3最狗了，暴力二十分没拿到，因为我打的贪心。。
T1：很水的DP+组合数学
DP转移显然：f[i][j]=sum[i-1][j-1]-sum[i-1][j-m];但是这样时空复杂度都是（N*d）但期望复杂度是（N^2）考虑如何优化发现f[i][j]实际上有许多零出现，但我们还把它当成有用的状态转移了，因此考虑抹去这些冗余。用组合数学，f[i][j]的定义改为送出礼物的i天 注意取模！
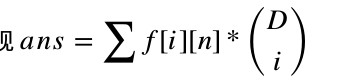AC代码：
#include<bits/stdc++.h>
#define MAXN 2005
#define mem(a) memset(a,0,sizeof(a))
using namespace std;
const long long mod=;
long long C[MAXN],inv[MAXN];
inline long long Rd()
{
long long x=;char c=getchar();long long f=;
while(c<''||c>''){if(c=='-')f=-;c=getchar();}
while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
return x*f;
}
long long n,d,m;
long long f[MAXN][MAXN],sum[MAXN][MAXN];
inline long long qpower(long long a,long long b)
{
long long ans=;
while(b)
{
if(b&)ans=ans*a%mod;
a=a*a%mod;
b>>=;
}
return ans%mod;
}
inline void Get_C()
{
C[]=d%mod;
for(long long i=;i<=n;i++)
{
C[i]=C[i-]*inv[i]%mod*((d-i+)%mod)%mod;
}
}
int main()
{
//freopen("out.in","r",stdin);
//freopen("a.txt","w",stdout);
for(long long i=;i<=;i++)inv[i]=qpower(i,mod-);
while()
{
mem(sum);mem(f);
n=Rd();d=Rd();m=Rd();
long long ans=;
Get_C();
if(n==&&d==&&m==)return ;
for(long long i=;i<m;i++)f[][i]=,sum[][i]=sum[][i-]+f[][i];
for(long long i=m;i<=n;i++)sum[][i]=sum[][m-];
for(long long i=;i<=n;i++)
{
for(long long j=;j<=n;j++)
{
if(j>=m)f[i][j]=(mod+sum[i-][j-]-sum[i-][j-m])%mod;
else f[i][j]=sum[i-][j-];
sum[i][j]=(sum[i][j-]+f[i][j])%mod;
}
}
for(int i=;i<=n;i++)ans=(ans+C[i]*f[i][n]%mod)%mod;
cout<<ans%mod<<endl;
}
return ;
}
T2：找最小环
想了一个**算法，时间复杂度O（n^2log(n)）空间复杂度（n^2）
#include<cstdio>
#include<queue>
#include<bits/stdc++.h>
#define ts puts("---------------");
#define MAXN 20005
#define mem(a) memset(a,0,sizeof(a))
using namespace std;
int head[MAXN],nxt[MAXN],to[MAXN],cnt,s[MAXN],top,dfn[MAXN],low[MAXN],ans,tot,v[MAXN],val[MAXN];
bool yes_get,vst[],in_s[MAXN],Fail[MAXN*];
int edge[][],d[],di[],pre[];
void clear()
{
mem(head);mem(s);mem(dfn);mem(in_s);mem(v);mem(Fail);mem(vst);mem(pre);
yes_get=ans=tot=cnt=top=;
}
inline int Rd()
{
int x=;char c=getchar();int f=;
while(c<''||c>''){if(c=='-')f=-;c=getchar();}
while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
return x*f;
}
void add(int u,int v,int w)
{
to[++cnt]=v;
nxt[cnt]=head[u];
val[cnt]=w;
head[u]=cnt;
return ;
}
void Tarjan(int x,int fa)
{
dfn[x]=low[x]=++tot;
s[++top]=x;
in_s[x]=;
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(y==fa)continue;
if(!dfn[y])
{
v[y]=val[i];
Tarjan(y,x);
low[x]=min(low[x],low[y]);
}
else
{
if(in_s[y])
{
if(dfn[y]<low[x])v[x]+=val[i];
low[x]=min(low[x],dfn[y]);
}
}
} if(low[x]==dfn[x])
{
ans=;
while(top)
{
int p=s[top--];
in_s[p]=;
ans+=v[p];
if(p==)yes_get=;
if(p==x)break;
}
}
if(!yes_get||!ans)ans=-;
else return ;
}
int Getmin(int i)
{
priority_queue<pair<int,int> >Q;
while(Q.size())Q.pop();
memset(di,0x3f,sizeof(di));
mem(vst);
di[]=;
Q.push(make_pair(,));
while(!Q.empty())
{
pair<int,int>k=Q.top();Q.pop();
int x=k.second;
if(vst[x])continue;
if(x==i)return di[x];
vst[x]=;
for(int i=head[x];i;i=nxt[i])
{
if(Fail[i])continue;
int y=to[i],va=val[i];
if(va+di[x]<di[y])
{
di[y]=va+di[x];
Q.push(make_pair(-di[y],y));
}
}
}
return di[];
}
void pre_Get()
{
priority_queue<pair<int,int> >Q;
memset(d,0x3f,sizeof(d));
mem(vst);
d[]=;
Q.push(make_pair(,));
while(!Q.empty())
{
pair<int,int>k=Q.top();Q.pop();
int x=k.second;
if(vst[x])continue;
vst[x]=;
for(int i=head[x];i;i=nxt[i])
{
int y=to[i],va=val[i];
if(va+d[x]<d[y])
{
pre[y]=x;
d[y]=va+d[x];
Q.push(make_pair(-d[y],y));
}
}
}
return ;
}
int main()
{
// freopen("out.in","r",stdin);
// freopen("b.txt","w",stdout);
int t=Rd();
while(t--)
{
clear();
int n=Rd(),m=Rd();
if(n==m)
{
while(m--)
{
int u=Rd(),v=Rd(),w=Rd();
add(u,v,w);
add(v,u,w);
}
Tarjan(,);
cout<<ans<<endl;
}
else
{
ans=0x7f7f7f7f;
while(m--)
{
int u=Rd(),v=Rd(),w=Rd();
add(u,v,w);
edge[u][v]=cnt;
add(v,u,w);
edge[v][u]=cnt;
}
pre_Get();
for(int i=;i<=n;i++)
{
if(d[i]==d[])continue;
int t=i;
while(t!=&&t!=)
{
Fail[edge[pre[t]][t]]=;
Fail[edge[t][pre[t]]]=;
t=pre[t];
}
if(Getmin(i)!=di[])ans=min(ans,Getmin(i)+d[i]);
t=i;
while(t!=)
{
Fail[edge[pre[t]][t]]=;
Fail[edge[t][pre[t]]]=;
t=pre[t];
}
}
cout<<(ans==0x7f7f7f7f?-:ans)<<endl;
}
}
return ;
}
/*
1
4 5
1 2 2
2 3 2
3 4 2
1 4 2
1 3 5
*/
献出我的sb算法
但实际上仔细想想发现，我的算法是有许多冗余的，只需要枚举和一直接相邻的边就够了。
因此。。。
AC代码
#include<cstdio>
#include<queue>
#include<bits/stdc++.h>
#define ts puts("---------------");
#define MAXN 80005
#define mem(a) memset(a,0,sizeof(a))
using namespace std;
int head[MAXN],nxt[MAXN],to[MAXN],cnt=,ans,val[MAXN];
bool Fail[MAXN],vst[];
int di[];
void clear()
{
mem(head);mem(Fail);
cnt=;
}
inline int Rd()
{
int x=;char c=getchar();int f=;
while(c<''||c>''){if(c=='-')f=-;c=getchar();}
while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
return x*f;
}
void add(int u,int v,int w)
{
to[++cnt]=v;
nxt[cnt]=head[u];
val[cnt]=w;
head[u]=cnt;
return ;
}
int Getmin(int i,int ww)
{
priority_queue<pair<int,int> >Q;
while(Q.size())Q.pop();
memset(di,0x3f,sizeof(di));
mem(vst);
di[]=;
Q.push(make_pair(,));
while(!Q.empty())
{
pair<int,int>k=Q.top();Q.pop();
int x=k.second;
if(di[x]+ww>ans)return di[x]+ww;
if(vst[x])continue;
if(x==i)return di[x]+ww;
vst[x]=;
for(int i=head[x];i;i=nxt[i])
{
if(Fail[i])continue;
int y=to[i],va=val[i];
if(va+di[x]<di[y])
{
di[y]=va+di[x];
Q.push(make_pair(-di[y],y));
}
}
}
return di[];
}
int main()
{
// freopen("out.in","r",stdin);
// freopen("b.txt","w",stdout);
int t=Rd();
while(t--)
{
clear();
int n=Rd(),m=Rd();
ans=0x3f3f3f3f;
while(m--)
{
int u=Rd(),v=Rd(),w=Rd();
add(u,v,w);
add(v,u,w);
}
for(int i=head[];i;i=nxt[i])
{
int k=to[i];
Fail[i]=Fail[i^]=;
ans=min(ans,Getmin(k,val[i]));
Fail[i]=Fail[i^]=;
}
cout<<(ans==0x3f3f3f3f?-:ans)<<endl;
}
return ;
}
/*
1
4 5
1 2 2
2 3 2
3 4 2
1 4 2
1 3 5
*/
LNC的A*算法（借鉴一下，无意侵权）
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
const int maxn=1e4+,maxm=4e4+,INF=0x3f3f3f3f;
int T,n,m,x,y,z,dex,yes,tot=,top,cld[maxn],yet[maxn],instack[maxn],stack[maxn],first[maxn];
struct road{
int u,t,w,nxt;
}eage[maxm<<];
struct point1{
int id,dis;
bool friend operator < (const point1 a,const point1 b)
{
return a.dis>b.dis;
}
}dis[maxn];
struct point2{
int id,h;
bool friend operator < (const point2 a,const point2 b)
{
return dis[a.id].dis+a.h>dis[b.id].dis+b.h;
}
};
priority_queue<point1> q1;
priority_queue<point2> q2;
void add(int x,int y,int z)
{
eage[++tot].u=x;
eage[tot].t=y;
eage[tot].w=z;
eage[tot].nxt=first[x];
first[x]=tot;
}
void clear()
{
top=;tot=;
memset(first,,sizeof(first));
memset(cld,,sizeof(cld));
memset(yet,,sizeof(yet));
memset(instack,,sizeof(instack));
}
void dijk()
{
memset(yet,,sizeof(yet));
for(int i=;i<=n;i++) dis[i].id=i,dis[i].dis=INF;
dis[].dis=;
q1.push(dis[]);
while(q1.empty()==)
{
int x=q1.top().id;q1.pop();
if(yet[x]) continue;
yet[x]=;
for(int i=first[x];i;i=eage[i].nxt)
if(dis[x].dis+eage[i].w<dis[eage[i].t].dis)
dis[eage[i].t].dis=dis[x].dis+eage[i].w,q1.push(dis[eage[i].t]);
}
memset(yet,,sizeof(yet));
}
int work(int st)
{
while(q2.empty()==) q2.pop();
point2 x,tmp;
x.id=st;x.h=;
q2.push(x);
int ans=INF;
while(q2.empty()==)
{
x=q2.top();q2.pop();
yet[x.id]=;
if(x.id==)
{
ans=x.h;
break;
}
for(int i=first[x.id];i;i=eage[i].nxt)
if(i!=dex&&yet[eage[i].t]==)
{
tmp.id=eage[i].t;
tmp.h=eage[i].w+x.h;
q2.push(tmp);
}
}
memset(yet,,sizeof(yet));
return ans;
}
void Astar()
{
dijk();
int ans=INF;
for(int i=first[];i;i=eage[i].nxt)
{
dex=i^;
int t=eage[i].t,d=work(t)+eage[i].w;
ans=min(d,ans);
}
printf("%d\n",ans>?-:ans);
return ;
}
int main()
{
scanf("%d",&T);
while(T--)
{
scanf("%d%d",&n,&m);
while(m--)
{
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);add(y,x,z);
}
Astar();
clear();
}
}
T3：又是一道足以把评测机卡崩的题 好题标记
毫无头绪？
是的 毫无头绪是真的毫无头绪，但根据数据范围可以推测复杂度应该接近O（n）（T=50，5000ms限制啧啧啧）
就此展开，感觉dp否了，递推。。。也不大可能，所以我们自然会想到搜索图论，（好吧我承认有点牵强，但说实话，O(n)的算法真的不多，这总不能单队维护吧QwQ）
然后就会有奇妙的发现：如果两两连边HiaHiaHia，没神魔卵用，就会发现其实操作只是把边反过来而已。而题目的目标就是每个点的入度<=1。
既然这样，那就继续探索。把这个图画出来，手玩小样例后发现图被分成了几个连通块，然后就可以分类讨论了：
1.m>n 显然是不对的，因为要保证每条边都指向一个点，每个点又要被不大于一条边指（这这这不可能）。
2.m=n 是棵基环树！！！！先考虑环，环可以顺时针也可以逆时针，所以分两种情况，再看以环为根的子树，不管环咋转，子树永远是外向的，所以一遍dfs即可
3.m<n 要保证图联通所以这一定是棵树，而且是棵外向树，快乐吗？可问题是根是不确定的。
下面引入新概念：
二次扫描和换根法：对于不定根的树状DP，暴力枚举是O(n^2)，但我们可以先考虑一个点，再考虑用已知点更新未知点，即考虑换根的代价。
但只适用于不管换不换根，旧根与新根的共同子树状态不变。（纯属博猪个人理解，如有错误，多谢指正）
好啦，有了这个强大的方法，我们就可以成功AC了
AC 代码：
#include<bits/stdc++.h>
#define mem(a) memset(a,0,sizeof(a))
#define MAXN 200000
using namespace std;
const int mod=;
struct node{
int head[MAXN],to[MAXN],nxt[MAXN],cnt,dfn[MAXN],now_minn,now_tot,v[MAXN];long long tot;
int use,sum,fa[MAXN],d[MAXN],f[MAXN];
long long ans,minn;
bool orz[MAXN],vst[MAXN],inlop[MAXN],vst1[MAXN],vst2[MAXN];
vector<int>lop;
void clear()
{
lop.clear();cnt=;ans=;minn=;tot=;mem(fa);mem(v);
mem(inlop);mem(vst);mem(vst1);mem(vst2);
mem(d);mem(f);
mem(dfn);
mem(head);
}
void add(int u,int v,int opt)
{
to[++cnt]=v;
nxt[cnt]=head[u];
head[u]=cnt;
orz[cnt]=opt;
return ;
}
inline int Rd()
{
int x=;
char c=getchar();
int f=;
while(c<''||c>''){if(c=='-')f=-;c=getchar();}
while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
return x*f;
}
bool Getlop(int x,int edge)
{
dfn[x]=++tot;
for(int i=head[x];i;i=nxt[i])
{
if(i==(edge^))continue;
int y=to[i];
if(dfn[y])
{
if(sum==){sum++;continue;}
if(sum>)return ;
sum++;
inlop[y]=;
lop.push_back(y);
if(orz[i])use=;
else use=;
int p=x;
while(p!=y)
{
lop.push_back(p);
inlop[p]=;
use+=v[p];
p=fa[p];
}
}
else {fa[y]=x,v[y]=orz[i];if(Getlop(y,i)==)return ;}
}
return ;
}
void dp(int x)
{
vst[x]=;
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(vst[y]||inlop[y])continue;
dp(y);
d[x]+=d[y];
if(!orz[i])d[x]++;
}
return ;
}
void dprt(int x)
{
vst2[x]=;
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(vst2[y]||inlop[y])continue;
if(orz[i])f[y]=f[x]+;
else f[y]=f[x]-;
dprt(y);
}
return ;
}
void Getans(int x)
{
vst1[x]=;
if(f[x]==now_minn){now_tot++;}
else if(f[x]<now_minn){now_tot=;now_minn=f[x];}
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(vst1[y]||inlop[y])continue;
Getans(y);
}
return ;
}
void work()
{
clear();
// cout<<tot<<endl;
int n=Rd();
for(int i=;i<=n;i++)
{
int a=Rd(),b=Rd();
add(b,a,);
add(a,b,);
}
for(int i=;i<=*n;i++)
{
if(dfn[i]||!head[i])continue;
lop.clear();sum=;
use=;
bool ok=Getlop(i,);
if(!ok){puts("-1 -1");return ;}
else
{
if(!lop.size())
{
now_minn=0x7f7f7f7f;
now_tot=;dp(i);
f[i]=d[i];
dprt(i);
Getans(i);
minn+=now_minn;
ans=ans*now_tot%mod;
}
else
{
int len=lop.size();
//cout<<len<<" "<<use<<endl;
if(use+use^len)
{
minn+=min(use,len-use);
for(int i=;i<len;i++)
{
now_minn=0x7f7f7f7f;
now_tot=;dp(lop[i]);
now_minn=d[lop[i]];
minn+=now_minn;
}
}
else
{
minn+=use;
ans=ans*%mod;
for(int i=;i<len;i++)
{
now_minn=0x7f7f7f7f;
now_tot=;dp(lop[i]);
now_minn=d[lop[i]];
minn+=now_minn;
}
}
}
}
}
printf("%lld %lld\n",minn,ans);
}
}E;
int main()
{
// freopen("out.in","r",stdin);
// freopen("b.txt","w",stdout);
int t=E.Rd();
while(t--)E.work();
return ;
}
总结：
1.考试审题！囧
2.仔细想想自己的复杂度能不能下降，能不能避免不必要的枚举，哪怕搜索打个剪枝也是好的。
3.暴力别打错了！
4.结合着期望的复杂度去思考问题，相信自己。
下次加油！
NOIP模拟测试6的更多相关文章
- 「题解」NOIP模拟测试题解乱写II（36）
毕竟考得太频繁了于是不可能每次考试都写题解.(我解释个什么劲啊又没有人看) 甚至有的题目都没有改掉.跑过来写题解一方面是总结,另一方面也是放松了. NOIP模拟测试36 T1字符 这题我完全懵逼了.就 ...
- 2019.8.3 [HZOI]NOIP模拟测试12 C. 分组
2019.8.3 [HZOI]NOIP模拟测试12 C. 分组 全场比赛题解:https://pan.baidu.com/s/1eSAMuXk 刚看这题觉得很难,于是数据点分治 k只有1和2两种,分别 ...
- 2019.8.3 [HZOI]NOIP模拟测试12 B. 数颜色
2019.8.3 [HZOI]NOIP模拟测试12 B. 数颜色 全场比赛题解:https://pan.baidu.com/s/1eSAMuXk 数据结构学傻的做法: 对每种颜色开动态开点线段树直接维 ...
- 2019.8.3 [HZOI]NOIP模拟测试12 A. 斐波那契(fibonacci)
2019.8.3 [HZOI]NOIP模拟测试12 A. 斐波那契(fibonacci) 全场比赛题解:https://pan.baidu.com/s/1eSAMuXk 找规律 找两个节点的lca,需 ...
- NOIP模拟测试17&18
NOIP模拟测试17&18 17-T1 给定一个序列,选取其中一个闭区间,使得其中每个元素可以在重新排列后成为一个等比数列的子序列,问区间最长是? 特判比值为1的情况,预处理比值2~1000的 ...
- NOIP模拟测试1(2017081501)
好,今天是cgg第一次举行模拟测试,希望各位支持. 时间限制:2小时 题目链接: 题目一:水得都没名字了 题目二:车站 题目三:选数 不要觉得2小时太少,我的题目很良心,都很简单. 答案可以在模拟测试 ...
- 「题解」NOIP模拟测试题解乱写I（29-31）
NOIP模拟29(B) T1爬山 简单题,赛时找到了$O(1)$查询的规律于是切了. 从倍增LCA那里借鉴了一点东西:先将a.b抬到同一高度,然后再一起往上爬.所用的步数$×2$就是了. 抬升到同一高 ...
- 2019.8.14 NOIP模拟测试21 反思总结
模拟测试20的还没改完先咕着 各种细节问题=错失190pts T1大约三分钟搞出了式子,迅速码完,T2写了一半的时候怕最后被卡评测滚去交了,然后右端点没有初始化为n…但是这样还有80pts,而我后来还 ...
- 2019.8.9 NOIP模拟测试15 反思总结
日常爆炸,考得一次比一次差XD 可能还是被身体拖慢了学习的进度吧,虽然按理来说没有影响.大家听的我也听过,大家学的我也没有缺勤多少次. 那么果然还是能力问题吗……? 虽然不愿意承认,但显然就是这样.对 ...
- 2019.8.1 NOIP模拟测试11 反思总结
延迟了一天来补一个反思总结 急匆匆赶回来考试,我们这边大家的状态都稍微有一点差,不过最后的成绩总体来看好像还不错XD 其实这次拿分的大都是暴力[?],除了某些专注于某道题的人以及远程爆踩我们的某学车神 ...
随机推荐
- 设置Activity全屏的方法：
1)代码隐藏ActionBar 在Activity的onCreate方法中调用getActionBar.hide();即可 2)通过requestWindowFeature设置 requestWind ...
- TensorFlow2.0（六）：Dataset
.caret, .dropup > .btn > .caret { border-top-color: #000 !important; } .label { border: 1px so ...
- 杂谈：开发人员如何进行复杂业务的学习？让boss刮目相看
一点小拙见,欢迎指正 一.概述 大型复杂的软件系统,是有许多人共同协作完成的,有些产品的业务是很复杂的,其在需求文档,及开发规范上都做得很好,不然维护的人越多,没有文档和规范去限制,岂不更加乱套. 如 ...
- python编程基础之三十三
构造方法: 目的:构造方法用于初始化对象,可以在构造方法中添加成员属性 触发时机:实例化对象的时候自动调用 参数:第一个参数必须是self,其它参数根据需要自己定义 返回值:不返回值,或者说返回Non ...
- asp.net mvc select用法
var statusSelectItems = new List<SelectListItem> { "}, "}, "}, "}, "} ...
- .NET北京俱乐部，技术的饕餮盛宴，不枉此行
在19年年尾,我们相约于.NET北京俱乐部 DNT精英论坛暨.NET北京俱乐部是由资深.NET专家和社区活跃分子发起的技术论坛,以“分享.成长.合作.共赢”为原则,致力于打造一个领先的技术分享平台和成 ...
- PHP array_pop
1.函数的作用:删除数组的最后一个元素并返回 2.函数的参数: @params array &$array 3.注意点: 每次调用之后,重置指针 4.例子: <?php $product ...
- java控制执行流程
控制执行流程 欢迎转载,转载烦请注明出处,谢谢. https://www.cnblogs.com/sx-wuyj/p/11177257.html java当中涉及到的关键字包括if-else.whil ...
- c++11::initializer_list
#include <initializer_list> template <class T> class initializer_list; initializer_list对 ...
- HDU 1198 Farm Irrigation(状态压缩+DFS)
题目网址:http://acm.hdu.edu.cn/showproblem.php?pid=1198 题目: Farm Irrigation Time Limit: 2000/1000 MS (Ja ...