机器学习笔记（六） ---- 支持向量机（SVM）

支持向量机（SVM）可以说是一个完全由数学理论和公式进行应用的一种机器学习算法，在小批量数据分类上准确度高、性能好，在二分类问题上有广泛的应用。

同样是二分类算法，支持向量机和逻辑回归有很多相似性，都是二分类问题的判决模型，主要的差异在于损失函数的不同，支持向量机相比于逻辑回归，更倾向于找到样本空间中最优的划分超平面。

首先说一下超平面的概念：超平面是一个数学概念，而不好以物理概念解释，因为画不出来：）。n维空间的超平面表示 Wtx + b = 0。二维空间中，超平面是一条直线，三维空间中，超平面是一个平面，以此类推...

--线性支持向量机

我们先假设数据集是线性可分的，这是使用SVM的前提条件（线性不可分其实也有办法解决，后面再说），什么是线性可分呢？

线性可分：对于二维（两个特征）数据集来说，如果存在一条直线，能把这两类数据完全区分开，就说这个数据集是线性可分的。如果多维（k个特征）数据，存在一个维度为k-1的超平面能完全分开两类数据，也称为线性可分。

SVM要解决的问题：就是在样本空间中找到最优（最鲁棒、泛化能力最强）划分超平面。如下图所示，能把两类点分开来的直线有很多，但哪条是最优的呢，这就是SVM要解决的问题。

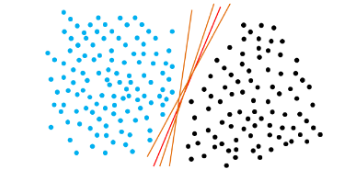
最优超平面有个非常拗口的解释：离超平面最近的特征向量有最大的离超平面的间隔距离。

假设最优超平面为 Wtx + b = f(x)，如下图所示，当f(x)为0的时候，x便是位于超平面上的点，f(x)>0的点对应红色的点，f(x)<0对应蓝色五角星的点，虚线上的点就是距离超平面最近的样本点，也就是“支持向量（Support Vector）”，支持向量机就是要找到距离支持向量距离之和最大的超平面。

两个异类支持向量到超平面距离之和称为“间隔”，间隔的大小计算公式为

SVM的基本模型如下，其中s.t是限制条件，可以理解为在限制条件下，找到满足间隔距离最大的w和b。这就演变成一个带约束的二次规划问题，是一个凸问题，在数学上可以引入拉格朗日函数和对偶变量来求解，这个过程完全是数学推导，非常复杂，感兴趣的可以在网上找资料看看。

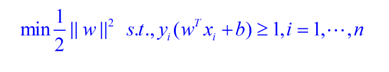
--非线性支持向量机

相比较线性可分，另一种情况就是非线性可分，如下图，二维空间中，两类数据点无法通过一条直线分开，这时候可以考虑将原始空间映射到一个更高维度的特征空间，使得样本在这个高维特征空间内线性可分。例如把下列二维数据点映射到三维空间后，就能找到一个平面将两类点完美划分开。

用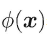

表示映射后的特征向量，则在高维空间中的超平面模型可表示为：

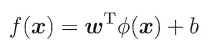
这里ϕ是低维空间到高维空间的映射，这里面有两层含义：

（1）首先使用一个非线性映射将样本空间变换到一个高维特征空间；

（2）再在高维特征空间中使用线性分类器进行分类。

但这样就会出现一个问题，如果凡是遇到线性不可分的情况就映射到高维空间，那有可能维度加得非常多，才能进行线性划分，这样带来的计算复杂度太高，引入“核函数”就是为了解决这个问题。
核函数：假设ϕ是一个从低维空间χ  到高维空间H的映射，存在如下函数，就称为核函数。表示两个原始数据x，z在低维空间中的内积（主要用来衡量两个向量的相似度）。

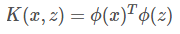
核函数的作用在于：在低维度上进行内积计算，但把实质的分类效果表现在了高维度上，大大降低了计算的复杂度。

      什么样的函数才能充当核函数呢：只要一个对称函数所对应的核矩阵半正定，那它就能作为核函数。这是个很复杂的数学问题，就不展开了，常用的核函数包括线性核函数、多项式核函数、高斯核函数、Sigmoid核函数在各种机器学习框架中都是现成的，可以直接拿来用。

-- 软间隔支持向量机     

在现实问题中，哪怕是用到了核函数，在高维空间中对样本也可能不能线性划分，这就引入了”软间隔支持向量机“。在这种情况下，我们需要允许一些数据点不满足约束条件，即可以在一定程度上偏移超平面，但同时要使得不满足约束条件的数据点尽可能少。如下图，黑圈圈起来的蓝色点就是一个不满足约束条件的点。核心思想就是允许在极少部分样本上出错，但能减低计算复杂度得到一个不过拟合的SVM模型。

软间隔支持向量机的模型可以表示为，相比硬间隔支持向量机，多了一个惩罚项，也可以把它理解为损失函数，C为权重，用以表示该样本不满足约束的程度，C值越大，对分错样本的惩罚力度越大，在训练样本中准确度高，但泛化能力弱；如果减小C的话，则容许训练样本中有一些错误分类，容许有噪声情况，但泛化能力强。

支持向量机特点：

- 在小规模数据训练中，SVM相比较LR、随机森林等分类器，效果更好；

- 在非线性特征空间中，效果较好；

- 在数据量庞大的情况下，效果不一定好；

- SVM不能产生分类的概率值，

支持向量机被认为是在文本分类领域效果最好的机器学习算法，在工业界主要应用在网页分类、微博情感分析、舆情监控、用户评论挖掘、文本过滤等诸多领域。

-- SVM在Sklearn中的应用

-Python 代码

import pandas as pd
from sklearn import datasets
from sklearn.cross_validation import train_test_split
from sklearn.metrics import accuracy_score
from sklearn import svm
breast_data = datasets.load_breast_cancer()
data = pd.DataFrame(datasets.load_breast_cancer().data)
data.columns = breast_data['feature_names']
data_np = breast_data['data']
target_np = breast_data['target']
train_X,test_X, train_y, test_y = train_test_split(data_np,target_np,test_size = 0.1,random_state = 0)
'''
  采用线性核函数进行分类
  kernel可用参数：
  "linear": 线性核函数
  "poly":   多项式核函数
  "rbf" :   径像核函数/高斯核函数
  "sigmoid":核矩阵
'''
model = svm.SVC(kernel='linear', C=2.0)
model.fit(train_X, train_y)
y_pred = model.predict(test_X)
print(accuracy_score(test_y, y_pred))

作者：华为云专家周捷

往期文章精选

如果让你手写个栈和队列，你还会写吗？

挑战10个最难的Java面试题（附答案）【上】

javascript基础修炼(13)——记一道有趣的JS脑洞练习题

【我的物联网成长记3】如何开发物联网应用？

【HC资料合集】2019华为全联接大会主题资料一站式汇总，免费下载！

对你没有看错！不到 10 行代码完成抖音热门视频的爬取！

Python面试的一些心得，与Python练习题分享