十一次作业——LL(1)文法的判断，递归下降分析程序

1. 文法 G（S）:

（1）S -> AB

（2）A ->Da|ε

（3）B -> cC

（4）C -> aADC |ε

（5）D -> b|ε

验证文法 G（S）是不是 LL（1）文法？

解：

FIRST集：

FIRST（Da）={b,a}

FIRST（ε）={ε}

FIRST（aADC）={a}

FIRST（b）={b}

FOLLOW集：

FOLLOW(A)=FIRST(B)+FIRST(B)+FIRST(B)+FOLLOW(C)={c,a,b,#}

FOLLOW(C)={#}

FOLLOW(D)={a,#}

SELECT集：

SELECT(A->Da)={b,a}

SELECT(A->ε)={c,b,a,#}

SELECT(C->aADC)={a}

SELECT(C->ε)={#}

SELECT(D->b)={b}

SELECT(D->ε)={a,#}

因为：

SELECT(A->Da)∩SELECT(A->ε)≠∅

所以此文法不为LL(1)文法。

2.法消除左递归之后的表达式文法是否是LL(1)文法？

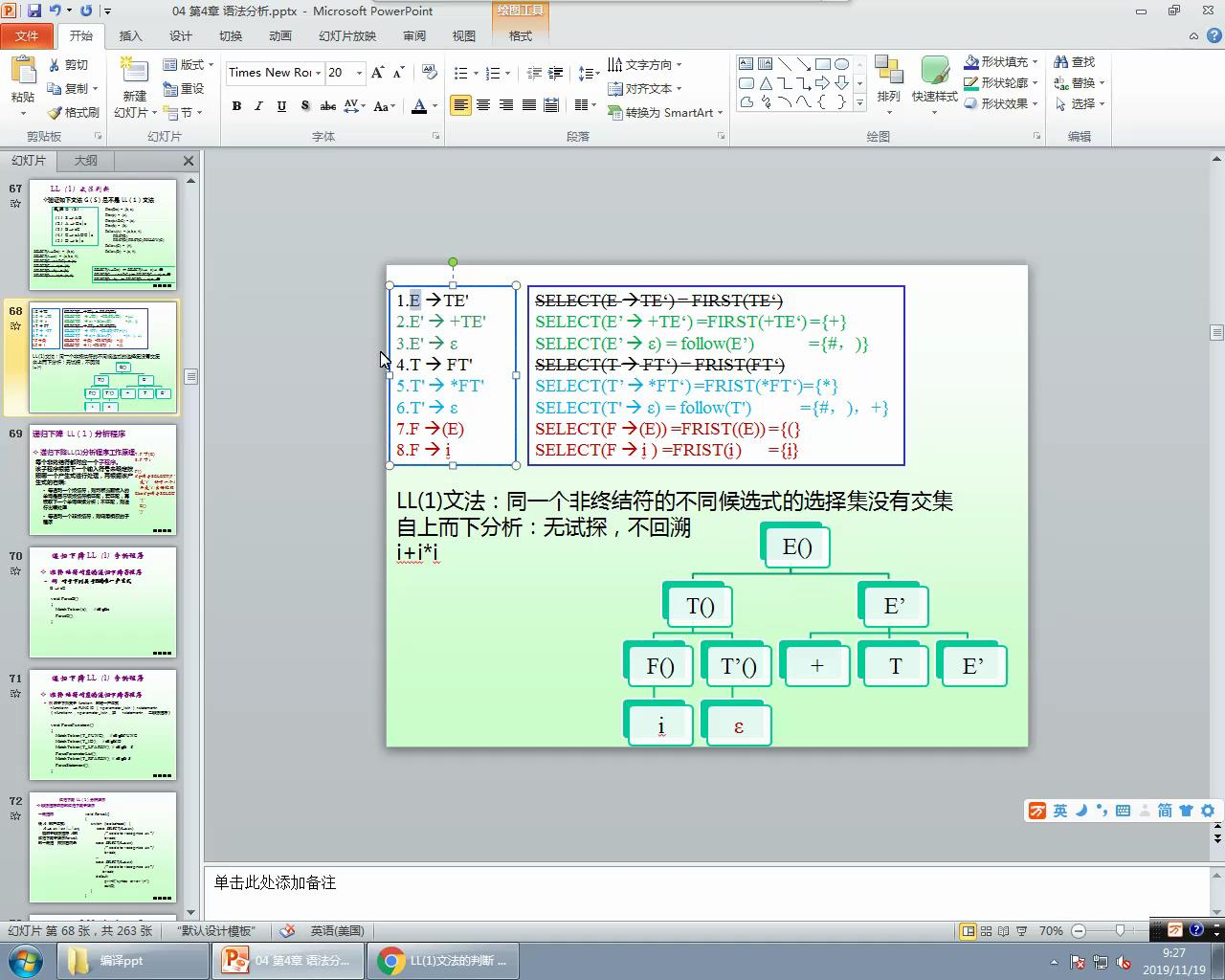
答：是LL（1）文法。

3.接2，如果是LL(1)文法，写出它的递归下降语法分析程序代码。

E()

｛T();

E'();

}

E'()

T()

T'()

F()

答：

void ParseE()｛

　　ParseT();

ParseE'();

}

void ParseT()  {　　

　　ParseF();

　　ParseT'();

}

void ParseE'()  {

　　switch(lookahead):

　　　　case +:

　　　　　　MatchToken(+);

　　　　　　ParseT();

　　　　　　ParseE'();

　　　　　　break;

　　　　case #:

　　　　　　break;

　　　　case ):

　　　　　　break;

　　　　default:

　　　　　　printf('synax error!\n');

　　　　　　exit(0);

}

void ParseF()  {　

　　switch(lookahead):

　　　　case (:

　　　　　　MatchToken(()；

　　　　　　ParseE()；
　　　　　　MatchToken())；

　　　　　　break;

　　　　case i:

　　　　　　MatchToken(i);

　　　　　　break;

　　　　default:

　　　　　　printf('synax error!\n');

　　　　　　exit(0);

}

void ParseT'()

{

　　switch(lookahead):

　　　　case *:

　　　　　　ParseF();

　　　　　　MatchToken(*);

　　　　　　ParseT'();

　　　　　　break;

　　　　case #:

　　　　　　break;

　　　　case ):

　　　　　　break;

　　　　case +:

　　　　　　break;

　　　　default:

　　　　　　printf('synax error!\n');

　　　　　　exit(0);

}

4.加上实验一的词法分析程序，形成可运行的语法分析程序，分析任意输入的符号串是不是合法的表达式。