JavaScript 数据结构与算法之美 - 桶排序、计数排序、基数排序

1. 前言

算法为王。

想学好前端，先练好内功，只有内功深厚者，前端之路才会走得更远。

笔者写的 JavaScript 数据结构与算法之美 系列用的语言是 JavaScript ，旨在入门数据结构与算法和方便以后复习。

之所以把 计数排序、桶排序、基数排序 放在一起比较，是因为它们的平均时间复杂度都为 O(n)。

因为这三个排序算法的时间复杂度是线性的，所以我们把这类排序算法叫作 线性排序（Linear sort）。

之所以能做到线性的时间复杂度，主要原因是，这三个算法不是基于比较的排序算法，都不涉及元素之间的比较操作。

另外，请大家带着问题来阅读下文，问题：如何根据年龄给 100 万用户排序？

2. 桶排序（Bucket Sort）

桶排序是计数排序的升级版，也采用了分治思想。

思想

将要排序的数据分到有限数量的几个有序的桶里。
每个桶里的数据再单独进行排序（一般用插入排序或者快速排序）。
桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。

比如：

桶排序利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。

为了使桶排序更加高效，我们需要做到这两点：

在额外空间充足的情况下，尽量增大桶的数量。
使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中。

桶排序的核心：就在于怎么把元素平均分配到每个桶里，合理的分配将大大提高排序的效率。

实现

// 桶排序

const bucketSort = (array, bucketSize) => {

  if (array.length === 0) {

    return array;

  }

  console.time('桶排序耗时');

  let i = 0;

  let minValue = array[0];

  let maxValue = array[0];

  for (i = 1; i < array.length; i++) {

    if (array[i] < minValue) {

      minValue = array[i]; //输入数据的最小值

    } else if (array[i] > maxValue) {

      maxValue = array[i]; //输入数据的最大值

    }

  }

  //桶的初始化

  const DEFAULT_BUCKET_SIZE = 5; //设置桶的默认数量为 5

  bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;

  const bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;

  const buckets = new Array(bucketCount);

  for (i = 0; i < buckets.length; i++) {

    buckets[i] = [];

  }

  //利用映射函数将数据分配到各个桶中

  for (i = 0; i < array.length; i++) {

    buckets[Math.floor((array[i] - minValue) / bucketSize)].push(array[i]);

  }

  array.length = 0;

  for (i = 0; i < buckets.length; i++) {

    quickSort(buckets[i]); //对每个桶进行排序，这里使用了快速排序

    for (var j = 0; j < buckets[i].length; j++) {

      array.push(buckets[i][j]);

    }

  }

  console.timeEnd('桶排序耗时');

  return array;

};

// 快速排序

const quickSort = (arr, left, right) => {

	let len = arr.length,

		partitionIndex;

	left = typeof left != 'number' ? 0 : left;

	right = typeof right != 'number' ? len - 1 : right;

	if (left < right) {

		partitionIndex = partition(arr, left, right);

		quickSort(arr, left, partitionIndex - 1);

		quickSort(arr, partitionIndex + 1, right);

	}

	return arr;

};

const partition = (arr, left, right) => {

	//分区操作

	let pivot = left, //设定基准值（pivot）

		index = pivot + 1;

	for (let i = index; i <= right; i++) {

		if (arr[i] < arr[pivot]) {

			swap(arr, i, index);

			index++;

		}

	}

	swap(arr, pivot, index - 1);

	return index - 1;

};

const swap = (arr, i, j) => {

	let temp = arr[i];

	arr[i] = arr[j];

	arr[j] = temp;

};

测试

const array = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2];

console.log('原始array:', array);

const newArr = bucketSort(array);

console.log('newArr:', newArr);

// 原始 array:  [4, 6, 8, 5, 9, 1, 2, 5, 3, 2]

// 堆排序耗时:   0.133056640625ms

// newArr:  	 [1, 2, 2, 3, 4, 5, 5, 6, 8, 9]

分析

第一，桶排序是原地排序算法吗？

因为桶排序的空间复杂度，也即内存消耗为 O(n)，所以不是原地排序算法。

第二，桶排序是稳定的排序算法吗？

取决于每个桶的排序方式，比如：快排就不稳定，归并就稳定。

第三，桶排序的时间复杂度是多少？

因为桶内部的排序可以有多种方法，是会对桶排序的时间复杂度产生很重大的影响。所以，桶排序的时间复杂度可以是多种情况的。

总的来说

最佳情况：当输入的数据可以均匀的分配到每一个桶中。

最差情况：当输入的数据被分配到了同一个桶中。

以下是桶的内部排序为快速排序的情况：

如果要排序的数据有 n 个，我们把它们均匀地划分到 m 个桶内，每个桶里就有 k =n / m 个元素。每个桶内部使用快速排序，时间复杂度为 O(k * logk)。

m 个桶排序的时间复杂度就是 O(m * k * logk)，因为 k = n / m，所以整个桶排序的时间复杂度就是 O(n*log(n/m))。

当桶的个数 m 接近数据个数 n 时，log(n/m) 就是一个非常小的常量，这个时候桶排序的时间复杂度接近 O(n)。

最佳情况：T(n) = O(n)。当输入的数据可以均匀的分配到每一个桶中。

最差情况：T(n) = O(nlogn)。当输入的数据被分配到了同一个桶中。

平均情况：T(n) = O(n)。

桶排序最好情况下使用线性时间 O(n)，桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为 O(n)。

很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少。但相应的空间消耗就会增大。

适用场景

桶排序比较适合用在外部排序中。
外部排序就是数据存储在外部磁盘且数据量大，但内存有限，无法将整个数据全部加载到内存中。

动画

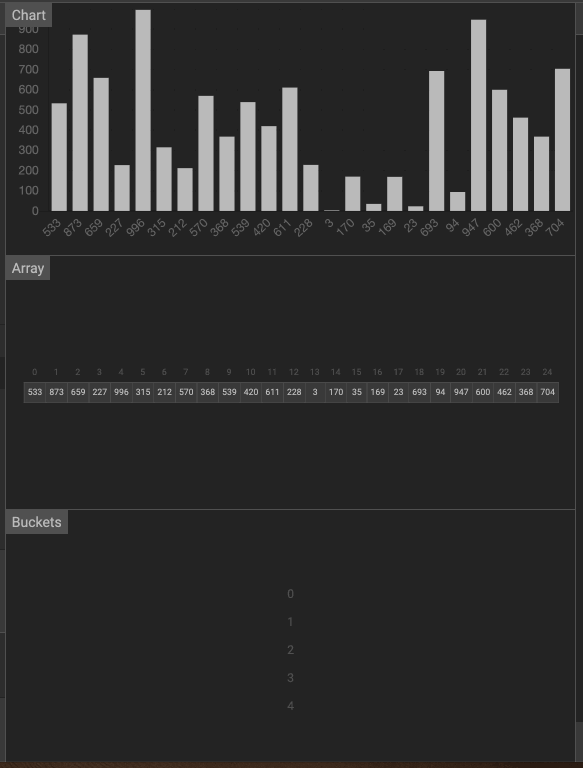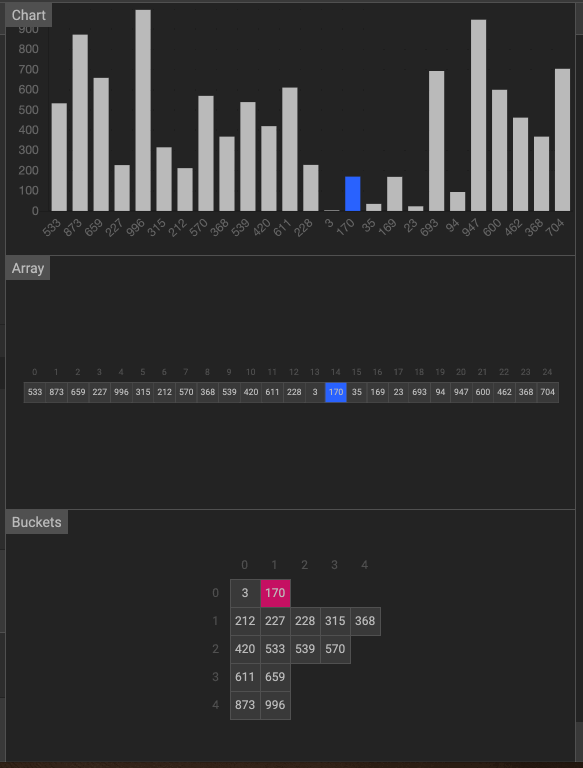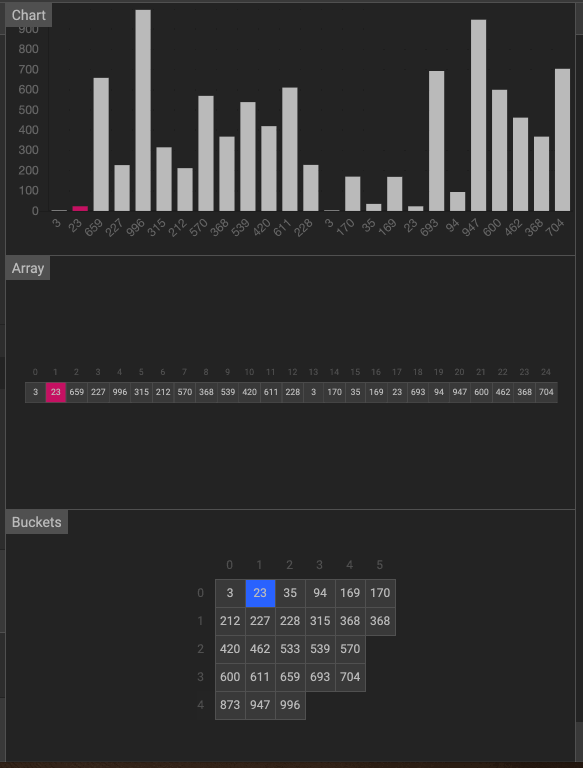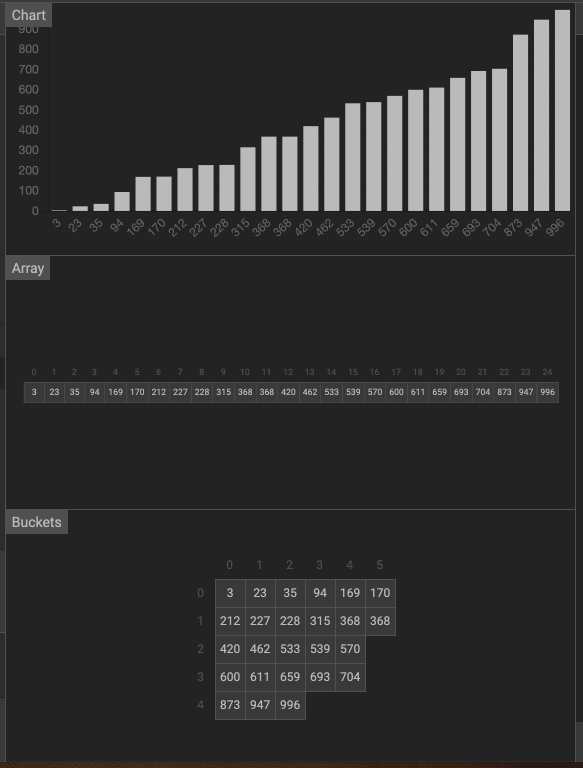
3. 计数排序（Counting Sort）

思想

找出待排序的数组中最大和最小的元素。
统计数组中每个值为 i 的元素出现的次数，存入新数组 countArr 的第 i 项。
对所有的计数累加（从 countArr 中的第一个元素开始，每一项和前一项相加）。
反向填充目标数组：将每个元素 i 放在新数组的第 countArr[i] 项，每放一个元素就将 countArr[i] 减去 1 。

关键在于理解最后反向填充时的操作。

使用条件

只能用在数据范围不大的场景中，若数据范围 k 比要排序的数据 n 大很多，就不适合用计数排序。
计数排序只能给非负整数排序，其他类型需要在不改变相对大小情况下，转换为非负整数。
比如如果考试成绩精确到小数后一位，就需要将所有分数乘以 10，转换为整数。

实现

方法一：

const countingSort = array => {

	let len = array.length,

		result = [],

		countArr = [],

		min = (max = array[0]);

	console.time('计数排序耗时');

	for (let i = 0; i < len; i++) {

		// 获取最小，最大 值

		min = min <= array[i] ? min : array[i];

		max = max >= array[i] ? max : array[i];

		countArr[array[i]] = countArr[array[i]] ? countArr[array[i]] + 1 : 1;

	}

	console.log('countArr :', countArr);

	// 从最小值 -> 最大值,将计数逐项相加

	for (let j = min; j < max; j++) {

		countArr[j + 1] = (countArr[j + 1] || 0) + (countArr[j] || 0);

	}

	console.log('countArr 2:', countArr);

	// countArr 中,下标为 array 数值，数据为 array 数值出现次数；反向填充数据进入 result 数据

	for (let k = len - 1; k >= 0; k--) {

		// result[位置] = array 数据

		result[countArr[array[k]] - 1] = array[k];

		// 减少 countArr 数组中保存的计数

		countArr[array[k]]--;

		// console.log("array[k]:", array[k], 'countArr[array[k]] :', countArr[array[k]],)

		console.log('result:', result);

	}

	console.timeEnd('计数排序耗时');

	return result;

};

测试

const array = [2, 2, 3, 8, 7, 1, 2, 2, 2, 7, 3, 9, 8, 2, 1, 4, 2, 4, 6, 9, 2];

console.log('原始 array: ', array);

const newArr = countingSort(array);

console.log('newArr: ', newArr);

// 原始 array:  [2, 2, 3, 8, 7, 1, 2, 2, 2, 7, 3, 9, 8, 2, 1, 4, 2, 4, 6, 9, 2]

// 计数排序耗时:   5.6708984375ms

// newArr:  	 [1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 4, 4, 6, 7, 7, 8, 8, 9, 9]

方法二：

const countingSort2 = (arr, maxValue) => {

	console.time('计数排序耗时');

	maxValue = maxValue || arr.length;

	let bucket = new Array(maxValue + 1),

		sortedIndex = 0;

	(arrLen = arr.length), (bucketLen = maxValue + 1);

	for (let i = 0; i < arrLen; i++) {

		if (!bucket[arr[i]]) {

			bucket[arr[i]] = 0;

		}

		bucket[arr[i]]++;

	}

	for (let j = 0; j < bucketLen; j++) {

		while (bucket[j] > 0) {

			arr[sortedIndex++] = j;

			bucket[j]--;

		}

	}

	console.timeEnd('计数排序耗时');

	return arr;

};

测试

const array2 = [2, 2, 3, 8, 7, 1, 2, 2, 2, 7, 3, 9, 8, 2, 1, 4, 2, 4, 6, 9, 2];

console.log('原始 array2: ', array2);

const newArr2 = countingSort2(array2, 21);

console.log('newArr2: ', newArr2);

// 原始 array:  [2, 2, 3, 8, 7, 1, 2, 2, 2, 7, 3, 9, 8, 2, 1, 4, 2, 4, 6, 9, 2]

// 计数排序耗时:   0.043212890625ms

// newArr:  	 [1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 4, 4, 6, 7, 7, 8, 8, 9, 9]

例子

可以认为，计数排序其实是桶排序的一种特殊情况。

当要排序的 n 个数据，所处的范围并不大的时候，比如最大值是 k，我们就可以把数据划分成 k 个桶。每个桶内的数据值都是相同的，省掉了桶内排序的时间。

我们都经历过高考，高考查分数系统你还记得吗？我们查分数的时候，系统会显示我们的成绩以及所在省的排名。如果你所在的省有 50 万考生，如何通过成绩快速排序得出名次呢？

考生的满分是 900 分，最小是 0 分，这个数据的范围很小，所以我们可以分成 901 个桶，对应分数从 0 分到 900 分。
根据考生的成绩，我们将这 50 万考生划分到这 901 个桶里。桶内的数据都是分数相同的考生，所以并不需要再进行排序。
我们只需要依次扫描每个桶，将桶内的考生依次输出到一个数组中，就实现了 50 万考生的排序。
因为只涉及扫描遍历操作，所以时间复杂度是 O(n)。

分析

第一，计数排序是原地排序算法吗？

因为计数排序的空间复杂度为 O(k)，k 是桶的个数，所以不是原地排序算法。
第二，计数排序是稳定的排序算法吗？

计数排序不改变相同元素之间原本相对的顺序，因此它是稳定的排序算法。
第三，计数排序的时间复杂度是多少？

最佳情况：T(n) = O(n + k)

最差情况：T(n) = O(n + k)

平均情况：T(n) = O(k)

k：桶的个数。

动画

4. 基数排序（Radix Sort）

思想

基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。

由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

例子

假设我们有 10 万个手机号码，希望将这 10 万个手机号码从小到大排序，你有什么比较快速的排序方法呢？

这个问题里有这样的规律：假设要比较两个手机号码 a，b 的大小，如果在前面几位中，a 手机号码已经比 b 手机号码大了，那后面的几位就不用看了。所以是基于位来比较的。

桶排序、计数排序能派上用场吗？手机号码有 11 位，范围太大，显然不适合用这两种排序算法。针对这个排序问题，有没有时间复杂度是 O(n) 的算法呢？有，就是基数排序。

使用条件

要求数据可以分割独立的位来比较；
位之间由递进关系，如果 a 数据的高位比 b 数据大，那么剩下的地位就不用比较了；
每一位的数据范围不能太大，要可以用线性排序，否则基数排序的时间复杂度无法做到 O(n)。

方案

按照优先从高位或低位来排序有两种实现方案:

MSD：由高位为基底，先按 k1 排序分组，同一组中记录, 关键码 k1 相等，再对各组按 k2 排序分成子组, 之后，对后面的关键码继续这样的排序分组，直到按最次位关键码 kd 对各子组排序后，再将各组连接起来，便得到一个有序序列。MSD 方式适用于位数多的序列。
LSD：由低位为基底，先从 kd 开始排序，再对 kd - 1 进行排序，依次重复，直到对 k1 排序后便得到一个有序序列。LSD 方式适用于位数少的序列。

实现

/**

	* name: 基数排序

	* @param  array 待排序数组

	* @param  max 最大位数

	*/

const radixSort = (array, max) => {

	console.time('计数排序耗时');

	const buckets = [];

	let unit = 10,

		base = 1;

	for (let i = 0; i < max; i++, base *= 10, unit *= 10) {

		for (let j = 0; j < array.length; j++) {

			let index = ~~((array[j] % unit) / base); //依次过滤出个位，十位等等数字

			if (buckets[index] == null) {

				buckets[index] = []; //初始化桶

			}

			buckets[index].push(array[j]); //往不同桶里添加数据

		}

		let pos = 0,

			value;

		for (let j = 0, length = buckets.length; j < length; j++) {

			if (buckets[j] != null) {

				while ((value = buckets[j].shift()) != null) {

					array[pos++] = value; //将不同桶里数据挨个捞出来，为下一轮高位排序做准备，由于靠近桶底的元素排名靠前，因此从桶底先捞

				}

			}

		}

	}

	console.timeEnd('计数排序耗时');

	return array;

};

测试

const array = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];

console.log('原始array:', array);

const newArr = radixSort(array, 2);

console.log('newArr:', newArr);

// 原始 array:  [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]

// 堆排序耗时:   0.064208984375ms

// newArr:  	 [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

分析

第一，基数排序是原地排序算法吗？

因为计数排序的空间复杂度为 O(n + k)，所以不是原地排序算法。
第二，基数排序是稳定的排序算法吗？

基数排序不改变相同元素之间的相对顺序，因此它是稳定的排序算法。
第三，基数排序的时间复杂度是多少？

最佳情况：T(n) = O(n * k)

最差情况：T(n) = O(n * k)

平均情况：T(n) = O(n * k)

k 是待排序列最大值。

动画

LSD 基数排序动图演示：

5. 解答开篇

回过头来看看开篇的思考题：如何根据年龄给 100 万用户排序？

你可能会说，我用上一节讲的归并、快排就可以搞定啊！是的，它们也可以完成功能，但是时间复杂度最低也是 O(nlogn)。

有没有更快的排序方法呢？以下是参考答案。

实际上，根据年龄给 100 万用户排序，就类似按照成绩给 50 万考生排序。
我们假设年龄的范围最小 1 岁，最大不超过 120 岁。
我们可以遍历这 100 万用户，根据年龄将其划分到这 120 个桶里，然后依次顺序遍历这 120 个桶中的元素。
这样就得到了按照年龄排序的 100 万用户数据。

6. 复杂性对比

基数排序 vs 计数排序 vs 桶排序

基数排序有两种方法：

MSD 从高位开始进行排序
LSD 从低位开始进行排序

这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：

基数排序：根据键值的每位数字来分配桶；
计数排序：每个桶只存储单一键值；
桶排序：每个桶存储一定范围的数值；

复杂性对比

名称	平均	最好	最坏	空间	稳定性	排序方式
桶排序	O(n + k)	O(n + k)	O(n²)	O(n + k)	Yes	Out-place
计数排序	O(n + k)	O(n + k)	O(n + k)	O(k)	Yes	Out-place
基数排序	O(n * k)	O(n * k)	O(n * k)	O(n + k)	Yes	Out-place

n: 数据规模

桶排序的时间复杂度可以是多种情况的，取决于桶内的排序。

7. 最后

文中所有的代码及测试事例都已经放到我的 GitHub 上了。

觉得有用？喜欢就收藏，顺便点个赞吧，你的支持是我最大的鼓励！

参考文章：