cs231n---强化学习

介绍了基于价值函数和基于策略梯度的两种强化学习框架，并介绍了四种强化学习算法：Q-learning，DQN，REINFORCE，Actot-Critic

1 强化学习问题建模

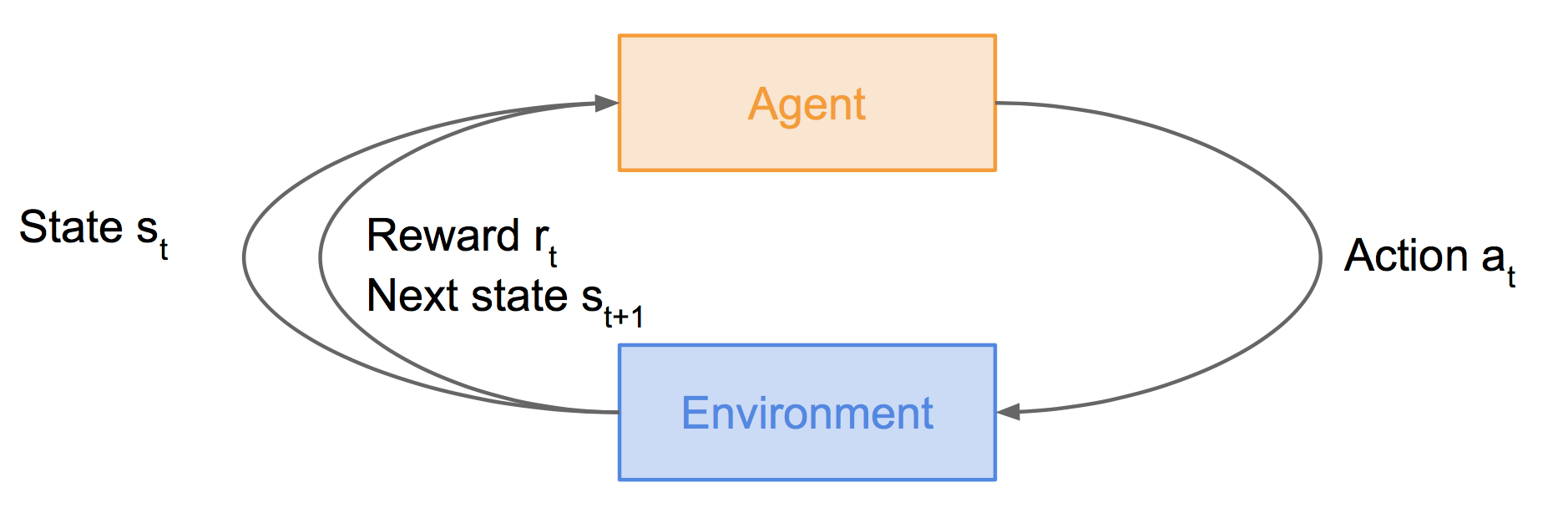
上图中，智能体agent处于状态st下，执行动作at后，会由于周围环境的作用进入下一个状态st+1，同时获得奖励rt。

马尔可夫决策过程MDP建模了上图过程：

我们定义策略Pi为一个从状态s到动作a的函数，表示在状态s下采取什么样的动作a。

而我们的目标是，找到一个最好的策略pi，使得整个过程中累计的奖励值最大：

比较正式的表达是：

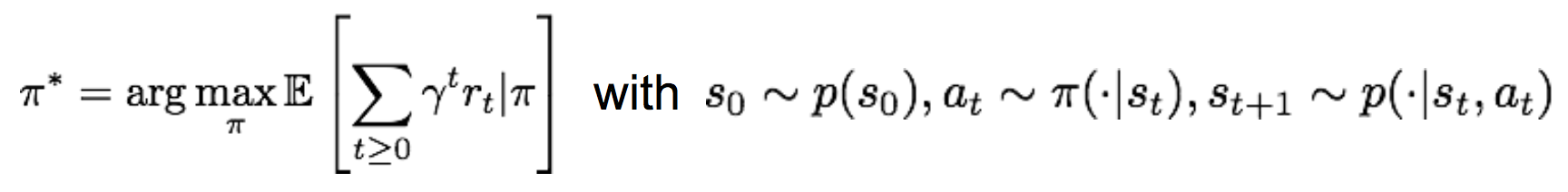
2 Q-learning算法

（1）价值函数与Q-价值函数

对于一个给定的策略pi，只要我们给定初始状态s0，就能产生序列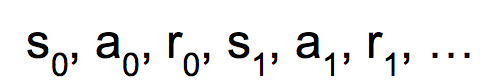

那么，只要给定一个策略pi，就能计算出在状态s下所产生的累积奖励的期望，也就是价值函数：

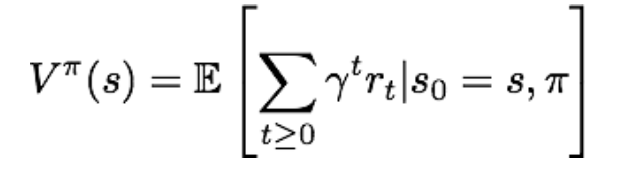
注意，价值函数评价了给定策略pi下状态s的价值，由策略pi和当前状态s所唯一确定。

类似的，Q-价值函数则评价了给定策略pi下，在状态s下采取动作a后，所能带来的累积奖励期望：

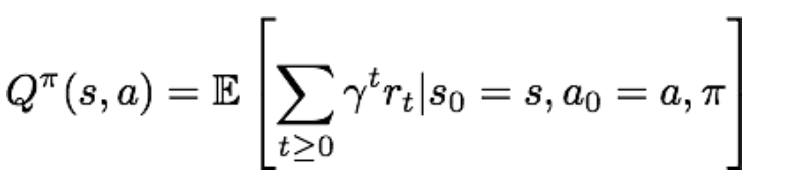
Q-价值函数由策略pi和当前状态s和当前动作a所唯一确定。

（2）贝尔曼方程

现在我们固定当前状态s和当前动作a，那么目标就是要选择最优策略pi，使得Q-value函数最大，这个最优的Q-value函数被记为Q*：

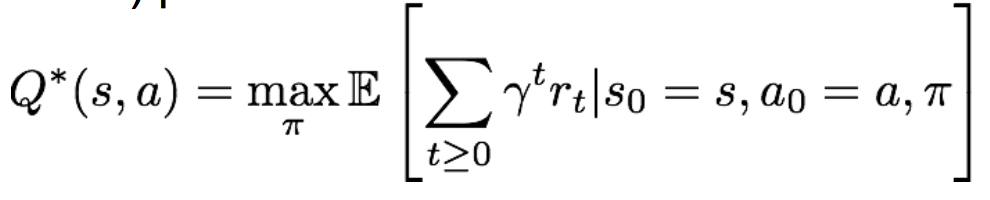
理解一下Q*，也就是在当前状态s下采取动作a后，所能达到的最大累积奖励期望。显然Q*仅与s和a有关。

而强化学习方法Q-learning的核心公式——贝尔曼方程，则给出了Q*的另一种表达形式：

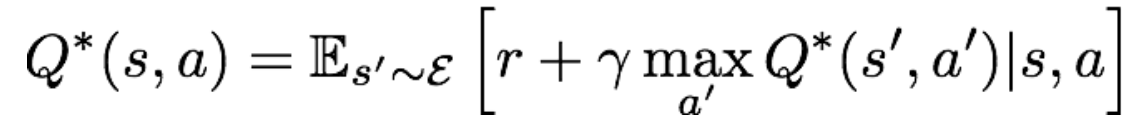
对公式的理解为：当我们在状态s下采取动作a后，环境会反馈给我们一个奖励r，以及下一时刻的状态s'。记下一时刻的动作为a'，这样我们就能递归地使用Q*函数。

（3）Q-learning

现在让我们来看一种经典的强化学习算法，Q-learning。

Q-learning中，我们需要一张称为Q-table的查找表，该表第i行第j列的元素表示Q*(si, aj)的值。

然而我们并不知道Q*的具体形式以及值，我们只能一开始使用全0初始化Q-table，然后进行游戏，每执行一个动作后，使用贝尔曼方程去更新Q-table的值，理论研究表明当迭代次数足够多后，Q-table的值将会收敛为真实的Q*值。这也被称为值迭代算法：

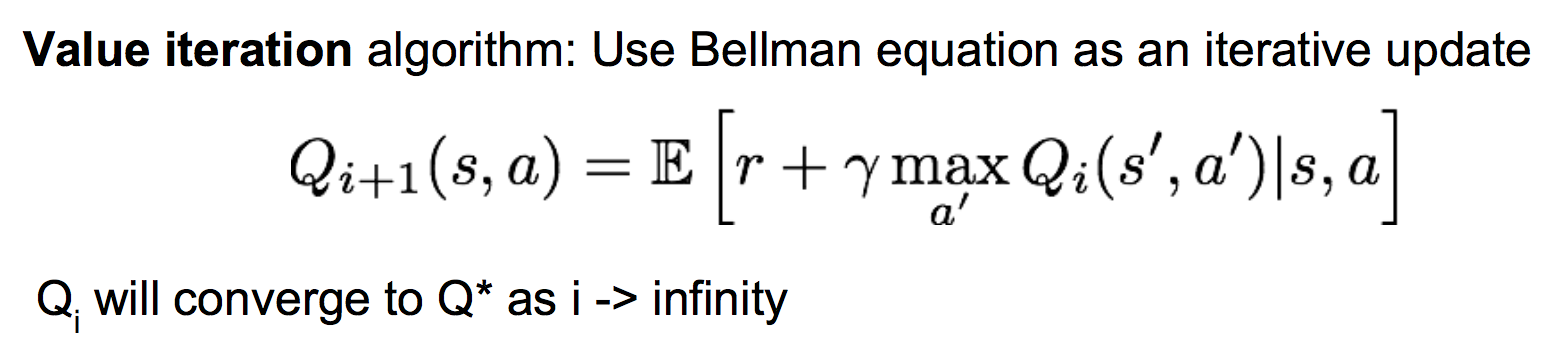
Qi和Qi+1分别表示更新前和更新后的Q-table。

Q-learning的完整算法过程为：

3  深度强化学习----Deep Q-learning

传统的Q-learning算法当遇到状态空间很大时（例如状态是一个游戏画面的所有像素），我们不可能用表Q-table来枚举出所有的状态及其对应的动作a的所有q值。而Q*这个函数是我们最终要学习的，并且它很复杂。很自然地，我们想到用一个神经网络来表示Q*，并且在游戏中去不断的学习它！

前向传播和反向传播表示为：

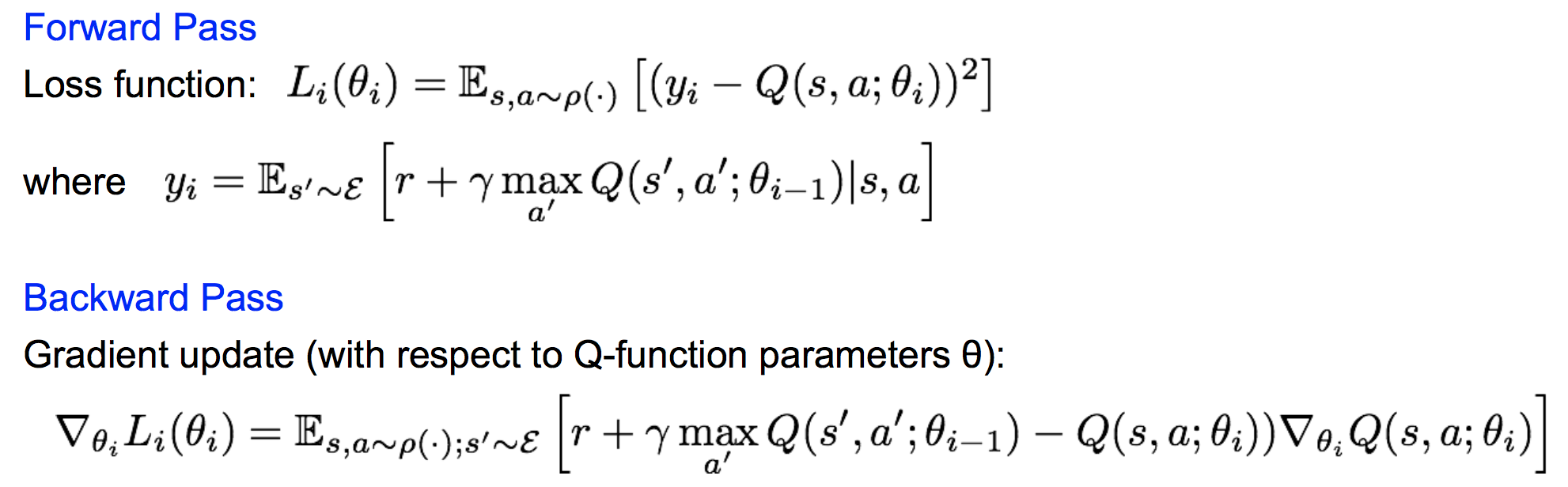
直接这样还不能有效的学习。原因有两点：

因此我们使用一个叫做Experience Replay的机制，每次将生成的(st, at, rt, st+1)元组放入一个表中，然后每次训练Q网络时，从该表中随机取一批mini batch进行训练。

完整的Deep Q-learning算法为：

注意这里我们每次有一定概率去随机的行动，这样做的目的是探索更大的状态空间。

4 策略梯度

（1）引入策略梯度

为什么要用策略梯度：基于价值函数的方法，当状态空间很大时，价值函数会很复杂以至于难以学习。而策略函数（已知当前状态下各个动作的条件概率分布）则会比较简单。因此我们这里会去学习一个策略网络，而不是价值网络。

策略网络的定义如下：

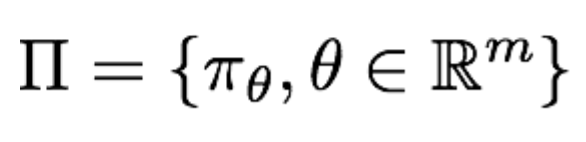
表示策略网络的参数为θ，所有参数的可能取值构成了所有可能的策略。

对一个给定的策略，其价值定义为：

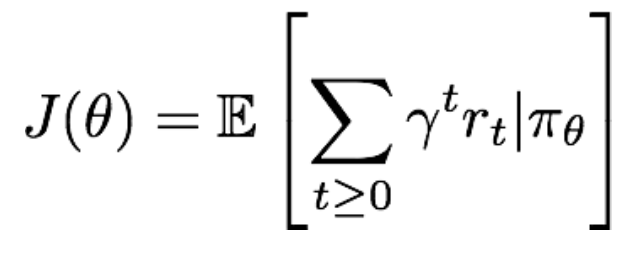
那么，我们要找到最优的参数θ，使得上面的J(θ)最大。即：。显然要使用gradient ascent的方法，那么如何来计算策略参数的梯度呢？

（2）REINFORCE 计算策略梯度

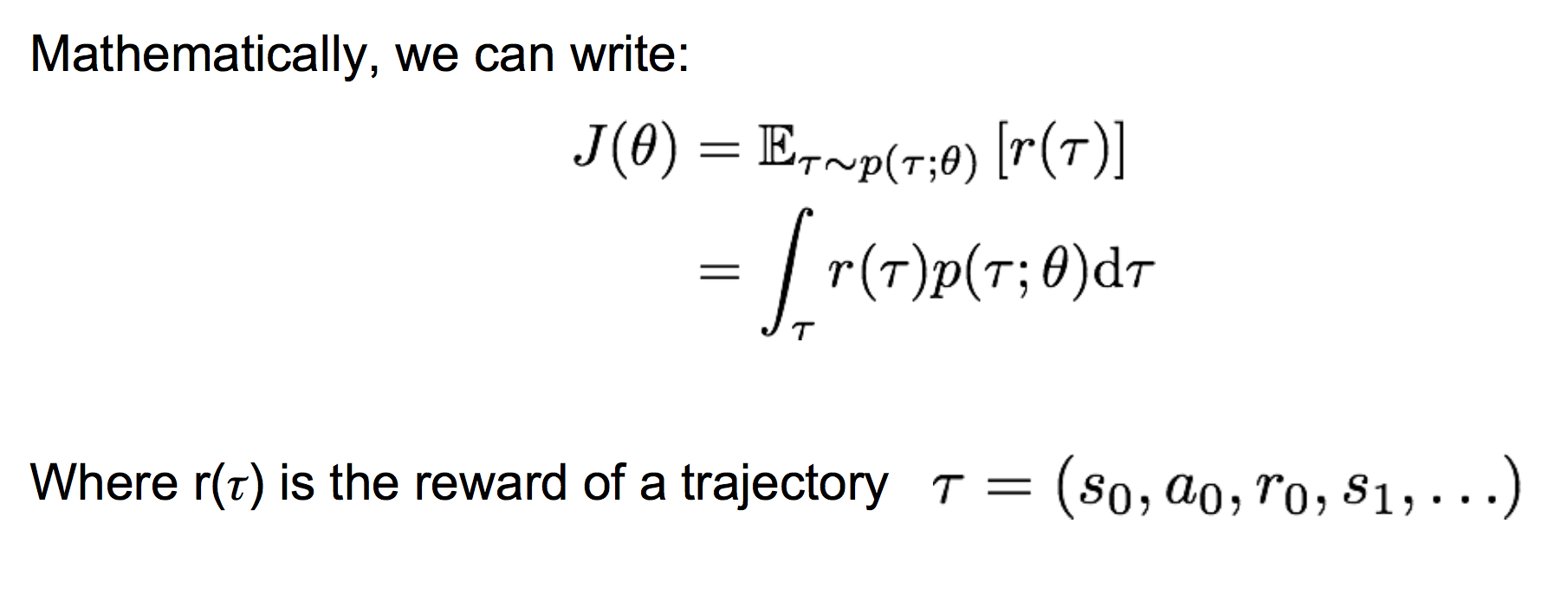
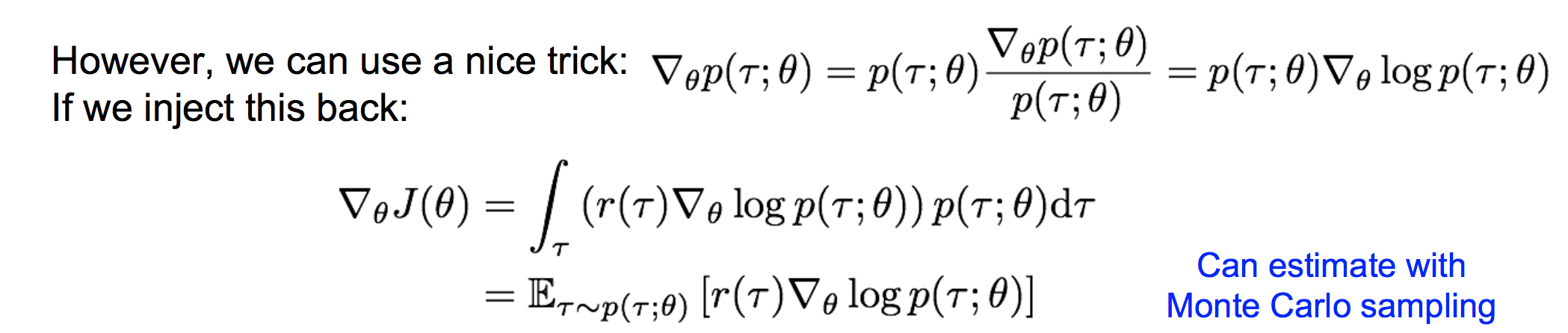
这样，我们就可以采样出若干个轨迹τ，来估计策略梯度。注意这里的估计是一个无偏估计。

（3）直观上理解策略梯度的表达式

注意看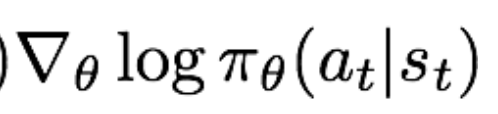，这一项表示当前的梯度方向是使得各个时间步的动作出现似然增大的梯度方向，前面再加一个权重r(τ)。则当r(τ)高时，对应于该轨迹的各个动作似然要相对增大，当r(τ)低时，对应于该轨迹的各个动作似然要相对减小。很符合我们的直观感受。