基于记忆性的中值滤波O(r)与O(1)复杂度的算法实现

　　本文参考博客：https://www.cnblogs.com/Imageshop/archive/2013/04/26/3045672.html

　　原生的中值滤波是基于排序算法的，这样的算法复杂度基本在O(r²)左右，当滤波半径较大时，排序算法就显得很慢。对此有多种改进算法，这里介绍经典

的Huang算法与O(1)算法，两者都是基于记忆性的算法，只是后者记性更强。

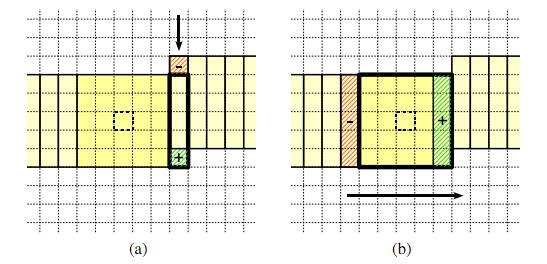
　　排序算法明显的一个不足之处就是无记忆性。当核向右移动一列后，只是核的最左和最右列数据发生了变化，中间不变的数据应当被存储起来，而排序算法

并没有做到这点。Huang算法的思想是建立一个核直方图，来统计核内的各灰度的像素数。当核向右移动时，就将新的一列所有数据加入到直方图中，同时将最

左列的旧数据从直方图中删除，如下图所示。这样做使得大部分数据能够被记忆，减少重复操作。当直方图更新完毕后，就可以通过从左到右累计像素来找到中值。

　　　　　　　　　　　　　　

下面是算法具体实现步骤与代码：

　　1.每行开始都将直方图、像素计数、中值变量清零，将核覆盖的所有像素加到直方图中。

　　2.计算中值，sumcnt为小于中值灰度的像素数和。如果当前sumcnt大于等于阈值，则表明，实际中值比当前median小，则直方图向左减去像素数，同时median

　　　也减小，直到sumcnt小于阈值，则此时median为中值（sumcnt加上中值像素数将大于或等于阈值）；如果sumcnt加上median像素数仍小于阈值，表明，实

　　　际中值比当前median大，则直方图向右累加像素数，同时median增加，直到sumcnt加上median像素数大于等于阈值，则此时median为中值（sumcnt小于阈值）。

　　3.核每向右移动一列，更新核直方图，比较每一个新加入的灰度值与median，小于则median加1，比较每一个减去的灰度值与median，小于则median减1。执行

　　　一次步骤2后继续移动核，直到整幅图都被滤波完毕。

%中值滤波黄法
%输入：8位深度图像、滤波半径（*3的半径为1,中值百分比）
function grayimg=medianfilterhuang(grayimg,radius,percentage)
    [sizex,sizey]=size(grayimg);
    thres=int16(((*radius+)^*percentage));
    %扩展边界
    extendimg=int16(horzcat(repmat(grayimg(:,),,radius),grayimg,repmat(grayimg(:,sizey),,radius)));
    extendimg=int16(vertcat(repmat(extendimg(,:),radius,),extendimg,repmat(extendimg(sizex,:),radius,)));
    for i=radius+:sizex+radius
        %初始化直方图，每行第一个将所有像素加入直方图
        histogram=int16(zeros(,));
        sumcnt=int16();
        median=int16();
        for j=radius+:sizey+radius
            %遍历卷积覆盖行
            for k=i-radius:i+radius
                if (j>radius+)
                    %删去左列，加入新右列
                    histogram(extendimg(k,j-radius-)+)=histogram(extendimg(k,j-radius-)+)-;
                    histogram(extendimg(k,j+radius)+)=histogram(extendimg(k,j+radius)+)+;
                    %只关心中值灰度以左的像素数量
                    if (extendimg(k,j-radius-)<median)
                        sumcnt=sumcnt-;
                    end
                    if (extendimg(k,j+radius)<median)
                        sumcnt=sumcnt+;
                    end
                else
                    %行首
                    for h=j-radius:j+radius
                        histogram(extendimg(k,h)+)=histogram(extendimg(k,h)+)+;
                    end
                end
            end
            %sumcnt不将中值像素数累加进去
            %旧中值偏大
            while(sumcnt>=thres)
                median=median-;
                sumcnt=sumcnt-histogram(median+);
            end
            %旧中值偏小
            while(sumcnt+histogram(median+)<thres)
                sumcnt=sumcnt+histogram(median+);
                median=median+;
            end
            grayimg(i-radius,j-radius)=median;
        end
    end
end

Huang算法

　　性能分析发现，Huang算法的大部分时间花在了更新核直方图上。并且由于它是O(r)的复杂度，因此当滤波半径变大后，更新直方图部分花费的时间也变多，而计算

中值部分所花时间一直都是固定的，因为它的复杂度是O(1)，与滤波半径无关。那么为了使直方图更新的复杂度能降到O(1)，就要增强算法的记忆性。可以看到以相邻行

相同列为中心的核之间也存在重合，这跟之前以相邻列相同行为中心的核存在重合类似。于是，我们可以为每列都维护一个直方图，而核直方图可以由这些列直方图相加

得到，更新核的时候，最右边的一列直方图向下移动一行，就更新了列直方图，再减去最左边一列直方图，核就得到更新。这样每次更新直方图都只要移动一次列直方图，

而其余的都是直方图的加减操作，值得注意的是，这样的实现很完美得利用了可并行的矩阵加减来代替顺序执行的for迭代。因此，虽然更新过程看上去有许多加减操作，

实际上都是可快速并行执行的。

　　　　　　　　

　　还有一点，由于并行化的矩阵加减，就不能用sumcnt来跟踪阈值变化了。如果直接迭代累加直方图，最坏的情况是要执行255加法。为了使中值计算更快，可以采用

两层直方图，高层用于保存高4位（直方图大小为16*1），低层保存全位（直方图大小为256*1）。每次先累加高层进行范围缩小，再从相应范围累加低层找到中值。只是

这样就牺牲了内存空间。

下面是算法具体实现步骤与代码：

　　1.扩展图像边界，上边界扩展r+1行，其他边界扩展r行；为每列生成两层直方图，并为其初始化，添加各列的前2*r+1个像素；生成一个低层链接高层的索引矩阵。

　　2.每行开始清零核直方图，更新核覆盖的各列直方图（向下移动一行），将各列加到核直方图中。

　　3.寻找中值，初始化sumcnt=0，这里它表示小于等于中值灰度的像素和，从左到右迭代高层直方图，直到sumcnt大于等于阈值；再从高层确定的范围内从右到左迭代

　　　低层直方图，直到sumcnt（减去了迭代灰度的像素数）小于阈值，则当前迭代值为中值。

　　4.核每向右移动，更新列直方图与核直方图，执行一次步骤3，然后继续移动核，直到完成整个图的滤波。

function grayimg=medianfilterdp(grayimg,radius,percentage)
    [sizex,sizey]=size(grayimg);
    thres=int16(((*radius+)^*percentage));
    %扩展边界
    extendimg=int16(horzcat(repmat(grayimg(:,),,radius),grayimg,repmat(grayimg(:,sizey),,radius)));
    extendimg=int16(vertcat(repmat(extendimg(,:),radius+,),extendimg,repmat(extendimg(sizex,:),radius,)));
    %为每一列维护一个全位直方图和一个高位直方图
    histogram_cols_low=int16(zeros(sizey+*radius,));
    histogram_cols_high=int16(zeros(sizey+*radius,));
    %中值计算所用的一个全位直方图和一个高位直方图
    histogram_low=int16(zeros(,));
    histogram_high=int16(zeros(,));
    %全位转高位的加速索引
    grayrange=int16(zeros(,));
    for i=:
        grayrange(:,(i-)*+:i*)=i;
    end
    %初始化各列直方图
    for row=:*radius+
        for col=:sizey+*radius
            histogram_cols_low(col,extendimg(row,col)+)=histogram_cols_low(col,extendimg(row,col)+)+;
            histogram_cols_high(col,grayrange(extendimg(row,col)+))=histogram_cols_high(col,grayrange(extendimg(row,col)+))+;
        end
    end

    for row=int16(radius+:sizex+radius+)
        for col=int16(radius+:sizey+radius)
            if(col>radius+)
                %更新右边新列，删除左边旧列
                histogram_cols_low(col+radius,extendimg(row+radius,col+radius)+)=histogram_cols_low(col+radius,extendimg(row+radius,col+radius)+)+;
                histogram_cols_low(col+radius,extendimg(row-radius-,col+radius)+)=histogram_cols_low(col+radius,extendimg(row-radius-,col+radius)+)-;
                histogram_cols_high(col+radius,grayrange(extendimg(row+radius,col+radius)+))=histogram_cols_high(col+radius,grayrange(extendimg(row+radius,col+radius)+))+;
                histogram_cols_high(col+radius,grayrange(extendimg(row-radius-,col+radius)+))=histogram_cols_high(col+radius,grayrange(extendimg(row-radius-,col+radius)+))-;
                histogram_low=histogram_low+histogram_cols_low(col+radius,:)-histogram_cols_low(col-radius-,:);
                histogram_high=histogram_high+histogram_cols_high(col+radius,:)-histogram_cols_high(col-radius-,:);
            else
                histogram_low(:,:)=;
                histogram_high(:,:)=;
                %行首手动初始化各列
                for index=:*radius+
                    histogram_cols_low(index,extendimg(row+radius,index)+)=histogram_cols_low(index,extendimg(row+radius,index)+)+;
                    histogram_cols_low(index,extendimg(row-radius-,index)+)=histogram_cols_low(index,extendimg(row-radius-,index)+)-;
                    histogram_cols_high(index,grayrange(extendimg(row+radius,index)+))=histogram_cols_high(index,grayrange(extendimg(row+radius,index)+))+;
                    histogram_cols_high(index,grayrange(extendimg(row-radius-,index)+))=histogram_cols_high(index,grayrange(extendimg(row-radius-,index)+))-;
                    histogram_low=histogram_low+histogram_cols_low(index,:);
                    histogram_high=histogram_high+histogram_cols_high(index,:);
                end
            end
            %中值及之前的所有像素数
            sumcnt=int16();
            for gray_high=:
                sumcnt=sumcnt+histogram_high(gray_high);
                if (sumcnt>=thres)
                    break;
                end
            end

            for gray_low=gray_high*:-:(gray_high-)*+
                sumcnt=sumcnt-histogram_low(gray_low);
                if (sumcnt<thres)
                    break;
                end
            end

            grayimg(row-radius-,col-radius)=gray_low-;
        end
    end

end

O(1)中值滤波

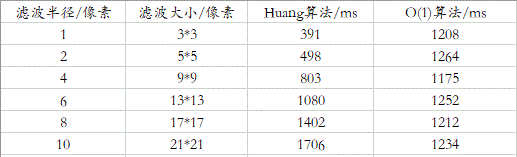
　　下面是两种算法的性能对比，可以发现，在滤波半径较小的时候，用Huang算法更好；当滤波半径>=8时，用后一种算法更快。实际中我们一般用不到大半径，但这两种

算法的思想很不错，尤其是第二种的空间换时间，我们可能可以发现横向存在重复性，但很容易忽略了纵向上的重复性。