Linear Algebra lecture 2 note

Lecture2

Elimination

Inverses

Permutation

---

消元法介绍（elimination）：

有方程组

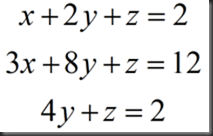
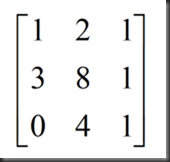
提取系数，形成矩阵为：

消元的思想跟解方程组中先消除未知数的思路一致，通过数乘(multiply)和减法(substract)化简,化简过程为：

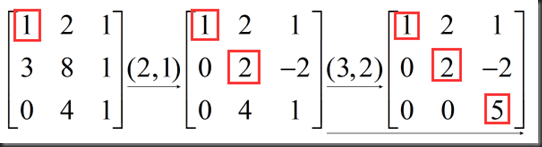
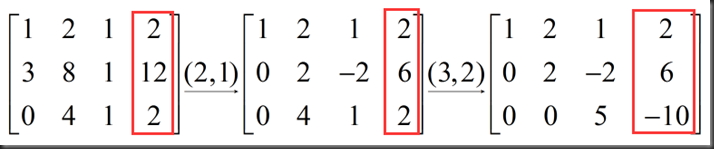
以上红框起来的数字叫pivot（主元），此例中主元分别为1、2、5

第一步操作是为了将第二行第一列的值变为0，简记为（2，1），即row2-3*row1，

由于第三行第一列的值已为0，下一步操作是为了将第三行第二列的值变为0，简记为（3，2），即row3-2*row2,

 

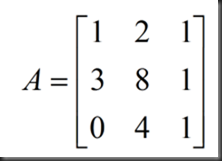
我们由A矩阵得到了U矩阵（U代表upper triangle,上三角矩阵）

教授提到一句：由此U矩阵可知行列式（determinant）为1*2*5=10（具体概念后面再讲）

若想求得正确的解，那么方程组右边的值也需要进行相同的变换，在原A矩阵右侧加一列，称为增广矩阵，进行相同变化的过程为：

下面我们进行回代，写回方程组的形式来看看：

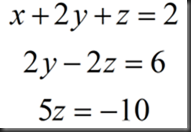
我们可以很容易解出，z=-2,y=1,x=2

---

对于矩阵右乘向量,结果以列的形式组合，matrix * colunm=columns combination

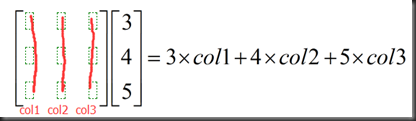
对于矩阵左乘向量，结果以行的形式组合，row * matrix = rows  combination

思考：如何通过乘以一个矩阵得到化简形式，将所乘矩阵称为初等矩阵，由于需要消除的是第二行第一列的值，记此初等矩阵E21，

求E21，视为combination of rows,第一行、第三行不变，第二行是取第一行的负三倍与原来的第二行加和而成，故可得：

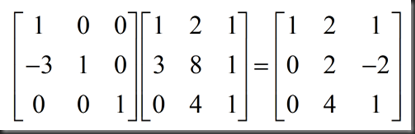
下一步，消除第三行第二列的值，记此初等矩阵E32，

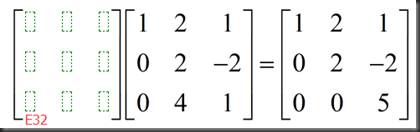
求E32,视为combination of rows,第一行、第二行不变，第三行是取此时第二行的负二倍与原第三行加和而成，故可得：

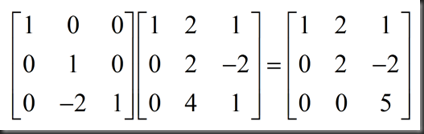
E32（E21A）=U

（E32E21）A=U

EA=U

---

Inverses（逆）

矩阵乘以初等矩阵相当于做了消元变换，将变换后的矩阵再恢复回去，视为逆作用，就需要乘以逆矩阵，可得单位矩阵，单位矩阵（Identity）记作I，乘以单位矩阵就相当于没有作用

---

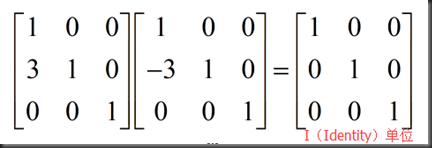
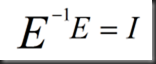
Permutation(置换）

Exchange rows

思考：如何通过乘以一个矩阵达到行交换的效果？

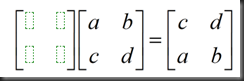
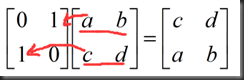
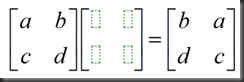
附加思考：如何通过乘以一个矩阵达到列交换的效果？