基于直接最小二乘的椭圆拟合（Direct Least Squares Fitting of Ellipses）

算法思想：

算法通过最小化约束条件4ac-b^2 = 1，最小化距离误差。利用最小二乘法进行求解，首先引入拉格朗日乘子算法获得等式组，然后求解等式组得到最优的拟合椭圆。

算法的优点：

　　a、椭圆的特异性，在任何噪声或者遮挡的情况下都会给出一个有用的结果；

　　b、不变性，对数据的Euclidean变换具有不变性，即数据进行一系列的Euclidean变换也不会导致拟合结果的不同；

　　c、对噪声具有很高的鲁棒性；

　　d、计算高效性。

算法原理：

代码实现（Matlab）：

 %
 function a = fitellipse(X,Y)

 % FITELLIPSE  Least-squares fit of ellipse to 2D points.
 %        A = FITELLIPSE(X,Y) returns the parameters of the best-fit
 %        ellipse to 2D points (X,Y).
 %        The returned vector A contains the center, radii, and orientation
 %        of the ellipse, stored as (Cx, Cy, Rx, Ry, theta_radians)
 %
 % Authors: Andrew Fitzgibbon, Maurizio Pilu, Bob Fisher
 % Reference: "Direct Least Squares Fitting of Ellipses", IEEE T-PAMI,
 %
 %  @Article{Fitzgibbon99,
 %   author = "Fitzgibbon, A.~W.and Pilu, M. and Fisher, R.~B.",
 %   title = "Direct least-squares fitting of ellipses",
 %   journal = pami,
 %   year = 1999,
 %   volume = 21,
 %   number = 5,
 %   month = may,
 %   pages = "476--480"
 %  }
 %
 % This is a more bulletproof version than that in the paper, incorporating
 % scaling to reduce roundoff error, correction of behaviour when the input
 % data are on a perfect hyperbola, and returns the geometric parameters
 % of the ellipse, rather than the coefficients of the quadratic form.
 %
 %  Example:  Run fitellipse without any arguments to get a demo
 if nargin ==
   % Create an ellipse
   t = linspace(,);

   Rx = ;
   Ry = ;
   Cx = ;
   Cy = ;
   Rotation = .; % Radians

   NoiseLevel = .; % Will add Gaussian noise of this std.dev. to points

   x = Rx * cos(t);
   y = Ry * sin(t);
   nx = x*cos(Rotation)-y*sin(Rotation) + Cx + randn(size(t))*NoiseLevel;
   ny = x*sin(Rotation)+y*cos(Rotation) + Cy + randn(size(t))*NoiseLevel;

   % Clear figure
   clf
   % Draw it
   plot(nx,ny,'o');
   % Show the window
   figure(gcf)
   % Fit it
   params = fitellipse(nx,ny);
   % Note it may return (Rotation - pi/) and swapped radii, this is fine.
   Given = round([Cx Cy Rx Ry Rotation*])
   Returned = round(params.*[    ])

   % Draw the returned ellipse
   t = linspace(,pi*);
   x = params() * cos(t);
   y = params() * sin(t);
   nx = x*cos(params())-y*sin(params()) + params();
   ny = x*sin(params())+y*cos(params()) + params();
   hold on
   plot(nx,ny,'r-')

   return
 end

 % normalize data
 mx = mean(X);
 my = mean(Y);
 sx = (max(X)-min(X))/;
 sy = (max(Y)-min(Y))/; 

 x = (X-mx)/sx;
 y = (Y-my)/sy;

 % Force to column vectors
 x = x(:);
 y = y(:);

 % Build design matrix
 D = [ x.*x  x.*y  y.*y  x  y  ones(size(x)) ];

 % Build scatter matrix
 S = D'*D;

 % Build 6x6 constraint matrix
 C(,) = ; C(,) = -; C(,) = ; C(,) = -;

 % Solve eigensystem
 if
   % Old way, numerically unstable if not implemented in matlab
   [gevec, geval] = eig(S,C);

   % Find the negative eigenvalue
   I = find(real(diag(geval)) < 1e-8 & ~isinf(diag(geval)));

   % Extract eigenvector corresponding to negative eigenvalue
   A = real(gevec(:,I));
 else
   % New way, numerically stabler in C [gevec, geval] = eig(S,C);

   % Break into blocks
   tmpA = S(:,:);
   tmpB = S(:,:);
   tmpC = S(:,:);
   tmpD = C(:,:);
   tmpE = inv(tmpC)*tmpB';
   [evec_x, eval_x] = eig(inv(tmpD) * (tmpA - tmpB*tmpE));

   % Find the positive (as det(tmpD) < ) eigenvalue
   I = find(real(diag(eval_x)) < 1e-8 & ~isinf(diag(eval_x)));

   % Extract eigenvector corresponding to negative eigenvalue
   A = real(evec_x(:,I));

   % Recover the bottom half...
   evec_y = -tmpE * A;
   A = [A; evec_y];
 end

 % unnormalize
 par = [
   A()*sy*sy,   ...
       A()*sx*sy,   ...
       A()*sx*sx,   ...
       -*A()*sy*sy*mx - A()*sx*sy*my + A()*sx*sy*sy,   ...
       -A()*sx*sy*mx - *A()*sx*sx*my + A()*sx*sx*sy,   ...
       A()*sy*sy*mx*mx + A()*sx*sy*mx*my + A()*sx*sx*my*my   ...
       - A()*sx*sy*sy*mx - A()*sx*sx*sy*my   ...
       + A()*sx*sx*sy*sy   ...
       ]';

 % Convert to geometric radii, and centers

 thetarad = 0.5*atan2(par(),par() - par());
 cost = cos(thetarad);
 sint = sin(thetarad);
 sin_squared = sint.*sint;
 cos_squared = cost.*cost;
 cos_sin = sint .* cost;

 Ao = par();
 Au =   par() .* cost + par() .* sint;
 Av = - par() .* sint + par() .* cost;
 Auu = par() .* cos_squared + par() .* sin_squared + par() .* cos_sin;
 Avv = par() .* sin_squared + par() .* cos_squared - par() .* cos_sin;

 % ROTATED = [Ao Au Av Auu Avv]

 tuCentre = - Au./(.*Auu);
 tvCentre = - Av./(.*Avv);
 wCentre = Ao - Auu.*tuCentre.*tuCentre - Avv.*tvCentre.*tvCentre;

 uCentre = tuCentre .* cost - tvCentre .* sint;
 vCentre = tuCentre .* sint + tvCentre .* cost;

 Ru = -wCentre./Auu;
 Rv = -wCentre./Avv;

 Ru = sqrt(abs(Ru)).*sign(Ru);
 Rv = sqrt(abs(Rv)).*sign(Rv);

 a = [uCentre, vCentre, Ru, Rv, thetarad];

实验效果：

a、同等噪声条件下，不同长度的样本点，导致的拟合结果，如下所示：

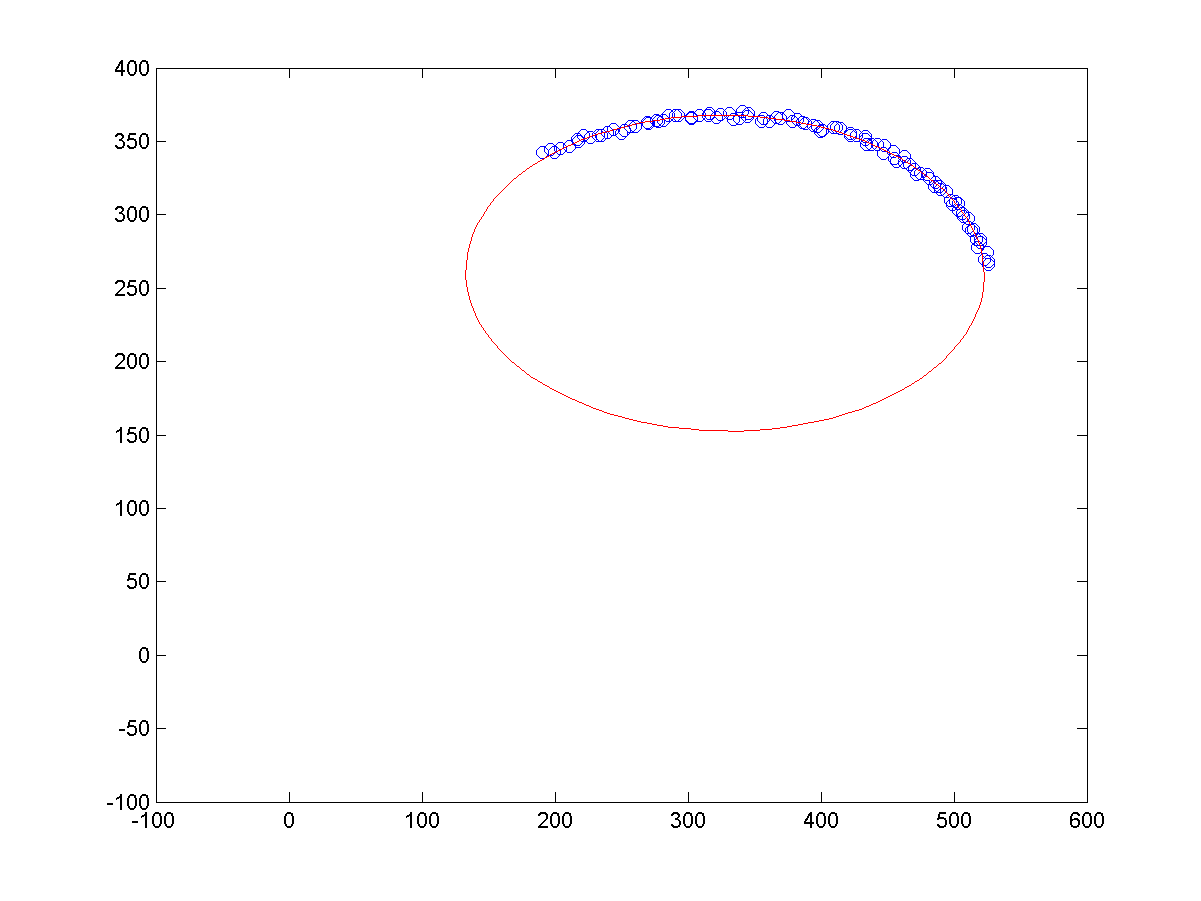
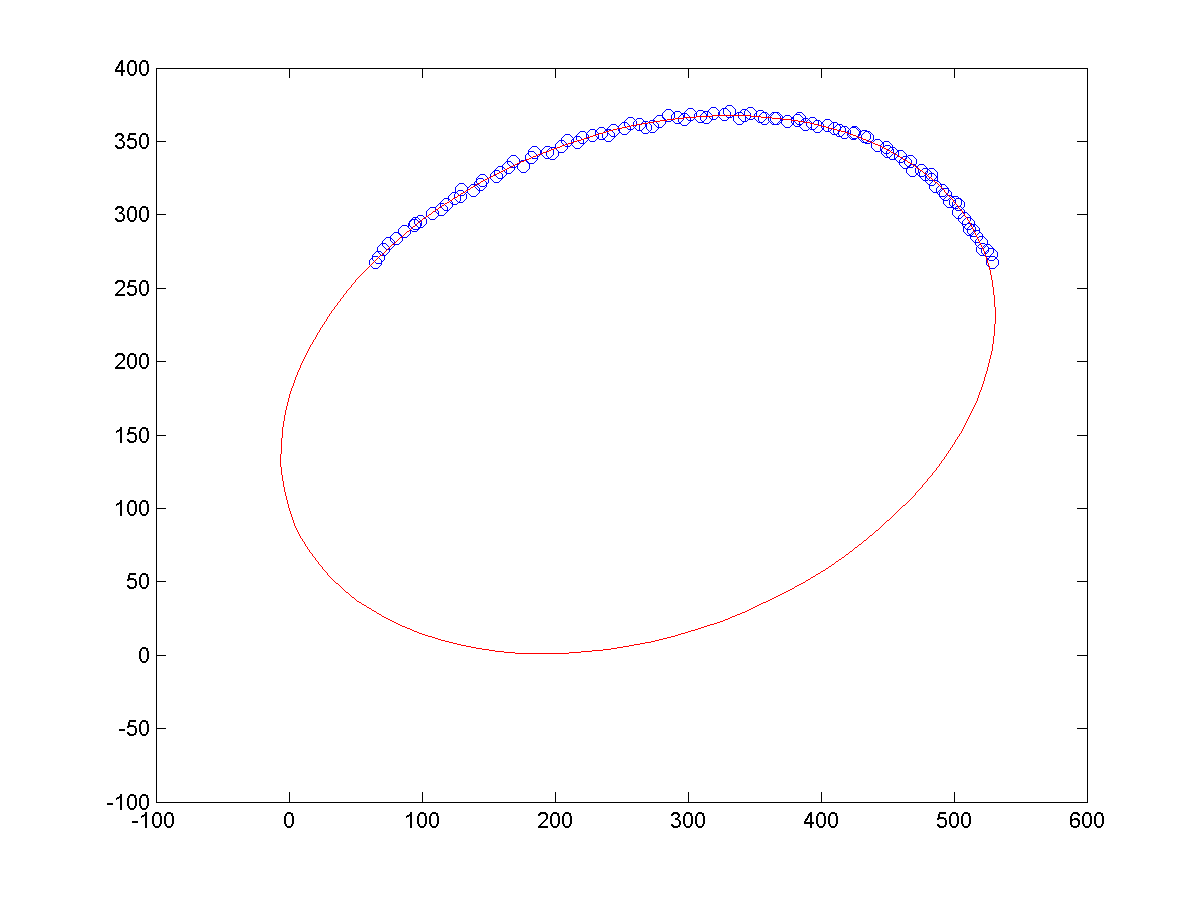
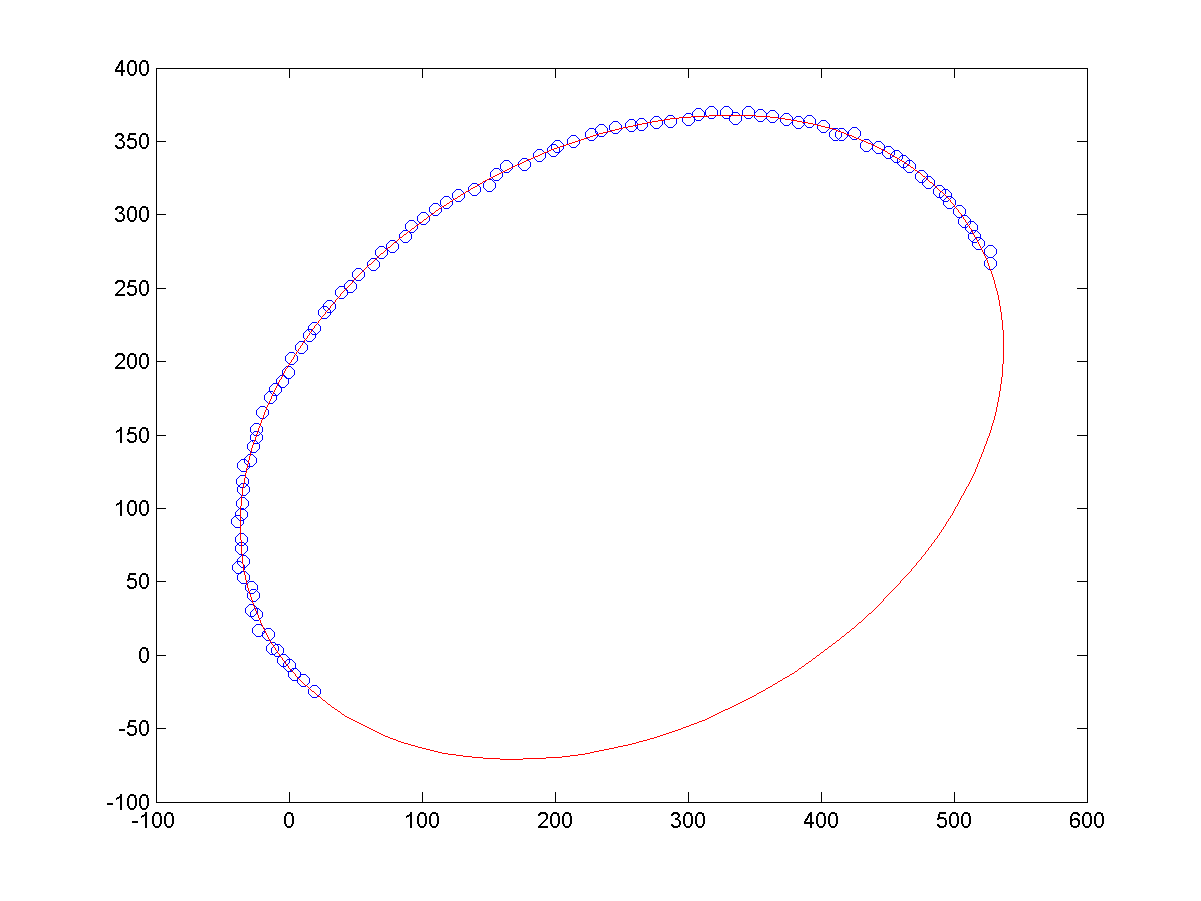
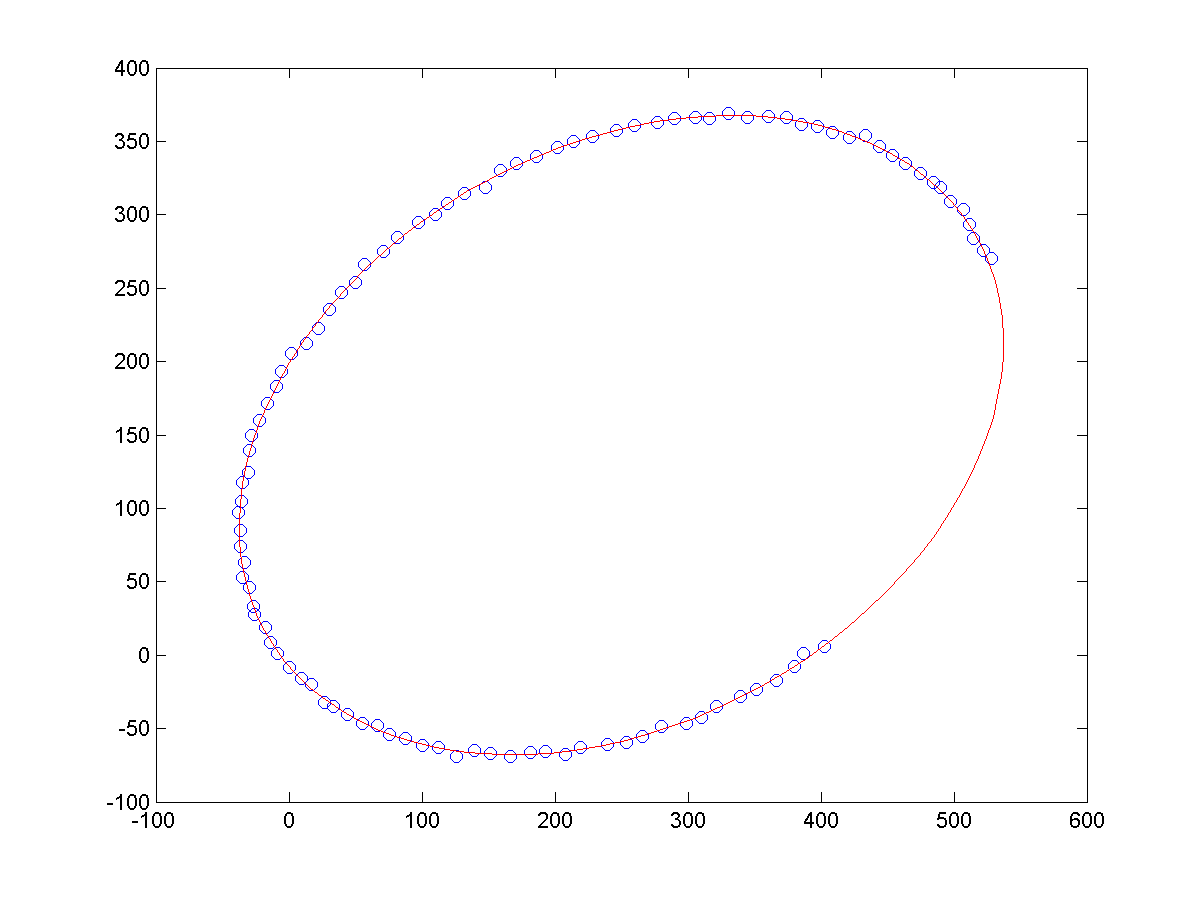
b、相同长度的样本点下，不同噪声的样本点，导致的拟合结果，如下所示：

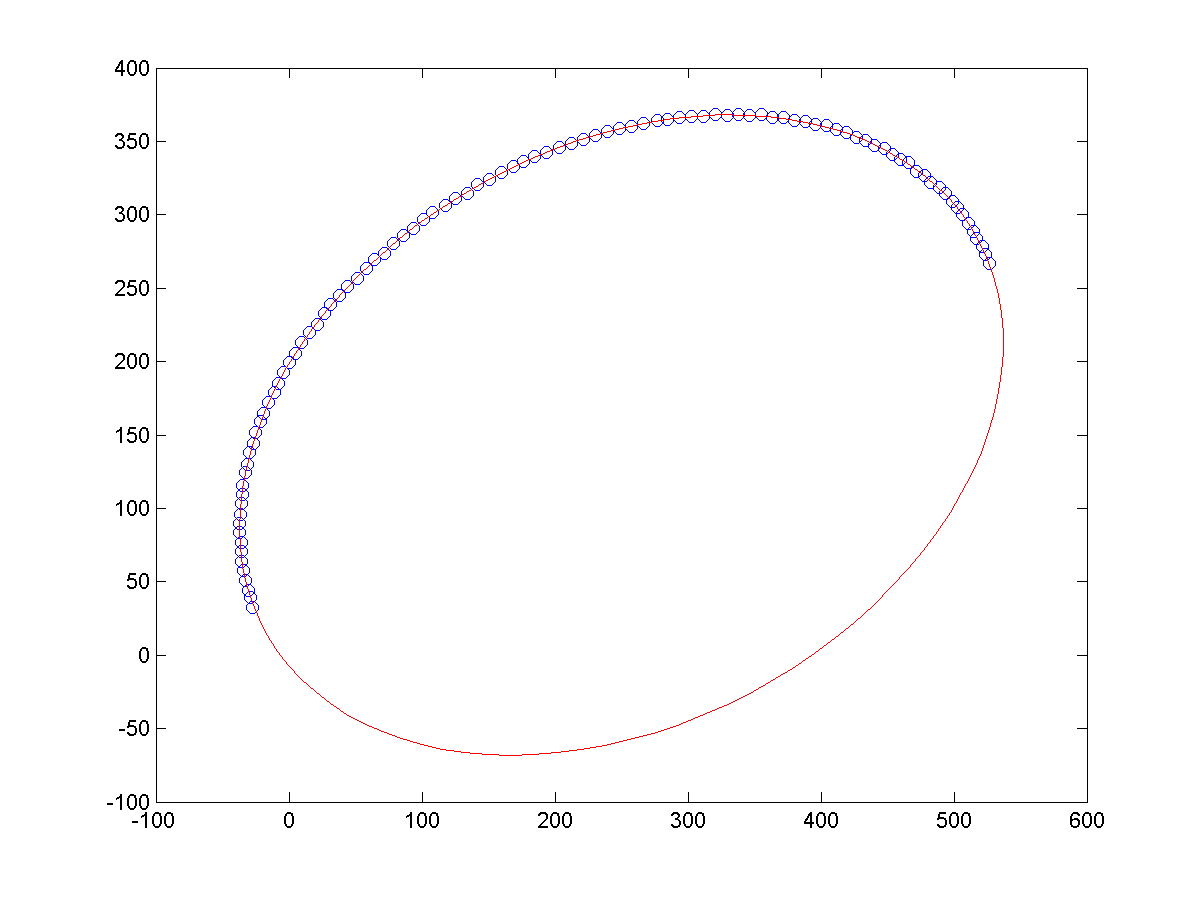
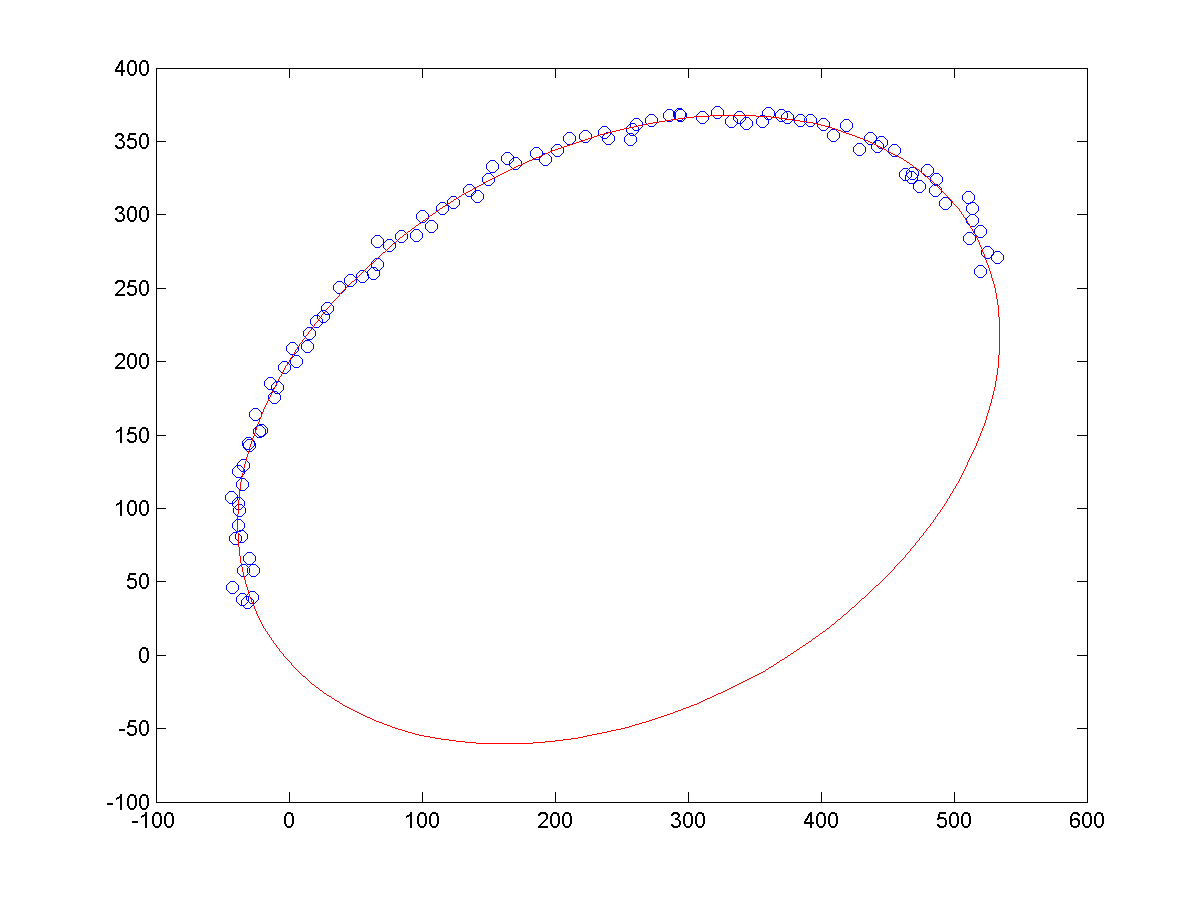
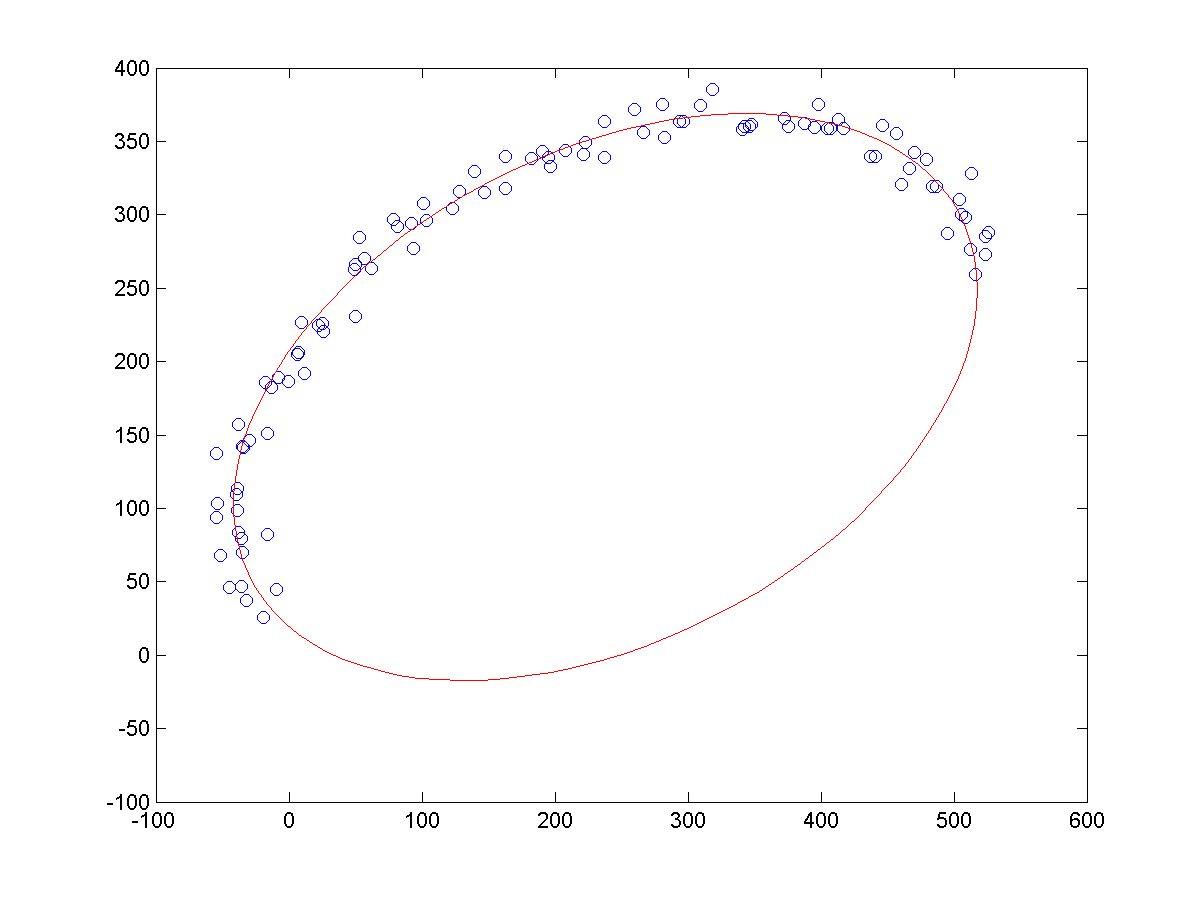
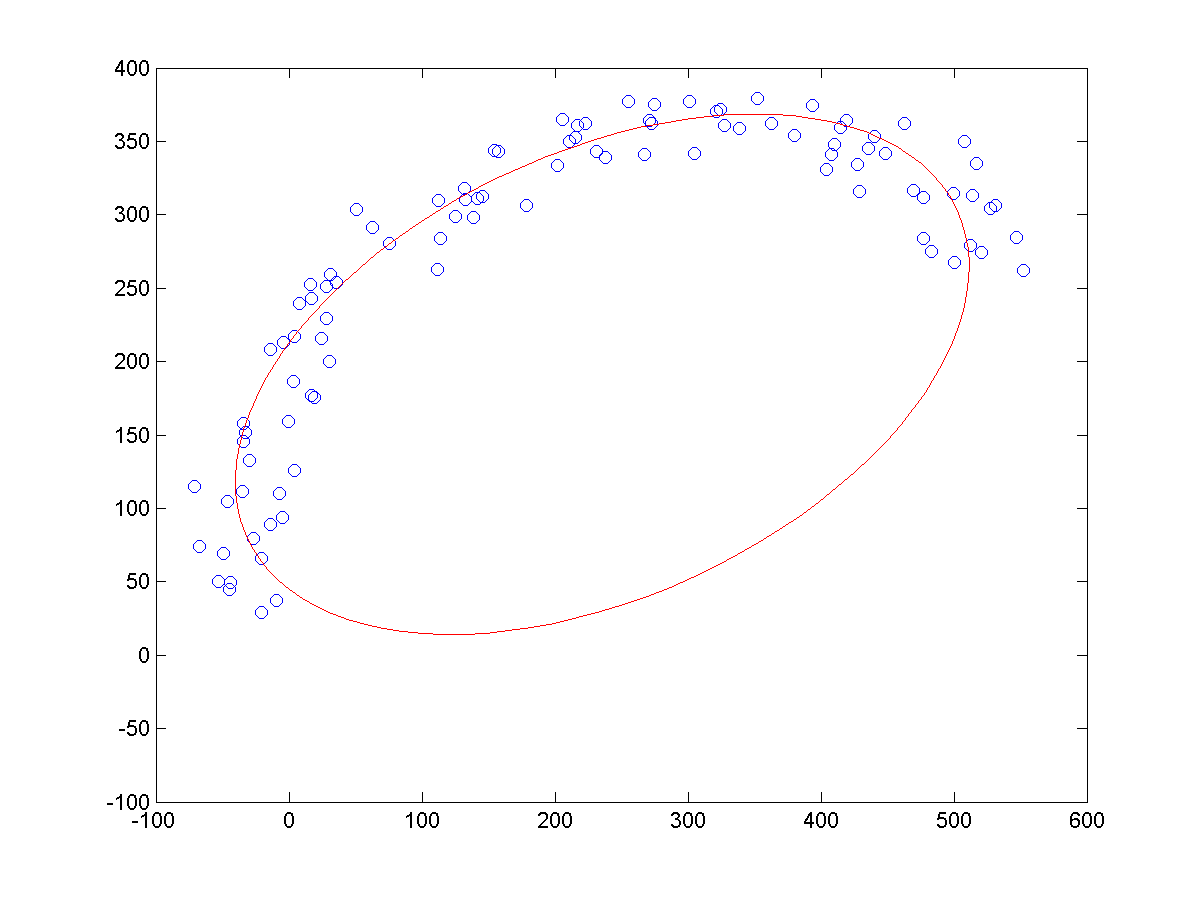
c、少样本点下，拟合结果如下：

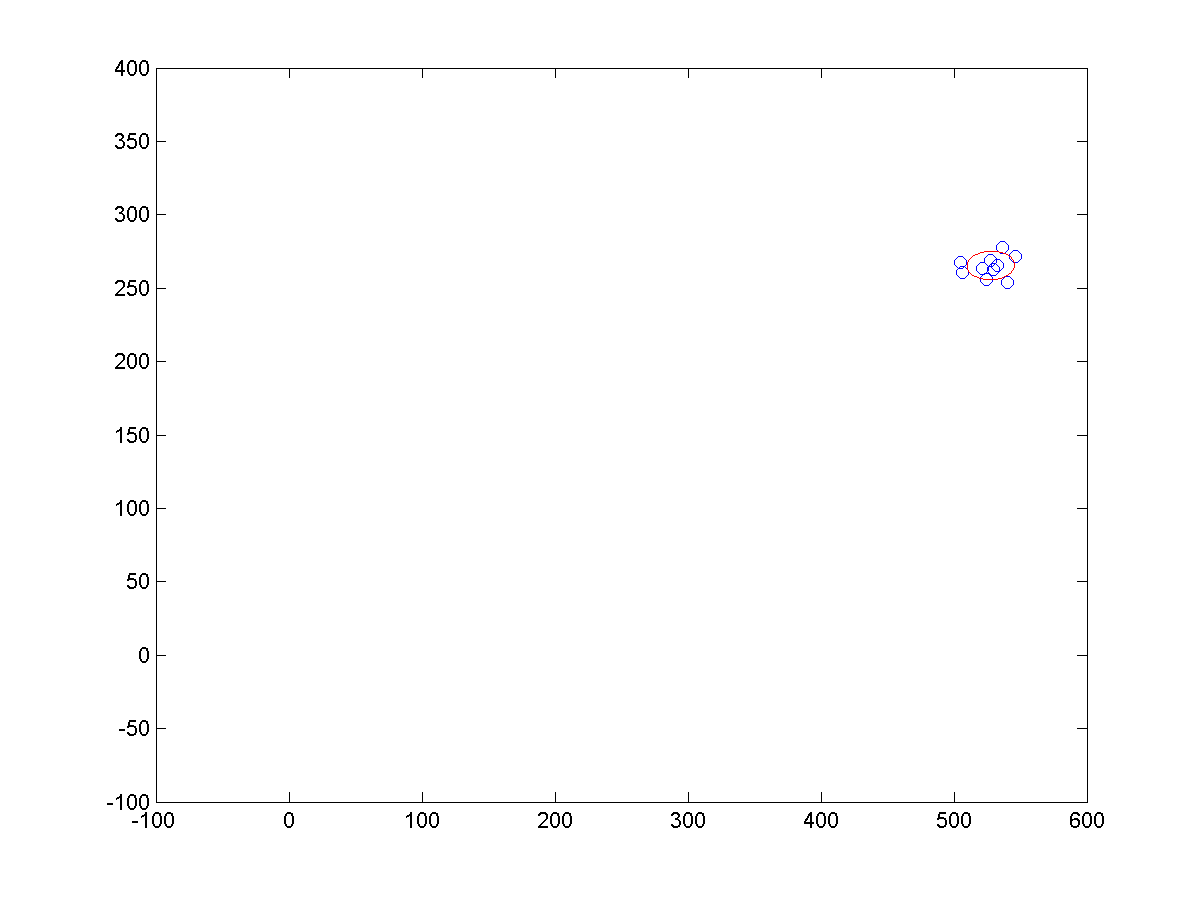
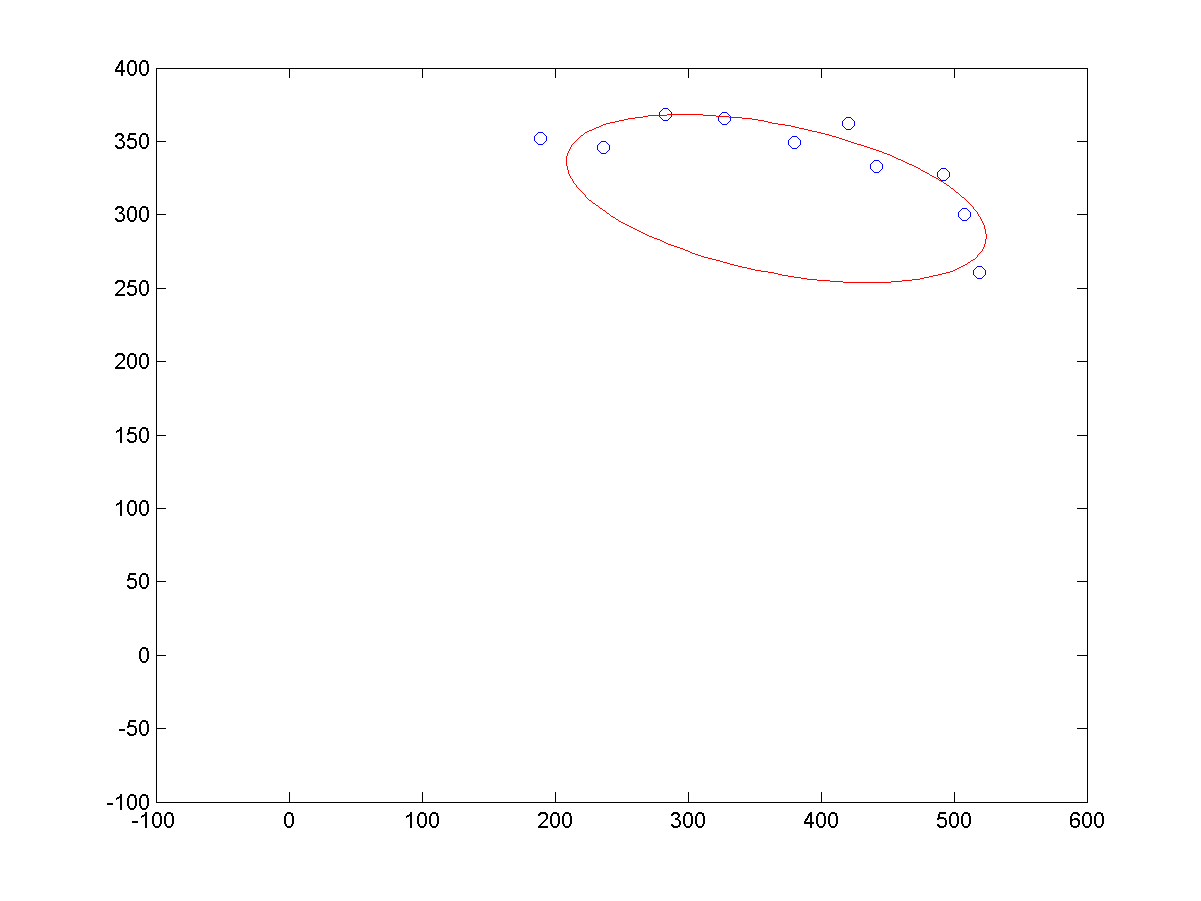
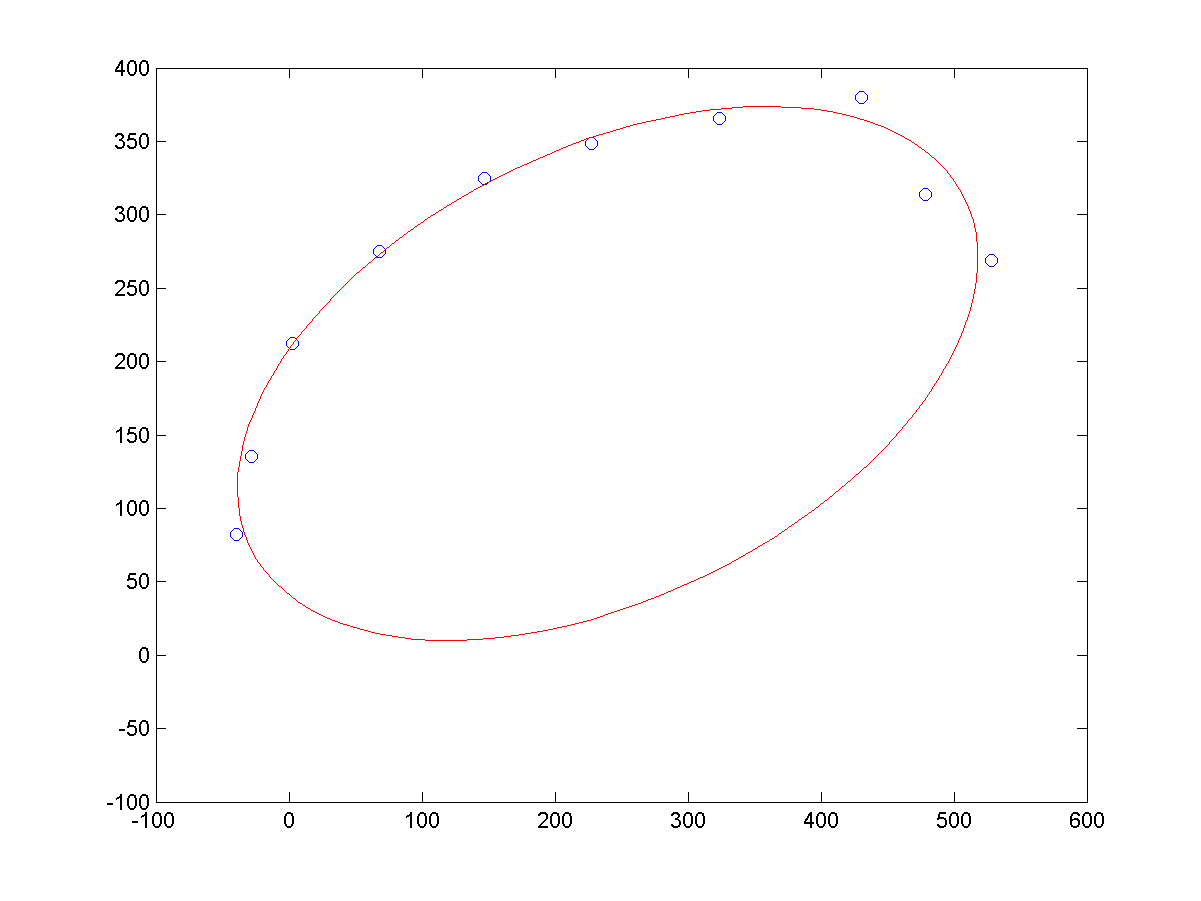
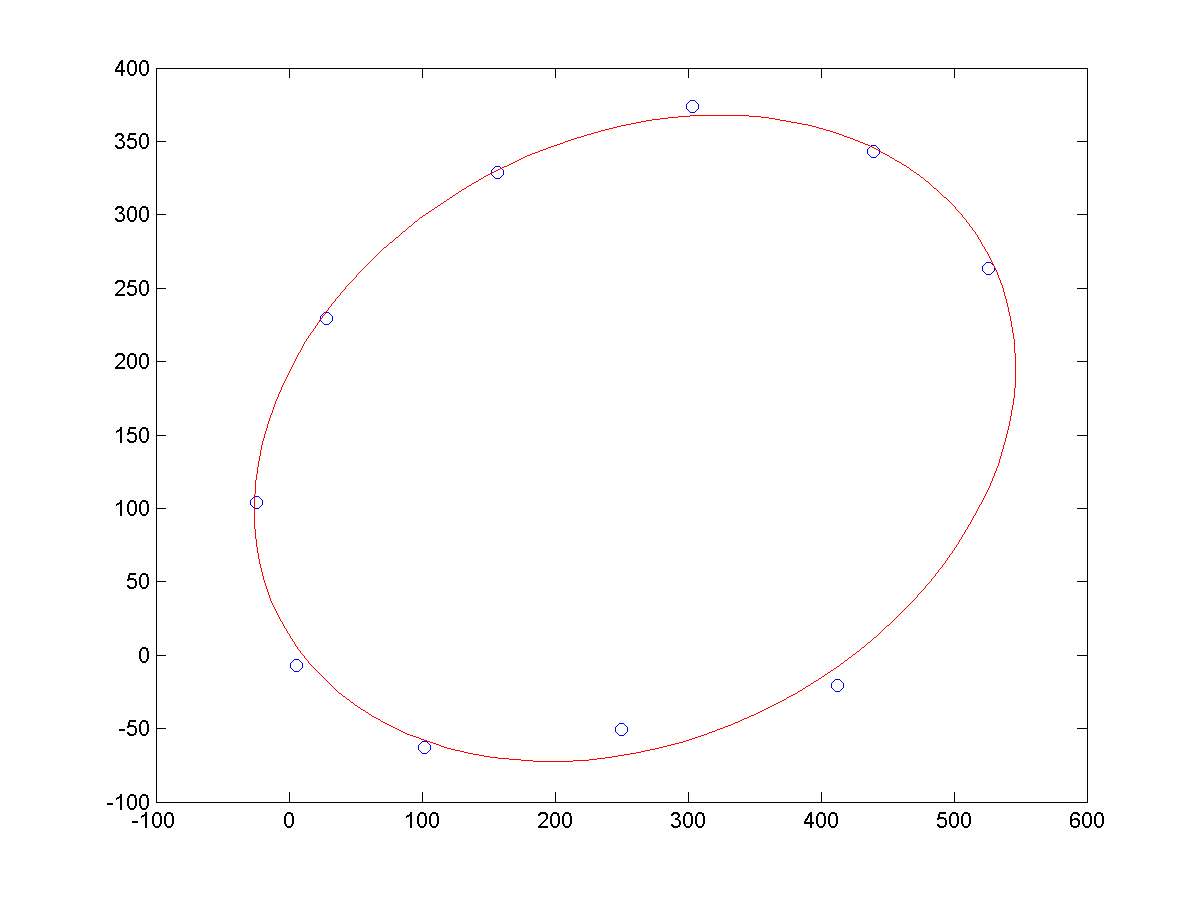
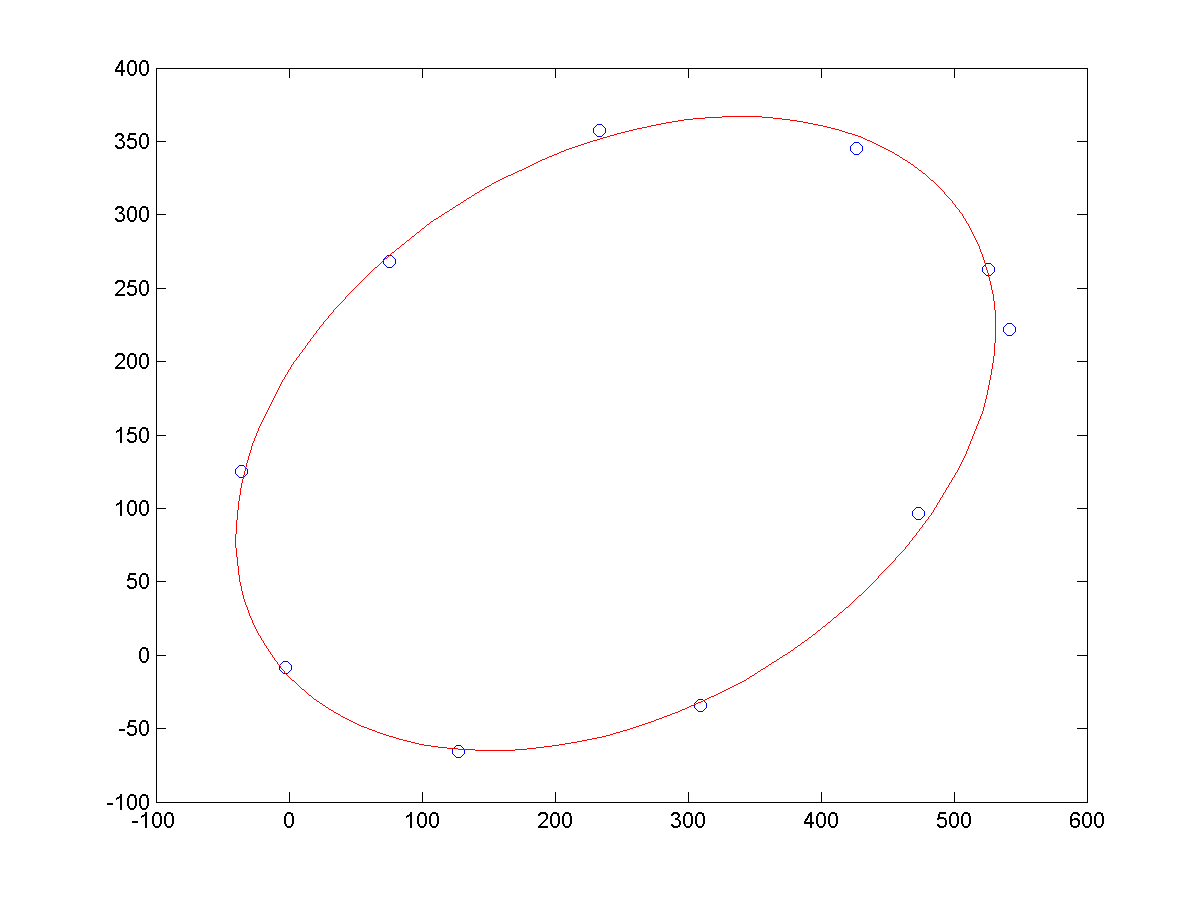
源码下载：

      地址： FitEllipse

参考文献：

[1]. Andrew W. Fitzgibbon, Maurizio Pilu and Robert B. Fisher. Direct Least Squares Fitting of Ellipses. 1996.

[2]. http://research.microsoft.com/en-us/um/people/awf/ellipse/