基尼系数（Gini coefficient）,洛伦茨系数

20世纪初意大利经济学家基尼，于1922年提出的定量测定收入分配差异程度的指标。它是根据洛伦茨曲线找出了判断分配平等程度的指标（如下图）。

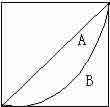
　　设实际收入分配曲线和收入分配绝对平等曲线之间的面积为A，实际收入分配曲线右下方的面积为B。并以A除以A+B的商表示不平等程度。这个数值被称为基尼系数或称洛伦茨系数。如果A为零，基尼系数为零，表示收入分配完全平等；如果B为零则系数为1，收入分配绝对不平等。该系数可在零和1之间取任何值。收入分配越是趋向平等，洛伦茨曲线的弧度越小，基尼系数也越小，反之，收入分配越是趋向不平等，洛伦茨曲线的弧度越大，那么基尼系数也越大。如果个人所得税能使收入均等化，那么，基尼系数即会变小。

　　基尼系数的计算公式为：

　　

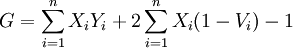
　　其中，X代表各组的人口比重，Y代表各组的收入比重，V代表各组累计的收入比重，i=1，2，3，…，n，n代表分组的组数。

___________________________________________________

基尼系数，按照联合国有关组织规定：

• 若低于0.2表示收入绝对平均；

• 0.2-0.3表示比较平均；

• 0.3-0.4表示相对合理；

• 0.4-0.5表示收入差距较大；

• 0.5以上表示收入差距悬殊。

　　经济学家们通常用基尼指数来表现一个国家和地区的财富分配状况。这个指数在零和一之间，数值越低，表明财富在社会成员之间的分配越均匀；反之亦然。

　　通常把0.4作为收入分配差距的“警戒线”。一般发达国家的基尼指数在0.24到0.36之间，美国偏高，为0.4。中国大陆和香港的基尼系数都超出0.4。

　　此外洛伦茨曲线讲的是市场总发货值的百分比与市场中由小到大厂商的累积百分比之间的关系。 洛伦茨曲线的弧度越小,基尼系数也越小。

_____________________________________________________________

基尼系数是联合国规定的用来衡量各个国家、地区、种族和行业收入分配不均等程度的统计指标，也是许多国家乃至我国大多数学者评判收入分配的最重要的依据。它的优点是可以利用简单的分组数据简练地概括洛伦兹曲线所描述的居民收入分配状况，以一个数值反映总体收入差距状况。但也正因为这种概括又使得它丢掉了洛伦兹曲线所表示的一些信息，在衡量和说明收入分配状况时存在一些不足。

　　基尼系数不能准确地反映洛伦兹曲线的形状，从而它不能精确地反映收入分配的不均等程度。由基尼系数的计算公式可知：基尼系数的值完全取决于洛伦兹曲线与绝对平均线之间的面积的大小，从数值无法知道各个收入阶层的收入结构，而对应不同的洛伦兹曲线，这块面积可能是相同的，即有相同的基尼系数。

　　现举例说明，见下表。此例中，情况1、情况2的洛伦兹曲线分别见下图中曲线L1、L2。如下图所示，L1与L2所表示的收入分配结构显然不同，情况2的洛伦兹曲线比情况1的洛伦兹曲线偏向上，L1中的低收入群体相对贫困程度要远远高于L2所对应的分配结构，如果从扩大内需和保证社会稳定的角度出发，对于L1所描述的情形采取调整收入结构的政策措施，从而增加低收入阶层的收入水平更为迫切。但根据基尼系数的定义，由这两条曲线所计算出来的基尼系数是相等的，如果仅依据基尼系数，政策制定者就无法作出最为合理的决策。对此问题，Wilson(1987)曾经作过比较深入的研究。他通过对美国有关资料研究后发现，由于在黑人与白人间收入差异进一步扩大的同时，黑人家庭之间收入水平出现了趋同，实际计算的基尼系数却是缩小的，此时的基尼系数可能低估了美国居民的贫富差异程度。他进一步指出之所以出现这种结果，正是由于与基尼系数所对应的洛伦兹曲线的非唯一性，因而，用基尼系数反映贫富差距不够准确，至少是不够全面的。社会分配的不均等程度是由两种收入分配间的差距造成的，一种是由收入低于整个社会的平均收入而形成的差距；另一种是由收入高于整个社会的平均收入而形成的差距。基尼系数计算的是这两种差距的总和，但不能反映出这两种差距各自的大小程度。

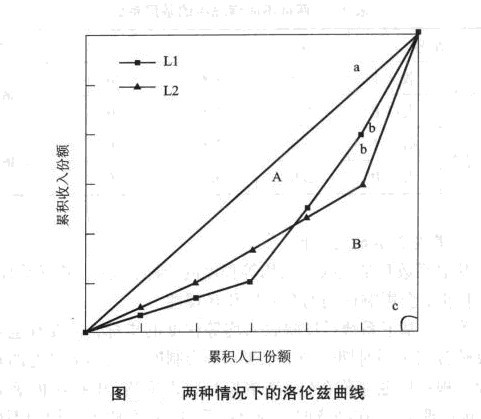两种不同情况中的基尼系数

组号		1	2	3	基尼系数
情况1	收入I	1／6	3／6	2／6	13／36
	人口P	3／6	2／6	1／6
情况2	收入I	1／6	2／6	3／6	13／36
	人口P	2／6	3／6	1／6

__________________________________________

劳伦茨曲线是1905年由经济学家马克斯·劳伦茨所提出的表示收入分配的曲线，意大利经济学家科拉多·基尼在此基础上定义了基尼系数。

在经济学里，劳伦兹曲线是在过往财富分配数据上建立的累积分布函数所对应的曲线，它通过变量y%的值来反映各项分配的比例。它经常被用来描述收入的分配情况，即以x%代表一部分（收入相似）家庭占整个社会家庭的比例，以y%代表该部分家庭的收入占整个社会收入的比例。该曲线也可用来描述社会资本的分配情况。在这些应用当中，经济学家经常把它用来衡量社会（主要指社会收入）是否公平。概率密度函数（f(x)）或累积分布函数（F(x)）：

L ( F ) = ∫ − ∞ x ( F ) x f ( x ) d x ∫ − ∞ ∞ x f ( x ) d x = ∫ 0 F x ( F ′ ) d F ′ ∫ 0 1 x ( F ′ ) d F ′ {\displaystyle L(F)={\frac {\int _{-\infty }^{x(F)}xf(x)\,dx}{\int _{-\infty }^{\infty }xf(x)\,dx}}={\frac {\int _{0}^{F}x(F')\,dF'}{\int _{0}^{1}x(F')\,dF'}}}

这曲线在发展经济学上，除了用于常见的基尼系数表示收入分布，还有土地分布，教育度的程度的分布等。

____________________________________________________________

画一个矩形，矩形的高衡量社会财富的百分比，将之分为五等份，每一等分为20的社会总财富。在矩形的长上，将100的家庭从最贫者到最富者自左向右排列，也分为5等分，第一个等份代表收入最低的20的家庭。在这个矩形中，将每一百分的家庭所有拥有的财富的百分比累计起来，并将相应的点画在图中，便得到了一条曲线就是洛伦兹曲线。

　　

　　 显而易见，洛伦兹曲线的弯曲程度具有重要意义。一般来说，它反映了收入分配的不平等程度。弯曲程度越大，收入分配程度越不平等；反之亦然。特别是，如果所有收入都集中在某一个人手中，而其余人口均一无所有，收入分配达到完全不平等，洛伦兹曲线成为折线OHL；另一方面，如果任一人口百分比等于其收入百分比，从而人口累计百分比等于收入累计百分比，则收入分配就是完全平等的，洛伦兹曲线成为通过原点的45度线OL。

\