Codeforces 689B. Mike and Shortcuts SPFA/搜索

B. Mike and Shortcuts

time limit per test：

3 seconds

memory limit per test:

256 megabytes

input：

standard input

output：

standard output

Recently, Mike was very busy with studying for exams and contests. Now he is going to chill a bit by doing some sight seeing in the city.

City consists of n intersections numbered from 1 to n. Mike starts walking from his house located at the intersection number 1 and goes along some sequence of intersections. Walking from intersection number i to intersection j requires |i - j| units of energy. The total energy spent by Mike to visit a sequence of intersections p1 = 1, p2, ..., pk is equal to  units of energy.

Of course, walking would be boring if there were no shortcuts. A shortcut is a special path that allows Mike walking from one intersection to another requiring only 1 unit of energy. There are exactly n shortcuts in Mike's city, the ith of them allows walking from intersection i to intersection ai (i ≤ ai ≤ ai + 1) (but not in the opposite direction), thus there is exactly one shortcut starting at each intersection. Formally, if Mike chooses a sequence p1 = 1, p2, ..., pk then for each 1 ≤ i < k satisfying pi + 1 = api and api ≠ pi Mike will spend only 1 unit of energy instead of |pi - pi + 1| walking from the intersection pi to intersection pi + 1. For example, if Mike chooses a sequencep1 = 1, p2 = ap1, p3 = ap2, ..., pk = apk - 1, he spends exactly k - 1 units of total energy walking around them.

Before going on his adventure, Mike asks you to find the minimum amount of energy required to reach each of the intersections from his home. Formally, for each 1 ≤ i ≤ n Mike is interested in finding minimum possible total energy of some sequence p1 = 1, p2, ..., pk = i.

Input

The first line contains an integer n (1 ≤ n ≤ 200 000) — the number of Mike's city intersection.

The second line contains n integers a1, a2, ..., an (i ≤ ai ≤ n , 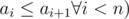, describing shortcuts of Mike's city, allowing to walk from intersection i to intersection ai using only 1 unit of energy. Please note that the shortcuts don't allow walking in opposite directions (from ai to i).

Output

In the only line print n integers m1, m2, ..., mn, where mi denotes the least amount of total energy required to walk from intersection 1 to intersection i.

Examples

input

3
2 2 3

output

0 1 2 

input

5
1 2 3 4 5

output

0 1 2 3 4 

input

7
4 4 4 4 7 7 7

output

0 1 2 1 2 3 3 

Note

In the first sample case desired sequences are:

1: 1; m1 = 0;

2: 1, 2; m2 = 1;

3: 1, 3; m3 = |3 - 1| = 2.

In the second sample case the sequence for any intersection 1 < i is always 1, i and mi = |1 - i|.

In the third sample case — consider the following intersection sequences:

1: 1; m1 = 0;

2: 1, 2; m2 = |2 - 1| = 1;

3: 1, 4, 3; m3 = 1 + |4 - 3| = 2;

4: 1, 4; m4 = 1;

5: 1, 4, 5; m5 = 1 + |4 - 5| = 2;

6: 1, 4, 6; m6 = 1 + |4 - 6| = 3;

7: 1, 4, 5, 7; m7 = 1 + |4 - 5| + 1 = 3.

题目链接：http://codeforces.com/contest/689/problem/B

---

题意：任意两点的距离为两点序号差的绝对值，有一些特殊的点，i到ai的距离为1.求1到每个点的最短距离。

思路：SPFA模板题。任意两个编号相邻的点的距离为1构造双向边，再加上n个特殊点构成的边。因为n最大为200000，套用SPFA模板。

代码：

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 6e5+, mod = 1e9 + , inf = 0x3f3f3f3f;
struct node
{
    int to,d;
} edge[*MAXN];
int head[MAXN],nextt[*MAXN];
int sign[MAXN];
queue<int>Q;
int dist[MAXN];
int n;
void add(int i,int u,int v,int d)
{
    edge[i].to=v;
    edge[i].d=d;
    nextt[i]=head[u];
    head[u]=i;
}
void SPFA(int v)
{
    int i,u;
    for(i=; i<=n; i++)
    {
        dist[i]=inf;
        sign[i]=;
    }
    dist[v]=;
    Q.push(v);
    sign[v]=;
    while(!Q.empty())
    {
        u=Q.front();
        Q.pop();
        sign[u]=;
        i=head[u];
        while(i!=)
        {
            if(dist[edge[i].to]>dist[u]+edge[i].d)
            {
                dist[edge[i].to]=dist[u]+edge[i].d;
                if(!sign[edge[i].to])
                {
                    Q.push(edge[i].to);
                    sign[edge[i].to]=;
                }
            }
            i=nextt[i];
        }
    }
}
int a[];
int main()
{
    int i,j;
    scanf("%d",&n);
    memset(head,,sizeof(head));
    j=;
    for(i=; i<=n; i++)
    {
        scanf("%d",&a[i]);
        if(i!=a[i]) add(j++,i,a[i],);
        if(i>)
        {
            add(j++,i-,i,);
            add(j++,i,i-,);
        }
    }
    SPFA();
    for(i=; i<=n; i++)
        cout<<dist[i]<<" ";
    cout<<endl;
    return ;
}

SPFA

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 6e5+, mod = 1e9 + , inf = 0x3f3f3f3f;
vector<int>V[];
int dist[];
void DFS(int u)
{
    int i;
    for(i=; i<V[u].size(); i++)
    {
        if(dist[V[u][i]]>dist[u]+)
        {
            dist[V[u][i]]=dist[u]+;
            DFS(V[u][i]);
        }
    }
}
int main()
{
    int i,n,a;
    scanf("%d",&n);
    for(i=; i<=n; i++)
    {
        scanf("%d",&a);
        V[i].push_back(a);
        if(i+<=n) V[i].push_back(i+);
        if(i->=) V[i].push_back(i-);
    }
    for(i=; i<=n; i++) dist[i]=inf;
    dist[]=;
    DFS();
    for(i=;i<=n;i++)
        cout<<dist[i]<<" ";
    cout<<endl;
    return ;
}

DFS