51nod 1353 树 | 树形DP经典题！

51nod 1353 树 | 树形DP好题！

题面

切断一棵树的任意条边，这棵树会变成一棵森林。

现要求森林中每棵树的节点个数不小于k，求有多少种切法。

数据范围：\(n \le 2000\)。

题解

//为什么这道题做的人这么少呢……感觉这道题超级经典，非常符合上周末模拟那种树形DP的套路。会做这道题之后，可以想出许多类似的树形DP。

首先状态很好想：\(dp[u][i]\)表示“以u为根的子树中，与u相连的联通块大小是i，剩下的联通块大小均大于k”的方案数。

下面的题解中，我们设要求的是\(dp[u][i]\)，父亲是u，儿子是v，sze[i]表示以i为根的子树的大小。

为了方便起见，我们画图说明：

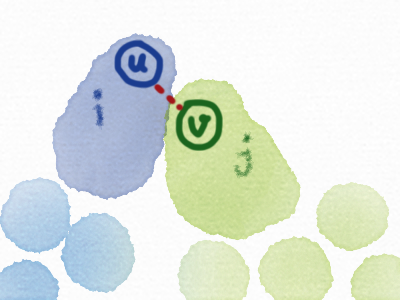
由于u有许多儿子，我们一次只处理一个儿子，处理的时候，就相当于将一堆新的节点（子树v）添加到原有的图。

现在与u相连的联通块大小为i，与j相连的大小为j。显然对于(u, v)之间的这条边，要么切断，要么不切断。上图描述的是切断的情况（这种情况要求j >= k)。显然新的\(dp[u][i] += dp[u][i] * dp[v][j]\)。（注意，等式右边的\(dp[u][i]\)是在联通块中加入子树v之前的答案）。

另一种情况是不切断这条边。如下图：

由于没切断，加入新子树之后，与u相连的联通块的大小由i变成了i + j。

那么显然：\(dp[u][i + j] += dp[u][i] * dp[v][j]\)。（等式右边的dp[u][i]仍是加入子树之前的）。

现在我们连状态转移方程都想好了，写代码是不是就很简单了呢？可能……并不是……（至少对于我来说）

十分需要注意的地方是\(dp[u][i]\)意义的变化。我们必须保证等式右边的\(dp[u][i]\)永远是加入子树之前的答案。例如，对于切断(u, v)这条边的情况，如果我们在u、v没有改变的情况下，直接这样循环:

for r i : 1 -> sze[u]
	for j : 1 -> sze[v]
		dp[u][i] += dp[u][i] * dp[v][j]

显然是不行的。因为等式右侧的\(dp[u][i]\)一经修改就不是“加入子树v之前的”了。

一种合理的解决方案是用\(dp[v][0]\)表示与v相连的联通块大小大于等于k的所有方案数之和，这样对于切断(u, v)的情况，直接\(dp[u][i] = dp[u][i] * dp[v][0]\)即可，前提是在这一步之前\(dp[u][i]\)没有更新过。所以我们接下来让更小的i中的“不切断的情况”来更新这里的\(dp[u][i]\)。这里直接\(dp[u][i + j] += dp[u][i] * dp[v][j]\)是没有问题的。

啊对了！这个代码看起来是\(O(n^3)\)的啊！

……但其实由于每次两层循环i、j分别枚举了子树u（的已知部分）和子树v的点，时间复杂度增加了sze[u] * sze[v]，相当于枚举了每一对点，那么总计每一对点只被枚举了一次。总计\(O(n^2)\)。

代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef unsigned long long ll;
#define INF 0x3f3f3f3f
#define enter putchar('\n')
#define space putchar(' ')
template <class T>
bool read(T &x){
    char c;
    bool op = 0;
    while(c = getchar(), c < '0' || c > '9')
	if(c == '-') op = 1;
	else if(c == EOF) return 0;
    x = c - '0';
    while(c = getchar(), c >= '0' && c <= '9')
	x = x * 10 + c - '0';
    if(op) x = -x;
    return 1;
}
template <class T>
void write(T x){
    if(x >= 10) write(x / 10);
    putchar('0' + x % 10);
}
const int N = 2005, P = 1e9+7;
int n, k, sze[N];
int ecnt, adj[N], nxt[2*N], go[2*N];
ll dp[N][N], ans;
void add(int u, int v){
    go[++ecnt] = v;
    nxt[ecnt] = adj[u];
    adj[u] = ecnt;
}
void dfs(int u, int pre){
    dp[u][1] = sze[u] = 1;
    for(int v, e = adj[u]; e; e = nxt[e])
        if(v = go[e], v != pre){
            dfs(v, u);
            for(int i = sze[u]; i; i--){
                for(int j = 1; j <= sze[v]; j++)
                    dp[u][i + j] = (dp[u][i + j] + dp[v][j] * dp[u][i]) % P;
                dp[u][i] = dp[u][i] * dp[v][0] % P;
            }
            sze[u] += sze[v];
        }
    for(int i = k; i <= sze[u]; i++)
        dp[u][0] = (dp[u][0] + dp[u][i]) % P;
}
int main(){
    read(n), read(k);
    for(int i = 1, u, v; i < n; i++)
        read(u), read(v), add(u, v), add(v, u);
    dfs(1, 0);
    for(int i = k; i <= n; i++)
        ans = (ans + dp[1][i]) % P;
    write(ans), enter;
    return 0;
}