[Noi2014]购票 斜率优化DP+可持久化凸包

貌似网上大部分题解都是CDQ分治+点分治然后再斜率优化DP，我貌似并没有用这个方法。

这一题跟这题有点像，只不过多了一个l的限制

如果说直接跑斜率优化DP，存储整个序列的话，显然是不行的，如图所示（图鸣谢某巨佬）

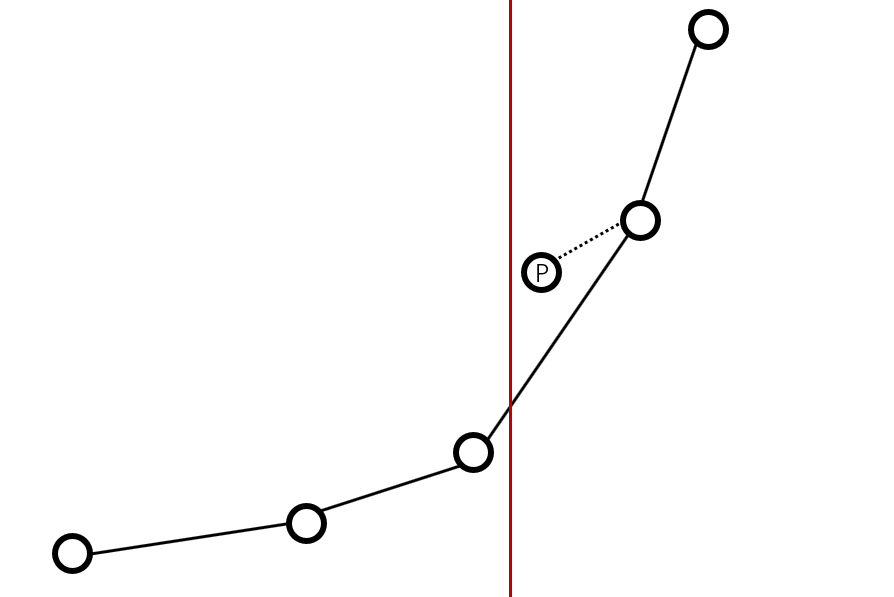
所以我们需要种一棵线段树，每个线段树内存储一个存当前区间凸包的单调栈，弹出插入操作跟刚刚说的那题一样。

查询的话就查询下整个区间中所有凸包上的最大值就可以了。

时间复杂度：$O(n\log^2\ n)$。写起来并不算很困难。

 #include<bits/stdc++.h>
 #define M 200005
 #define L long long
 #define INF (1LL<<62)
 using namespace std;

 struct edge{int u,v,next;}e[M]={}; int head[M]={},use=;
 void add(int x,int y,int z){use++;e[use].u=y;e[use].v=z;e[use].next=head[x];head[x]=use;}
 L D[M]={},P[M]={},Q[M]={},F[M]={},n,t,up[M]={};
 double slope(int i,int j){return .*(F[i]-F[j])/(D[i]-D[j]);}
 L getans(int x,int y){if(y==) return INF; return F[y]+(D[x]-D[y])*P[x]+Q[x];}

 int f[M][]={},dep[M]={};
 int jump(int x,L dis){
     for(int i=;~i;i--)
     if(D[x]-D[f[x][i]]<=dis){
         dis-=D[x]-D[f[x][i]];
         x=f[x][i];
     }
     return max(,dep[x]);
 }

 struct tb{
     int *q,l,r;
     tb(){l=; r=; q=NULL;}
     tb(int len){
         q=new int[len+];
         memset(q,,sizeof(int )*(len+));
         l=; r=;
     }
     int add(int x){
         int ll=l,rr=r-;
         if(l<r){
             while(ll<rr){
                 int mid=(ll+rr)>>;
                 if(slope(q[mid],q[mid+])>slope(q[mid+],x)) rr=mid;
                 else ll=mid+;
             }
             if(slope(q[ll],q[ll+])<slope(q[ll+],x)) ll++;
             r=ll;
         }
         int res=q[++r]; q[r]=x;
         return res;
     }
     L getans(int x){
         int ll=l,rr=r-;
         if(l>=r) return q[l];
         while(ll<rr){
             int mid=(ll+rr+)>>;
             if(slope(q[mid],q[mid+])<P[x]) ll=mid;
             else rr=mid-;
         }
         if(slope(q[ll],q[ll+])<P[x])
         return q[ll+];
         return q[ll];
     }
 };

 struct node{int l,r;tb a;}a[M*];
 void build(int x,int l,int r){
     a[x].l=l; a[x].r=r;
     a[x].a=tb(r-l+);
     if(l==r) return; int mid=(l+r)>>;
     build(x<<,l,mid); build(x<<|,mid+,r);
 }
 void updata(int x,int k,int id,int lastL[],int lastR[],int lastT[]){
     lastL[]=a[x].a.l; lastR[]=a[x].a.r;
     lastT[]=a[x].a.add(id);
     if(a[x].l==a[x].r) return; int mid=(a[x].l+a[x].r)>>;
     if(k<=mid) updata(x<<,k,id,lastL+,lastR+,lastT+);
     else updata(x<<|,k,id,lastL+,lastR+,lastT+);
 }
 void reset(int x,int k,int lastL[],int lastR[],int lastT[]){
     a[x].a.q[a[x].a.r]=lastT[];
     a[x].a.l=lastL[]; a[x].a.r=lastR[];
     if(a[x].l==a[x].r) return; int mid=(a[x].l+a[x].r)>>;
     if(k<=mid) reset(x<<,k,lastL+,lastR+,lastT+);
     else reset(x<<|,k,lastL+,lastR+,lastT+);
 }
 L query(int x,int l,int r,int k){
     if(l<=a[x].l&&a[x].r<=r)
     return getans(k,a[x].a.getans(k));
     L mid=(a[x].l+a[x].r)>>,minn=INF;
     if(l<=mid) minn=min(minn,query(x<<,l,r,k));
     if(mid<r) minn=min(minn,query(x<<|,l,r,k));
     return minn;
 }

 void dfs(int x,int fa,L Dis){
     f[x][]=fa; dep[x]=dep[fa]+; D[x]=Dis;
     for(int i=;i<;i++) f[x][i]=f[f[x][i-]][i-];
     int y=jump(x,up[x]);
     F[x]=query(,y,dep[x],x);
     int lastL[]={},lastR[]={},lastT[]={};
     updata(,dep[x],x,lastL,lastR,lastT);
     for(int i=head[x];i;i=e[i].next) dfs(e[i].u,x,Dis+e[i].v);
     reset(,dep[x],lastL,lastR,lastT);
 }
 int main(){
     scanf("%d%d",&n,&t);
     for(int i=;i<=n;i++){
         L fa,dis; scanf("%lld%lld%lld%lld%lld",&fa,&dis,P+i,Q+i,up+i);
         add(fa,i,dis);
     }
     build(,,n);
     int hh[]; updata(,,,hh,hh,hh);
     dep[]=; D[]=-INF;
     for(int i=head[];i;i=e[i].next) dfs(e[i].u,,e[i].v);
     for(int i=;i<=n;i++) printf("%lld\n",F[i]);
 }