算法:图(Graph)的遍历、最小生成树和拓扑排序
背景
不同的数据结构有不同的用途,像:数组、链表、队列、栈多数是用来做为基本的工具使用,二叉树多用来作为已排序元素列表的存储,B 树用在存储中,本文介绍的 Graph 多数是为了解决现实问题(说到底,所有的数据结构都是这个目的),如:网络布局、任务安排等。
图的基本概念
示例
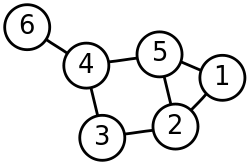
顶点(Vertex)
上图的 1、2、3、4、5、6 就是顶点。
邻接(Adjoin)
如果 A 和 B 通过定向边相连,且方向为 A -> B,则 B 为 A 的邻接,如果相连的边是没有方向的,则 A 和 B 互为邻接。
边(Edge)
顶点之间的连线就是边。
连通图(Connected Graph)
不考虑边的方向性,从任何一个节点都可以遍历到其它节点。本文的所有算法(除了拓扑排序)只适合连通图。
定向图(Directed Graph)
图中的所有边都带方向。
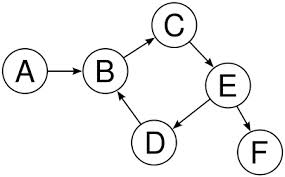
权重图(Weighted Graph)
图中的所有边都有权重。
图的程序表示
如果图 T 有 A、B、C 三个节点,有 A -> B,B -> C,C -> A 三个边(没有方向),如何在程序中表示 T 呢?
邻接矩阵
A B C
A 0 1 0
B 0 0 1
C 1 0 0
矩阵的行代表了定向边的起始顶点,矩阵的列代表了定向边的介绍顶点,矩阵中的值:1 代表了列是行的邻接,0 则反之。如果边没有方向,则矩阵是相对于正对角线是对称的。
邻接列表
A:[ B ]
B:[ C ]
C:[ A ]
这个就不多说了,多数书籍使用都是邻接矩阵。
代码
class Vertex<T>
{
public T Value { get; set; } public bool WasVisited { get; set; }
} class Graph<T>
{
#region 私有字段 private int _maxSize;
private Vertex<T>[] _vertexs;
private bool[][] _edges;
private int _vertexCount = ; #endregion #region 构造方法 public Graph(int maxSize)
{
_maxSize = maxSize;
_vertexs = new Vertex<T>[_maxSize];
_edges = new bool[_maxSize][];
for (var i = ; i < _maxSize; i++)
{
_edges[i] = new bool[_maxSize];
}
} #endregion #region 添加顶点 public Graph<T> AddVertex(T value)
{
_vertexs[_vertexCount++] = new Vertex<T> { Value = value }; return this;
} #endregion #region 添加边 public Graph<T> AddUnDirectedEdge(T startItem, T endItem)
{
var startIndex = this.GetVertexIndex(startItem);
var endIndex = this.GetVertexIndex(endItem); _edges[startIndex][endIndex] = true;
_edges[endIndex][startIndex] = true; return this;
} public Graph<T> AddDirectedEdge(T startItem, T endItem)
{
var startIndex = this.GetVertexIndex(startItem);
var endIndex = this.GetVertexIndex(endItem); _edges[startIndex][endIndex] = true; return this;
} #endregion
}
图的常见算法
遍历
本文的遍历算法只适合一般的无向图。
深度优先遍历
深度优先遍历的原则是:尽可能的离开始节点远,二叉树的三种遍历算法都属于这种算法。
示例

从 A 开始的遍历顺序为(邻接的遍历顺序为字母升序):ABCEDBF。
栈版本
#region 深度优先遍历:栈版本
public void DepthFirstSearch(T startItem, Action<T> action)
{
var startIndex = this.GetVertexIndex(startItem);
var stack = new Stack<int>();
this.DepthFirstSearchVisit(stack, startIndex, action);
while (stack.Count > )
{
var adjoinVertexIndex = this.GetNextUnVisitedAdjoinVertexIndex(stack.Peek());
if (adjoinVertexIndex >= )
{
this.DepthFirstSearchVisit(stack, adjoinVertexIndex, action);
}
else
{
stack.Pop();
}
}
this.ResetVisited();
}
private void DepthFirstSearchVisit(Stack<int> stack, int index, Action<T> action)
{
_vertexs[index].WasVisited = true;
action(_vertexs[index].Value);
stack.Push(index);
}
#endregion
递归版本
#region 深度优先遍历:递归版本
public void DepthFirstSearchRecursion(T startItem, Action<T> action)
{
var startIndex = this.GetVertexIndex(startItem);
this.DepthFirstSearchRecursionVisit(startIndex, action);
this.ResetVisited();
}
private void DepthFirstSearchRecursionVisit(int index, Action<T> action)
{
_vertexs[index].WasVisited = true;
action(_vertexs[index].Value);
var adjoinVertexIndex = this.GetNextUnVisitedAdjoinVertexIndex(index);
while (adjoinVertexIndex >= )
{
this.DepthFirstSearchRecursionVisit(adjoinVertexIndex, action);
adjoinVertexIndex = this.GetNextUnVisitedAdjoinVertexIndex(index);
}
}
#endregion
广度优先遍历
广度优先遍历的原则是:尽可能的离开始节点近。这个算法没有办法通过递归实现,多数都是使用的队列(终于发现了队列的又一个用处)。
示例

从 A 开始的遍历顺序为(邻接的遍历顺序为字母升序):ABCEDFB。
代码
#region 广度优先遍历
public void BreadthFirstSearch(T startItem, Action<T> action)
{
var startIndex = this.GetVertexIndex(startItem);
var queue = new Queue<int>();
this.BreadthFirstSearchVisit(queue, startIndex, action);
while (queue.Count > )
{
var adjoinVertexIndexs = this.GetNextUnVisitedAdjoinVertexIndexs(queue.Dequeue());
foreach (var adjoinVertexIndex in adjoinVertexIndexs)
{
this.BreadthFirstSearchVisit(queue, adjoinVertexIndex, action);
}
}
this.ResetVisited();
}
private void BreadthFirstSearchVisit(Queue<int> queue, int index, Action<T> action)
{
_vertexs[index].WasVisited = true;
action(_vertexs[index].Value);
queue.Enqueue(index);
}
#endregion
最小生成树
本文的最小生成树算法只适合一般的无向图。
将 N 个顶点连接起来的最小树叫:最小生成树。
给定一个颗有 N 个顶点的连通图,则最小生成树的边为:N - 1。
不同的遍历算法生成的最小生成树是不同的,下面使用广度优先遍历来生成最小树。
示例

从 A 开始的遍历顺序为(邻接的遍历顺序为字母升序):A->B、B->C、C->E、E->D、E->F、D->B。
代码
#region 最小生成树
public void DisplayMinimumSpanningTree(T startItem)
{
var startIndex = this.GetVertexIndex(startItem);
var queue = new Queue<int>();
_vertexs[startIndex].WasVisited = true;
queue.Enqueue(startIndex);
while (queue.Count > )
{
var currentIndex = queue.Dequeue();
var adjoinVertexIndexs = this.GetNextUnVisitedAdjoinVertexIndexs(currentIndex);
foreach (var adjoinVertexIndex in adjoinVertexIndexs)
{
Console.WriteLine(_vertexs[currentIndex].Value + "->" + _vertexs[adjoinVertexIndex].Value);
_vertexs[adjoinVertexIndex].WasVisited = true;
queue.Enqueue(adjoinVertexIndex);
}
}
this.ResetVisited();
}
#endregion
拓扑排序
拓扑排序只适合定向图,且图中不存在循环结构。其算法非常简单,依次获取图中的没有邻接顶点的顶点,然后删除该顶点。
示例

上图出现了循环结构,假如没有顶点 C,拓扑排序的结果为(顶点的遍历顺序为字母升序):EFDAB。
算法
#region 拓扑排序
public List<T> TopologySort()
{
var cloneVertexs = (Vertex<T>[])_vertexs.Clone();
var cloneEdges = (bool[][])_edges.Clone();
var cloneVertexCount = _vertexCount;
var results = new List<T>();
while (_vertexCount > )
{
var successor = this.NextSuccessor();
if (successor == -)
{
throw new InvalidOperationException("出现循环了!");
}
results.Insert(, _vertexs[successor].Value);
this.RemoveVertex(successor);
_vertexCount--;
}
_vertexs = cloneVertexs;
_edges = cloneEdges;
_vertexCount = cloneVertexCount;
return results;
}
private int NextSuccessor()
{
for (var row = ; row < _vertexCount; row++)
{
if (_edges[row].Take(_vertexCount).All(x => !x))
{
return row;
}
}
return -;
}
private void RemoveVertex(int successor)
{
for (int i = successor; i < _vertexCount - ; i++)
{
_vertexs[i] = _vertexs[i + ];
}
for (int row = successor; row < _vertexCount - ; row++)
{
for (int column = ; column < _vertexCount; column++)
{
_edges[row][column] = _edges[row + ][column];
}
}
for (int column = successor; column < _vertexCount - ; column++)
{
for (int row = ; row < _vertexCount; row++)
{
_edges[row][column] = _edges[row][column + ];
}
}
}
#endregion
完整代码
using System;
using System.Collections.Generic;
using System.Collections.ObjectModel;
using System.Linq;
using System.Text;
using System.Threading.Tasks; namespace DataStuctureStudy.Graphs
{
class GraphTest
{
public static void Test()
{
var graph = new Graph<String>();
graph
.AddVertex("A")
.AddVertex("B")
.AddVertex("C")
.AddVertex("D")
.AddVertex("E")
.AddVertex("F")
.AddVertex("G")
.AddVertex("H")
.AddVertex("I");
graph
.AddDirectedEdge("A", "B").AddDirectedEdge("A", "C").AddDirectedEdge("A", "D").AddDirectedEdge("A", "E")
.AddDirectedEdge("B", "F")
.AddDirectedEdge("D", "G")
.AddDirectedEdge("F", "H")
.AddDirectedEdge("G", "I"); Console.WriteLine("深度遍历,栈版本:");
graph.DepthFirstSearch("A", Console.Write);
Console.WriteLine();
Console.WriteLine(); Console.WriteLine("深度遍历,递归版本:");
graph.DepthFirstSearchRecursion("A", Console.Write);
Console.WriteLine();
Console.WriteLine(); Console.WriteLine("广度遍历:");
graph.BreadthFirstSearch("A", Console.Write);
Console.WriteLine();
Console.WriteLine(); Console.WriteLine("最小生成树:");
graph.DisplayMinimumSpanningTree("A");
Console.WriteLine();
Console.WriteLine(); Console.WriteLine("拓扑排序:");
var results = graph.TopologySort();
Console.WriteLine(String.Join("->", results.ToArray()));
Console.WriteLine();
} class Vertex<T>
{
public T Value { get; set; } public bool WasVisited { get; set; }
} class Graph<T>
{
#region 私有字段 private int _maxSize;
private Vertex<T>[] _vertexs;
private bool[][] _edges;
private int _vertexCount = ; #endregion #region 构造方法 public Graph(int maxSize)
{
_maxSize = maxSize;
_vertexs = new Vertex<T>[_maxSize];
_edges = new bool[_maxSize][];
for (var i = ; i < _maxSize; i++)
{
_edges[i] = new bool[_maxSize];
}
} #endregion #region 添加顶点 public Graph<T> AddVertex(T value)
{
_vertexs[_vertexCount++] = new Vertex<T> { Value = value }; return this;
} #endregion #region 添加边 public Graph<T> AddUnDirectedEdge(T startItem, T endItem)
{
var startIndex = this.GetVertexIndex(startItem);
var endIndex = this.GetVertexIndex(endItem); _edges[startIndex][endIndex] = true;
_edges[endIndex][startIndex] = true; return this;
} public Graph<T> AddDirectedEdge(T startItem, T endItem)
{
var startIndex = this.GetVertexIndex(startItem);
var endIndex = this.GetVertexIndex(endItem); _edges[startIndex][endIndex] = true; return this;
} #endregion #region 深度优先遍历:栈版本 public void DepthFirstSearch(T startItem, Action<T> action)
{
var startIndex = this.GetVertexIndex(startItem);
var stack = new Stack<int>(); this.DepthFirstSearchVisit(stack, startIndex, action);
while (stack.Count > )
{
var adjoinVertexIndex = this.GetNextUnVisitedAdjoinVertexIndex(stack.Peek());
if (adjoinVertexIndex >= )
{
this.DepthFirstSearchVisit(stack, adjoinVertexIndex, action);
}
else
{
stack.Pop();
}
} this.ResetVisited();
} private void DepthFirstSearchVisit(Stack<int> stack, int index, Action<T> action)
{
_vertexs[index].WasVisited = true;
action(_vertexs[index].Value);
stack.Push(index);
} #endregion #region 深度优先遍历:递归版本 public void DepthFirstSearchRecursion(T startItem, Action<T> action)
{
var startIndex = this.GetVertexIndex(startItem); this.DepthFirstSearchRecursionVisit(startIndex, action); this.ResetVisited();
} private void DepthFirstSearchRecursionVisit(int index, Action<T> action)
{
_vertexs[index].WasVisited = true;
action(_vertexs[index].Value); var adjoinVertexIndex = this.GetNextUnVisitedAdjoinVertexIndex(index);
while (adjoinVertexIndex >= )
{
this.DepthFirstSearchRecursionVisit(adjoinVertexIndex, action);
adjoinVertexIndex = this.GetNextUnVisitedAdjoinVertexIndex(index);
}
} #endregion #region 广度优先遍历 public void BreadthFirstSearch(T startItem, Action<T> action)
{
var startIndex = this.GetVertexIndex(startItem);
var queue = new Queue<int>(); this.BreadthFirstSearchVisit(queue, startIndex, action);
while (queue.Count > )
{
var adjoinVertexIndexs = this.GetNextUnVisitedAdjoinVertexIndexs(queue.Dequeue());
foreach (var adjoinVertexIndex in adjoinVertexIndexs)
{
this.BreadthFirstSearchVisit(queue, adjoinVertexIndex, action);
}
} this.ResetVisited();
} private void BreadthFirstSearchVisit(Queue<int> queue, int index, Action<T> action)
{
_vertexs[index].WasVisited = true;
action(_vertexs[index].Value);
queue.Enqueue(index);
} #endregion #region 最小生成树 public void DisplayMinimumSpanningTree(T startItem)
{
var startIndex = this.GetVertexIndex(startItem);
var queue = new Queue<int>(); _vertexs[startIndex].WasVisited = true;
queue.Enqueue(startIndex);
while (queue.Count > )
{
var currentIndex = queue.Dequeue();
var adjoinVertexIndexs = this.GetNextUnVisitedAdjoinVertexIndexs(currentIndex);
foreach (var adjoinVertexIndex in adjoinVertexIndexs)
{
Console.WriteLine(_vertexs[currentIndex].Value + "->" + _vertexs[adjoinVertexIndex].Value); _vertexs[adjoinVertexIndex].WasVisited = true;
queue.Enqueue(adjoinVertexIndex);
}
} this.ResetVisited();
} #endregion #region 拓扑排序 public List<T> TopologySort()
{
var cloneVertexs = (Vertex<T>[])_vertexs.Clone();
var cloneEdges = (bool[][])_edges.Clone();
var cloneVertexCount = _vertexCount; var results = new List<T>();
while (_vertexCount > )
{
var successor = this.NextSuccessor();
if (successor == -)
{
throw new InvalidOperationException("出现循环了!");
} results.Insert(, _vertexs[successor].Value); this.RemoveVertex(successor);
_vertexCount--;
} _vertexs = cloneVertexs;
_edges = cloneEdges;
_vertexCount = cloneVertexCount; return results;
} private int NextSuccessor()
{
for (var row = ; row < _vertexCount; row++)
{
if (_edges[row].Take(_vertexCount).All(x => !x))
{
return row;
}
} return -;
} private void RemoveVertex(int successor)
{
for (int i = successor; i < _vertexCount - ; i++)
{
_vertexs[i] = _vertexs[i + ];
} for (int row = successor; row < _vertexCount - ; row++)
{
for (int column = ; column < _vertexCount; column++)
{
_edges[row][column] = _edges[row + ][column];
}
} for (int column = successor; column < _vertexCount - ; column++)
{
for (int row = ; row < _vertexCount; row++)
{
_edges[row][column] = _edges[row][column + ];
}
}
} #endregion #region 帮助方法 private int GetVertexIndex(T item)
{
for (var i = ; i < _vertexCount; i++)
{
if (_vertexs[i].Value.Equals(item))
{
return i;
}
}
return -;
} private int GetNextUnVisitedAdjoinVertexIndex(int index)
{
for (var i = ; i < _vertexCount; i++)
{
if (_edges[index][i] && _vertexs[i].WasVisited == false)
{
return i;
}
} return -;
} private List<int> GetNextUnVisitedAdjoinVertexIndexs(int index)
{
var results = new List<int>(); for (var i = ; i < _vertexCount; i++)
{
if (_edges[index][i] && _vertexs[i].WasVisited == false)
{
results.Add(i);
}
} return results;
} private void ResetVisited()
{
for (var i = ; i < _vertexCount; i++)
{
_vertexs[i].WasVisited = false;
}
} #endregion
}
}
}
备注
本文没有解释权重图,下篇再介绍。
算法:图(Graph)的遍历、最小生成树和拓扑排序的更多相关文章
- 算法与数据结构(七) AOV网的拓扑排序
今天博客的内容依然与图有关,今天博客的主题是关于拓扑排序的.拓扑排序是基于AOV网的,关于AOV网的概念,我想引用下方这句话来介绍: AOV网:在现代化管理中,人们常用有向图来描述和分析一项工程的计划 ...
- 算法与数据结构(七) AOV网的拓扑排序(Swift版)
今天博客的内容依然与图有关,今天博客的主题是关于拓扑排序的.拓扑排序是基于AOV网的,关于AOV网的概念,我想引用下方这句话来介绍: AOV网:在现代化管理中,人们常用有向图来描述和分析一项工程的计划 ...
- 关于最小生成树,拓扑排序、强连通分量、割点、2-SAT的一点笔记
关于最小生成树,拓扑排序.强连通分量.割点.2-SAT的一点笔记 前言:近期在复习这些东西,就xjb写一点吧.当然以前也写过,但这次偏重不太一样 MST 最小瓶颈路:u到v最大权值最小的路径.在最小生 ...
- 有向无环图的应用—AOV网 和 拓扑排序
有向无环图:无环的有向图,简称 DAG (Directed Acycline Graph) 图. 一个有向图的生成树是一个有向树,一个非连通有向图的若干强连通分量生成若干有向树,这些有向数形成生成森林 ...
- Almost Acyclic Graph CodeForces - 915D (思维+拓扑排序判环)
Almost Acyclic Graph CodeForces - 915D time limit per test 1 second memory limit per test 256 megaby ...
- NX二次开发-算法篇-冒泡排序(例子:遍历所有点并排序)
NX9+VS2012 #include <uf.h> #include <uf_ui.h> #include <uf_curve.h> #include <u ...
- 拓扑排序-有向无环图(DAG, Directed Acyclic Graph)
条件: 1.每个顶点出现且只出现一次. 2.若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面. 有向无环图(DAG)才有拓扑排序,非DAG图没有拓扑排序一说. 一 ...
- 拓扑排序---AOV图
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中全部顶点排成一个线性序列, 使得图中随意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出如 ...
- BFS (1)算法模板 看是否需要分层 (2)拓扑排序——检测编译时的循环依赖 制定有依赖关系的任务的执行顺序 djkstra无非是将bfs模板中的deque修改为heapq
BFS模板,记住这5个: (1)针对树的BFS 1.1 无需分层遍历 from collections import deque def levelOrderTree(root): if not ro ...
随机推荐
- Kubernetes Ingress实战
本节内容: 服务发现与负载均衡 Ingress实战 一.服务发现与负载均衡 在前面的安装部署kubernetes集群中已经简单用示例来演示了Pod和Service,Kubernetes通过Servic ...
- 一步一步学习IdentityServer3 (15) 授权模式那些事
总结一句话,其实很简单 在什么Clients 拿的认证权限Scope 就去 去开什么Scope限制的服务接口门 在写Clients的时候,会有Scope,看下面的代码 new Client { Cli ...
- GUC-7 同步锁 Lock
import java.util.concurrent.locks.Lock; import java.util.concurrent.locks.ReentrantLock; /* * 一.用于解决 ...
- OpenCV处理直方图
直方图可以用来描述各种不同的事物,如物体的色彩分布.物体边缘梯度模板,以及表示目标位置的当前假设. 简单的说,直方图就是对数据进行统计,将统计值组织到一系列事先定义好的bin中.bin中的数值是从数据 ...
- 009 HDFS的shell命令(里面有一个安全模式)
一:dfs的命令 1.所有的领命 2.解释 -appendToFile <localsrc> ... <dst> :追加文件 -checksum <src> . ...
- Ubuntu16.04下Kylin的安装与配置
一.系统环境 kylin的安装配置并不像官方文档中描述的那样简单,复杂的原因在于hadoop,hive,hbase,kylin的版本一定要兼容,不然就会出现各种奇怪的错误.以下各软件版本可以成功运行k ...
- 数据挖掘算法:关联分析二(FP-tree算法)
三.FP-tree算法 下面介绍一种使用了与Apriori完全不同的方法来发现频繁项集的算法FP-tree.FP-tree算法在过程中没有像Apriori一样产生候选集,而是采用了更为紧凑的数据结构组 ...
- MYSQL插入不能中文的问题的解决
这个问题是由于数据库的字符集不对的问题. 解决方法: 打开要用的数据库,输入命令 status 如果Client characterset 值为utf8,则要改为:set char set 'gbk' ...
- linux通过c++实现线程池类
目录 线程池的实现 线程池已基于C++11重写 : 基于C++11实现线程池的工作原理 前言 线程池的概念 使用原因及适用场合 线程池的实现原理 程序测试 线程池的实现 线程池已基于C++11重写 : ...
- 将已有的项目提交到GitHub
1.目的: 将已有的项目提交到GitHub 2.准备工作 2.1 此教程建立在对git有初步的理解上 2.2 此教程之前需准备工作 a.熟悉git的一些基本命令和原理. b.已注册有GitHub账号. ...
