<泛> 并查集

最近写这些东西呢，主要是整理一下知识，自己写一遍，看看还是不是我的。

原理与实践相结合，缺一不可

背景

有时候，给你一张很复杂的关系网络图，如果关系具有传递性，那么，我们该如何处理这些关系集合。

一个很简单的例子就是，大学里面有很多人，如果我们获取到他们两两之间的相识关系，如果相识关系具备可传递性，那么，很多信息需要求解：

·任意两个人拉出来，他们是否认识呢，如果群体很庞大，我们该如何求解该问题·

·所有这些人总共可以分为多少个集合呢，怎么求解呢

等等等等

我们今天用一个数据结构来解决这些问题，或者说，用并查集来维护这些信息

思想

我们用树结构来实现，如果两个人认识，我们就创建两个树结点代表之，且任指一个结点作为另一个结点的父节点，我们把所有的两两关系均如此做，就可以得到一棵关系树。

如：r 认识 z，z 认识 q，那么r 可以通过 z 认识 q，在树结构上同样如此，树表示为一棵单支树，r——z——q

但是，如果数量很大的话，这棵树将会有很多层，如果要解决第一个问题，我们还需要遍历整棵树才能得到答案，还是很费时间

那么我们采用路径压缩的方法来解决，即：   r

/    \　

z       q

我们把q也挂在z的父亲下面，所有的结点都如此做，如果两个人所指向的根（父）结点是同一个，那么两个人在一个集合中，此查询复杂度为O(1)

我们来解决第二个问题，一共可以构成多少个关系网（集合），我们最开始设置每个节点的根节点为自己，经过上述处理后，我们只需要检查一下有多少个节点的根节点为自己，说明就有多少张关系网。 此查询复杂度为：  O(n)

泛型代码：

//Union_Find.h

#pragma once
#include <map>

template<typename value_type>
class Union_Find
{
public:
    Union_Find();
    value_type find(const value_type&);
    void unite(value_type, value_type);
    int set_cnt()const;                   //总共的构成的集合个数
    bool same(const value_type&, const value_type&);

private:
    void _clear();
    void _init(const value_type&);

private:
    std::map<value_type, value_type> _parent;
    std::map<value_type, int> _rank;                 //记录树的高度
};

template<typename value_type>
Union_Find<value_type>::Union_Find()
{
    _clear();
}

template<typename value_type>
void Union_Find<value_type>::_clear()
{
    _parent.clear();
    _rank.clear();
}

template<typename value_type>
value_type Union_Find<value_type>::find(const value_type& item)
{
    if (_parent[item] == item) return item;
    return _parent[item] = find(_parent[item]);   //![1] 顺便 实现 路径压缩
}

template<typename value_type>
void Union_Find<value_type>::unite(value_type lhs, value_type rhs)
{
    _init(lhs), _init(rhs);

    lhs = _parent[lhs];
    rhs = _parent[rhs];
    if (lhs == rhs)return;

    //![2] 合并两棵树，其实可以直接把右挂在左树上，或反之，但是为了使合并后的整棵树的高度最低，我们选择将rank小的向rank大的连边
    //[1]和[2] 的双重优化之下，我们的并查集效率就会非常高了，可以达到O(α(n))的时间复杂度α(n)为Ackermann(阿克曼)函数的反函数，效率比O(log(n))还快
    if (_rank[lhs] < _rank[rhs])    _parent[lhs] = rhs;
    else
    {
        _parent[rhs] = lhs;
        if (_rank[lhs] == _rank[rhs])    _rank[lhs]++;
    }
}

template<typename value_type>
void Union_Find<value_type>::_init(const value_type& item)
{
    if (_parent[item] == value_type())_parent[item] = item;         //如果没有映射，设为自己
}

template<typename value_type>
bool Union_Find<value_type>::same(const value_type& lhs, const value_type& rhs)
{
    return find(lhs) == find(rhs);
}

template<typename value_type>
int Union_Find<value_type>::set_cnt()const
{
    int cnt{  };
    for (auto it : _parent)
        if (it.first == it.second)cnt++;
    return cnt;
}

测试与使用：

#include"E:\数据结构\Union_Find.h"
#include <iostream>
#include <string>
using namespace std;

int main()
{
    Union_Find<string> Ufind;
    string lhs, rhs;
    cout << "请输入关系网络图：" << endl;
    while (cin >> lhs >> rhs, lhs != "null")
        Ufind.unite(lhs, rhs);

    while (cin >> lhs >> rhs, lhs != "null")
        if (Ufind.same(lhs, rhs))cout << lhs << " 和 " << rhs << " 认识" << endl;
        else cout << lhs << " 和 " << rhs << " 不认识" << endl;
        cout << endl << "该程序一共有" << Ufind.set_cnt() << "关系圈子" << endl;
}

结果

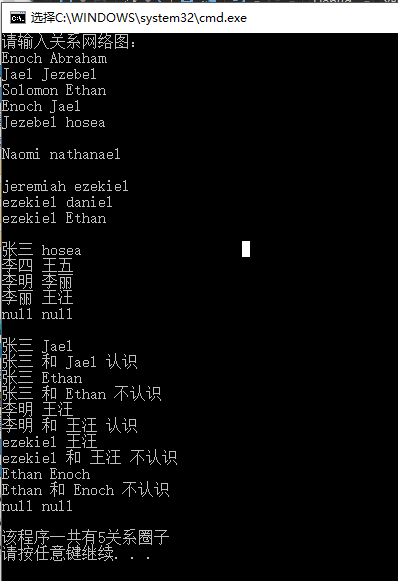
感谢您的阅读，生活愉快~